3D-Computergrafik

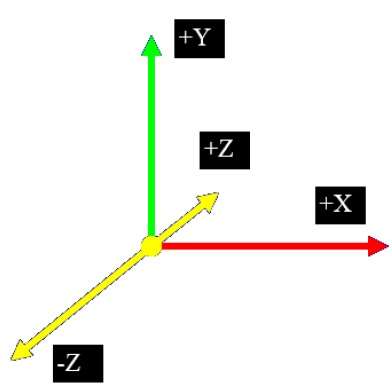
Im 2D-System verwenden wir nur zwei Koordinaten X und Y, in 3D wird jedoch eine zusätzliche Koordinate Z hinzugefügt. 3D-Grafiktechniken und ihre Anwendung sind für die Unterhaltungs-, Spiele- und computergestützte Designbranche von grundlegender Bedeutung. Es ist ein fortlaufendes Forschungsgebiet in der wissenschaftlichen Visualisierung.

Darüber hinaus sind 3D-Grafikkomponenten mittlerweile Teil fast jedes PCs und werden, obwohl sie traditionell für grafikintensive Software wie Spiele gedacht sind, zunehmend von anderen Anwendungen verwendet.

Parallele Projektion

Parallele Projektion verwirft Z-Koordinaten und parallele Linien von jedem Scheitelpunkt auf dem Objekt werden verlängert, bis sie die Ansichtsebene schneiden. Bei der Parallelprojektion geben wir eine Projektionsrichtung anstelle des Projektionszentrums an.

Bei der Parallelprojektion ist der Abstand vom Projektionszentrum zur Projektebene unendlich. Bei dieser Art der Projektion verbinden wir die projizierten Scheitelpunkte durch Liniensegmente, die Verbindungen auf dem ursprünglichen Objekt entsprechen.

Parallele Projektionen sind weniger realistisch, eignen sich jedoch für genaue Messungen. Bei dieser Art von Projektionen bleiben parallele Linien parallel und Winkel bleiben nicht erhalten. In der folgenden Hierarchie werden verschiedene Arten von parallelen Projektionen gezeigt.

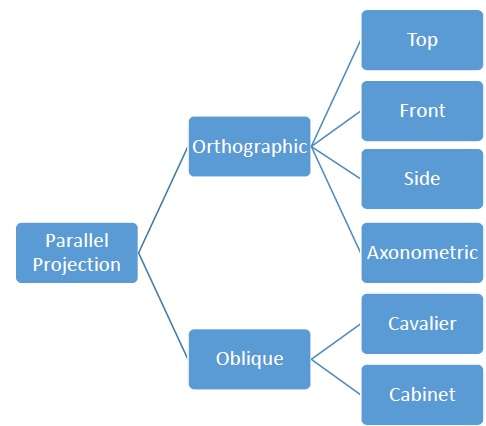
Orthographische Projektion

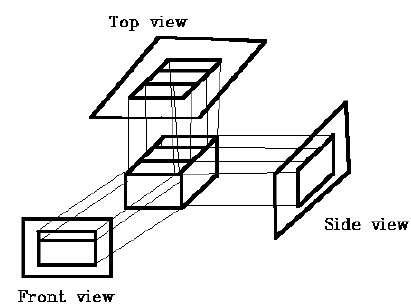
Bei der orthografischen Projektion ist die Projektionsrichtung normal zur Projektion der Ebene. Es gibt drei Arten von orthografischen Projektionen:

• Frontprojektion
• Top Projektion
• Seitenprojektion

Schrägprojektion

Bei der Schrägprojektion ist die Projektionsrichtung nicht normal zur Projektion der Ebene. Bei der Schrägprojektion können wir das Objekt besser betrachten als bei der orthografischen Projektion.

Es gibt zwei Arten von schrägen Projektionen - Cavalier und Cabinet. Die Cavalier-Projektion bildet mit der Projektionsebene einen Winkel von 45 °. Die Projektion einer Linie senkrecht zur Ansichtsebene hat die gleiche Länge wie die Linie selbst in der Cavalier-Projektion. In einer Kavalierprojektion sind die Verkürzungsfaktoren für alle drei Hauptrichtungen gleich.

Die Schrankprojektion bildet mit der Projektionsebene einen Winkel von 63,4 °. Bei der Schrankprojektion werden Linien senkrecht zur Betrachtungsfläche auf die Hälfte ihrer tatsächlichen Länge projiziert. Beide Projektionen sind in der folgenden Abbildung dargestellt -

Isometrische Projektionen

Orthographische Projektionen, die mehr als eine Seite eines Objekts zeigen, werden aufgerufen axonometric orthographic projections. Die häufigste axonometrische Projektion ist eineisometric projectionwobei die Projektionsebene jede Koordinatenachse im Modellkoordinatensystem in gleichem Abstand schneidet. In dieser Projektion bleibt die Parallelität der Linien erhalten, die Winkel jedoch nicht. Die folgende Abbildung zeigt die isometrische Projektion -

Perspektivische Projektion

Bei der perspektivischen Projektion ist der Abstand vom Projektionszentrum zur Projektebene endlich und die Größe des Objekts ändert sich umgekehrt zum Abstand, der realistischer aussieht.

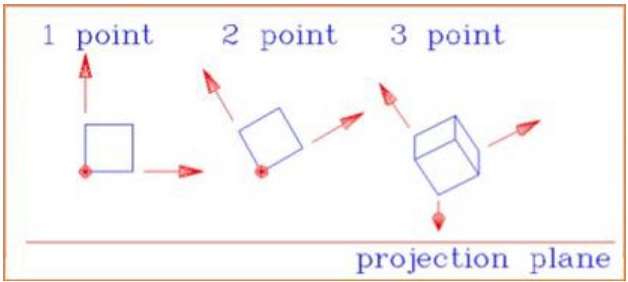
Der Abstand und die Winkel bleiben nicht erhalten und parallele Linien bleiben nicht parallel. Stattdessen konvergieren sie alle an einem einzigen Punkt, der aufgerufen wirdcenter of projection oder projection reference point. Es gibt 3 Arten von perspektivischen Projektionen, die in der folgenden Tabelle dargestellt sind.

• One point Perspektivische Projektion ist einfach zu zeichnen.

• Two point Die perspektivische Projektion vermittelt einen besseren Eindruck von der Tiefe.

• Three point Perspektivische Projektion ist am schwierigsten zu zeichnen.

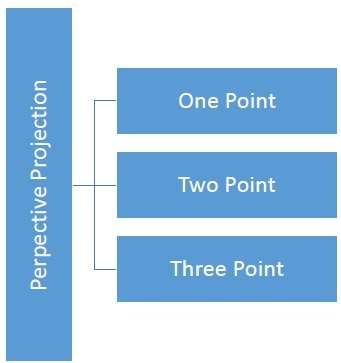
Die folgende Abbildung zeigt alle drei Arten der perspektivischen Projektion -

Übersetzung

Bei der 3D-Übersetzung übertragen wir die Z-Koordinate zusammen mit den X- und Y-Koordinaten. Der Prozess für die Übersetzung in 3D ähnelt der 2D-Übersetzung. Eine Übersetzung verschiebt ein Objekt an eine andere Position auf dem Bildschirm.

Die folgende Abbildung zeigt den Effekt der Übersetzung -

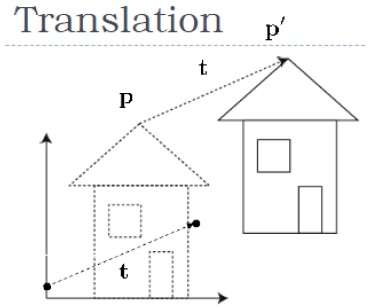
Ein Punkt kann in 3D übersetzt werden, indem der ursprünglichen Koordinate (X, Y, Z) die Übersetzungskoordinate $ (t_ {x,} t_ {y,} t_ {z}) $ hinzugefügt wird, um die neue Koordinate (X ', Y) zu erhalten ', Z').

$ T = \ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ t_ {x} & t_ {y} & t_ {z} & 1 \\ \ end {bmatrix} $

P '= P ∙ T.

$ [X '\: \: Y' \: \: Z '\: \: 1] \: = \: [X \: \: Y \: \: Z \: \: 1] \: \ begin { bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ t_ {x} & t_ {y} & t_ {z} & 1 \\ \ end {bmatrix} $

$ = [X + t_ {x} \: \: \: Y + t_ {y} \: \: \: Z + t_ {z} \: \: \: 1] $