Anzeigen & Ausschneiden
Die Hauptanwendung des Ausschnitts in Computergrafiken besteht darin, Objekte, Linien oder Liniensegmente zu entfernen, die sich außerhalb des Anzeigebereichs befinden. Die Betrachtungstransformation ist unempfindlich gegenüber der Position von Punkten relativ zum Betrachtungsvolumen - insbesondere den Punkten hinter dem Betrachter - und es ist erforderlich, diese Punkte vor dem Generieren der Ansicht zu entfernen.
Punktausschnitt
Das Ausschneiden eines Punktes aus einem bestimmten Fenster ist sehr einfach. Betrachten Sie die folgende Abbildung, in der das Rechteck das Fenster angibt. Das Abschneiden von Punkten gibt an, ob der angegebene Punkt (X, Y) innerhalb des angegebenen Fensters liegt oder nicht. und entscheidet, ob wir die minimalen und maximalen Koordinaten des Fensters verwenden.
Die X-Koordinate des gegebenen Punktes liegt innerhalb des Fensters, wenn X zwischen Wx1 ≤ X ≤ Wx2 liegt. Ebenso befindet sich die Y-Koordinate des angegebenen Punkts innerhalb des Fensters, wenn Y zwischen Wy1 ≤ Y ≤ Wy2 liegt.

Zeilenausschnitt
Das Konzept des Linienschneidens ist dasselbe wie das Punktschneiden. Beim Beschneiden von Linien schneiden wir den Teil der Linie, der sich außerhalb des Fensters befindet, und behalten nur den Teil bei, der sich innerhalb des Fensters befindet.
Cohen-Sutherland-Linienausschnitte
Dieser Algorithmus verwendet das Beschneidungsfenster wie in der folgenden Abbildung gezeigt. Die minimale Koordinate für den Beschneidungsbereich ist $ (XW_ {min,} YW_ {min}) $ und die maximale Koordinate für den Beschneidungsbereich ist $ (XW_ {max,} YW_ {max}) $.
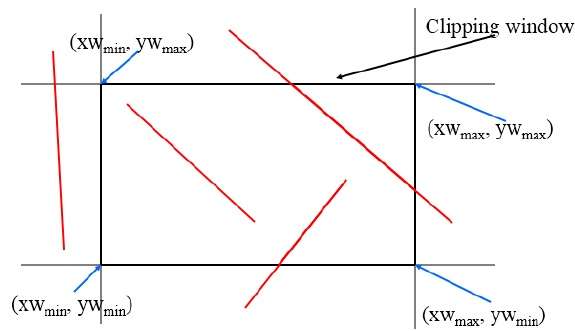
Wir werden 4-Bit verwenden, um die gesamte Region zu teilen. Diese 4 Bits repräsentieren den oberen, unteren, rechten und linken Bereich der Region, wie in der folgenden Abbildung gezeigt. Hier dieTOP und LEFT Bit wird auf 1 gesetzt, weil es das ist TOP-LEFT Ecke.
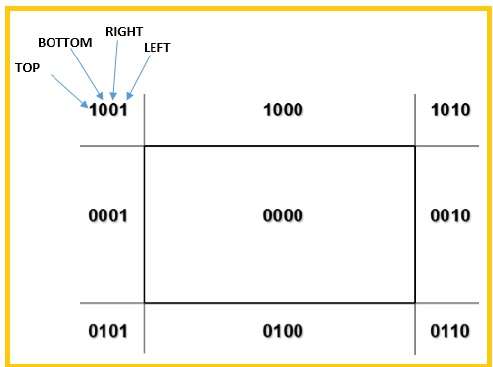
Es gibt 3 Möglichkeiten für die Linie -
Die Linie kann sich vollständig im Fenster befinden (Diese Linie sollte akzeptiert werden).
Die Linie kann sich vollständig außerhalb des Fensters befinden (Diese Linie wird vollständig aus der Region entfernt).
Die Linie kann sich teilweise innerhalb des Fensters befinden (wir finden den Schnittpunkt und zeichnen nur den Teil der Linie, der sich innerhalb des Bereichs befindet).
Algorithmus
Step 1 - Weisen Sie jedem Endpunkt einen Regionalcode zu.
Step 2 - Wenn beide Endpunkte einen Regionalcode haben 0000 dann akzeptiere diese Zeile.
Step 3 - Andernfalls führen Sie die logische ANDBetrieb für beide Regionalcodes.
Step 3.1 - Wenn das Ergebnis nicht ist 0000, dann lehnen Sie die Zeile ab.
Step 3.2 - Sonst brauchst du Clipping.
Step 3.2.1 - Wählen Sie einen Endpunkt der Linie außerhalb des Fensters.
Step 3.2.2 - Suchen Sie den Schnittpunkt an der Fenstergrenze (basierend auf dem Regionalcode).
Step 3.2.3 - Ersetzen Sie den Endpunkt durch den Schnittpunkt und aktualisieren Sie den Regionalcode.
Step 3.2.4 - Wiederholen Sie Schritt 2, bis Sie eine abgeschnittene Zeile finden, die entweder trivial akzeptiert oder trivial abgelehnt wurde.
Step 4 - Wiederholen Sie Schritt 1 für andere Zeilen.
Cyrus-Beck-Zeilenbeschneidungsalgorithmus
Dieser Algorithmus ist effizienter als der Cohen-Sutherland-Algorithmus. Es verwendet eine parametrische Liniendarstellung und einfache Punktprodukte.
Die parametrische Liniengleichung lautet -
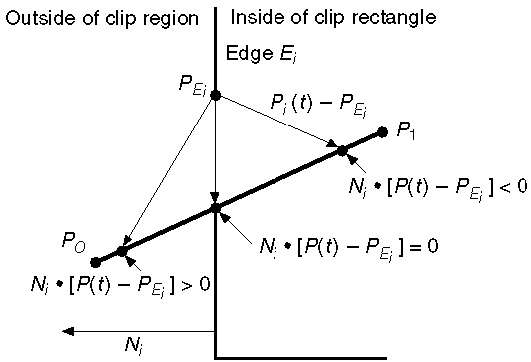
P0P1:P(t) = P0 + t(P1 - P0)Sei N i die äußere Normalkante E i . Wählen Sie nun einen beliebigen Punkt P Ei an der Kante E i und dann das Punktprodukt N i . [P (t) - P Ei ] bestimmt, ob der Punkt P (t) „innerhalb der Clipkante“ oder „außerhalb“ der Clipkante oder liegt "An" der Clipkante.
Der Punkt P (t) liegt innerhalb, wenn N i . [P (t) - P Ei ] <0 ist
Der Punkt P (t) liegt außerhalb, wenn N i . [P (t) - P Ei ]> 0 ist
Der Punkt P (t) liegt am Rand, wenn N i . [P (t) - P Ei ] = 0 (Schnittpunkt)
N i . [P (t) - P Ei ] = 0
N i . [P 0 + t (P 1 - P 0 ) - P Ei ] = 0 (Ersetzen von P (t) durch P 0 + t (P 1 - P 0 ))
N i . [P 0 - P Ei ] + N i. T [P 1 - P 0 ] = 0
N i . [P 0 - P Ei ] + N i ∙ tD = 0 (Ersetzen von [P 1 - P 0 ] durch D )
N i . [P 0 - P Ei ] = - N i ∙ tD
Die Gleichung für t wird,
$$ t = \ tfrac {N_ {i}. [P_ {o} - P_ {Ei}]} {{- N_ {i} .D}} $$
Es gilt für folgende Bedingungen:
- N i ≠ 0 (Fehler kann nicht auftreten)
- D ≤ 0 (P 1 ≤ P 0 )
- N i ∙ D ≠ 0 (P 0 P 1 nicht parallel zu E i )
Polygon-Clipping (Sutherland-Hodgman-Algorithmus)
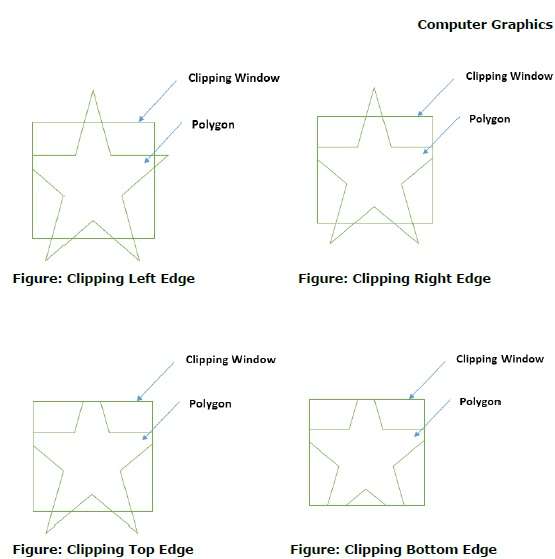
Ein Polygon kann auch durch Angabe des Beschneidungsfensters abgeschnitten werden. Der Sutherland Hodgeman-Polygon-Clipping-Algorithmus wird für das Polygon-Clipping verwendet. Bei diesem Algorithmus werden alle Scheitelpunkte des Polygons gegen jede Kante des Beschneidungsfensters abgeschnitten.
Zuerst wird das Polygon gegen den linken Rand des Polygonfensters abgeschnitten, um neue Scheitelpunkte des Polygons zu erhalten. Diese neuen Scheitelpunkte werden verwendet, um das Polygon gegen die rechte Kante, die obere Kante und die untere Kante des Beschneidungsfensters zu schneiden, wie in der folgenden Abbildung gezeigt.
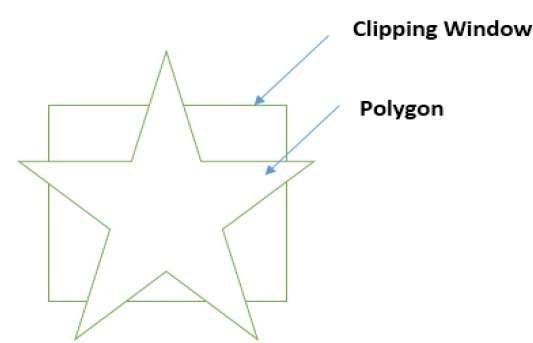
Während der Verarbeitung einer Kante eines Polygons mit einem Beschneidungsfenster wird ein Schnittpunkt gefunden, wenn sich die Kante nicht vollständig innerhalb des Beschneidungsfensters befindet und eine Teilkante vom Schnittpunkt zur Außenkante abgeschnitten wird. Die folgenden Abbildungen zeigen Ausschnitte am linken, rechten, oberen und unteren Rand -
Textausschnitt
Verschiedene Techniken werden verwendet, um Textausschnitte in einer Computergrafik bereitzustellen. Dies hängt von den Methoden zum Generieren von Zeichen und den Anforderungen einer bestimmten Anwendung ab. Es gibt drei Methoden zum Ausschneiden von Text, die unten aufgeführt sind:
- Alle oder keine String-Clipping
- Alle oder keine Zeichenausschnitte
- Textausschnitt
Die folgende Abbildung zeigt das Beschneiden aller oder keiner Zeichenfolgen -
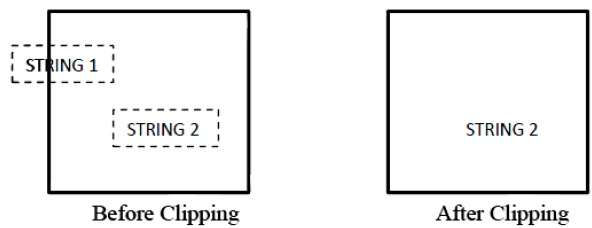
Bei der Beschneidungsmethode für alle oder keine Zeichenfolgen behalten wir entweder die gesamte Zeichenfolge bei oder lehnen die gesamte Zeichenfolge basierend auf dem Beschneidungsfenster ab. Wie in der obigen Abbildung gezeigt, befindet sich STRING2 vollständig im Beschneidungsfenster, sodass wir es behalten und STRING1 nur teilweise im Fenster ist, was wir ablehnen.
Die folgende Abbildung zeigt alle oder keine Zeichenausschnitte -
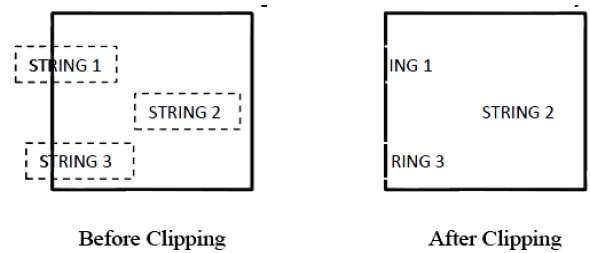
Diese Beschneidungsmethode basiert eher auf Zeichen als auf der gesamten Zeichenfolge. Wenn sich die Zeichenfolge bei dieser Methode vollständig im Beschneidungsfenster befindet, behalten wir sie bei. Wenn es sich teilweise außerhalb des Fensters befindet, dann -
Sie lehnen nur den Teil der Zeichenfolge ab, der sich außerhalb befindet
Befindet sich das Zeichen an der Grenze des Beschneidungsfensters, verwerfen wir das gesamte Zeichen und behalten die restliche Zeichenfolge bei.
Die folgende Abbildung zeigt Textausschnitte -
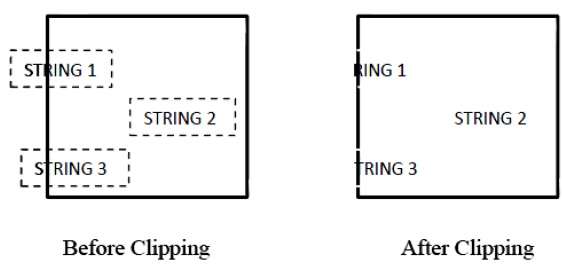
Diese Beschneidungsmethode basiert eher auf Zeichen als auf der gesamten Zeichenfolge. Wenn sich die Zeichenfolge bei dieser Methode vollständig im Beschneidungsfenster befindet, behalten wir sie bei. Wenn es sich teilweise außerhalb des Fensters befindet, dann
Sie lehnen nur den Teil der Zeichenfolge ab, der sich außerhalb befindet.
Befindet sich das Zeichen an der Grenze des Beschneidungsfensters, verwerfen wir nur den Teil des Zeichens, der sich außerhalb des Beschneidungsfensters befindet.
Bitmap-Grafiken
Eine Bitmap ist eine Sammlung von Pixeln, die ein Bild beschreiben. Es handelt sich um eine Art Computergrafik, mit der der Computer Bilder speichert und anzeigt. Bei dieser Art von Grafiken werden Bilder Stück für Stück gespeichert und daher als Bitmap-Grafik bezeichnet. Betrachten wir zum besseren Verständnis das folgende Beispiel, in dem wir ein Smiley mit Bitmap-Grafiken zeichnen.

Jetzt werden wir sehen, wie dieses Smiley-Gesicht Stück für Stück in der Computergrafik gespeichert wird.
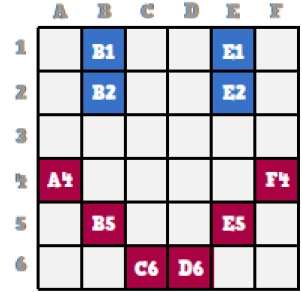
Wenn wir das ursprüngliche Smiley-Gesicht genau betrachten, können wir sehen, dass es zwei blaue Linien gibt, die in der obigen Abbildung als B1, B2 und E1, E2 dargestellt sind.
Auf die gleiche Weise wird der Smiley unter Verwendung der Kombinationsbits von A4, B5, C6, D6, E5 bzw. F4 dargestellt.
Die Hauptnachteile von Bitmap-Grafiken sind -
Wir können die Größe des Bitmap-Bildes nicht ändern. Wenn Sie versuchen, die Größe zu ändern, werden die Pixel unscharf.
Farbige Bitmaps können sehr groß sein.