Zeilengenerierungsalgorithmus

Eine Linie verbindet zwei Punkte. Es ist ein Grundelement in Grafiken. Um eine Linie zu zeichnen, benötigen Sie zwei Punkte, zwischen denen Sie eine Linie zeichnen können. In den folgenden drei Algorithmen bezeichnen wir den einen Linienpunkt als $ X_ {0}, Y_ {0} $ und den zweiten Linienpunkt als $ X_ {1}, Y_ {1} $.

DDA-Algorithmus

Der Digital Differential Analyzer (DDA) -Algorithmus ist der einfache Zeilengenerierungsalgorithmus, der hier Schritt für Schritt erläutert wird.

Step 1 - Geben Sie die Eingabe von zwei Endpunkten $ (X_ {0}, Y_ {0}) $ und $ (X_ {1}, Y_ {1}) $ ein.

Step 2 - Berechnen Sie die Differenz zwischen zwei Endpunkten.

dx = X₁ - X₀
dy = Y₁ - Y₀

Step 3- Basierend auf der berechneten Differenz in Schritt 2 müssen Sie die Anzahl der Schritte zum Einfügen von Pixeln ermitteln. Wenn dx> dy, benötigen Sie weitere Schritte in der x-Koordinate. sonst in y-Koordinate.

if (absolute(dx) > absolute(dy))
   Steps = absolute(dx);
else
   Steps = absolute(dy);

Step 4 - Berechnen Sie das Inkrement in x-Koordinate und y-Koordinate.

Xincrement = dx / (float) steps;
Yincrement = dy / (float) steps;

Step 5 - Setzen Sie das Pixel, indem Sie die x- und y-Koordinaten erfolgreich entsprechend erhöhen, und vervollständigen Sie das Zeichnen der Linie.

for(int v=0; v < Steps; v++)
{
   x = x + Xincrement;
   y = y + Yincrement;
   putpixel(Round(x), Round(y));
}

Bresenhams Liniengenerierung

Der Bresenham-Algorithmus ist ein weiterer inkrementeller Scan-Konvertierungsalgorithmus. Der große Vorteil dieses Algorithmus besteht darin, dass nur ganzzahlige Berechnungen verwendet werden. Bewegen Sie sich in Einheitsintervallen über die x-Achse und wählen Sie bei jedem Schritt zwischen zwei verschiedenen y-Koordinaten.

Wie in der folgenden Abbildung gezeigt, müssen Sie beispielsweise an Position (2, 3) zwischen (3, 3) und (3, 4) wählen. Sie möchten den Punkt, der näher an der ursprünglichen Linie liegt.

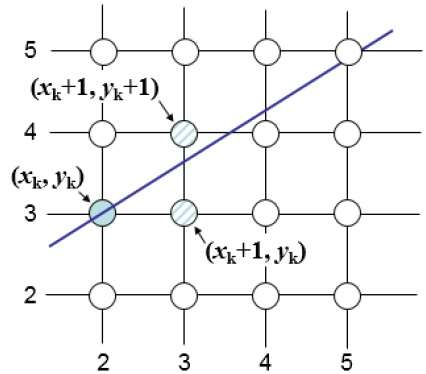
An der Probenposition $ X_ {k} + 1 werden $ die vertikalen Abstände von der mathematischen Linie als $ d_ {obere} $ und $ d_ {untere} $ bezeichnet.

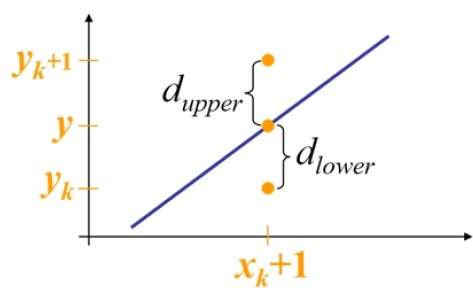
Aus der obigen Abbildung ist die y-Koordinate auf der mathematischen Linie bei $ x_ {k} + 1 $ -

Y = m ($ X_ {k} $ + 1) + b

Also werden $ d_ {obere} $ und $ d_ {untere} $ wie folgt angegeben:

$$ d_ {lower} = y-y_ {k} $$

$$ = m (X_ {k} + 1) + b - Y_ {k} $$

und

$$ d_ {obere} = (y_ {k} + 1) - y $$

$ = Y_ {k} + 1 - m (X_ {k} + 1) - b $

Mit diesen können Sie einfach entscheiden, welches Pixel näher an der mathematischen Linie liegt. Diese einfache Entscheidung basiert auf der Differenz zwischen den beiden Pixelpositionen.

$$ d_ {untere} - d_ {obere} = 2 m (x_ {k} + 1) - 2y_ {k} + 2b - 1 $$

Ersetzen wir m durch dy / dx, wobei dx und dy die Unterschiede zwischen den Endpunkten sind.

$$ dx (d_ {untere} - d_ {obere}) = dx (2 \ frac {\ mathrm {d} y} {\ mathrm {d} x} (x_ {k} + 1) - 2y_ {k} + 2b - 1) $$

$$ = 2dy.x_ {k} - 2dx.y_ {k} + 2dy + 2dx (2b-1) $$

$$ = 2dy.x_ {k} - 2dx.y_ {k} + C $$

Ein Entscheidungsparameter $ P_ {k} $ für den k- ten Schritt entlang einer Linie ist also gegeben durch -

$$ p_ {k} = dx (d_ {untere} - d_ {obere}) $$

$$ = 2dy.x_ {k} - 2dx.y_ {k} + C $$

Das Vorzeichen des Entscheidungsparameters $ P_ {k} $ ist das gleiche wie das von $ d_ {lower} - d_ {superior} $.

Wenn $ p_ {k} $ negativ ist, wählen Sie das untere Pixel, andernfalls das obere Pixel.

Denken Sie daran, dass die Koordinatenänderungen entlang der x-Achse in Einheitsschritten erfolgen, sodass Sie alles mit ganzzahligen Berechnungen ausführen können. In Schritt k + 1 wird der Entscheidungsparameter als - angegeben

$$ p_ {k +1} = 2dy.x_ {k + 1} - 2dx.y_ {k + 1} + C $$

Wenn wir $ p_ {k} $ davon abziehen, erhalten wir -

$$ p_ {k + 1} - p_ {k} = 2dy (x_ {k + 1} - x_ {k}) - 2dx (y_ {k + 1} - y_ {k}) $$

Aber $ x_ {k + 1} $ ist dasselbe wie $ (xk) + 1 $. Also -

$$ p_ {k + 1} = p_ {k} + 2dy - 2dx (y_ {k + 1} - y_ {k}) $$

Wobei $ Y_ {k + 1} - Y_ {k} $ je nach Vorzeichen von $ P_ {k} $ entweder 0 oder 1 ist.

Der erste Entscheidungsparameter $ p_ {0} $ wird ausgewertet mit $ (x_ {0}, y_ {0}) $ wird als - angegeben

$$ p_ {0} = 2dy - dx $$

Unter Berücksichtigung aller oben genannten Punkte und Berechnungen ist hier der Bresenham-Algorithmus für die Steigung m <1 -

Step 1 - Geben Sie die beiden Endpunkte der Linie ein und speichern Sie den linken Endpunkt in $ (x_ {0}, y_ {0}) $.

Step 2 - Zeichnen Sie den Punkt $ (x_ {0}, y_ {0}) $.

Step 3 - Berechnen Sie die Konstanten dx, dy, 2dy und (2dy - 2dx) und erhalten Sie den ersten Wert für den Entscheidungsparameter als -

$$ p_ {0} = 2dy - dx $$

Step 4 - Führen Sie an jedem $ X_ {k} $ entlang der Linie, beginnend bei k = 0, den folgenden Test durch:

Wenn $ p_ {k} $ <0 ist, ist der nächste zu zeichnende Punkt $ (x_ {k} +1, y_ {k}) $ und

$$ p_ {k + 1} = p_ {k} + 2dy $$ Andernfalls

$$ (x_ {k}, y_ {k} +1) $$

$$ p_ {k + 1} = p_ {k} + 2dy - 2dx $$

Step 5 - Wiederholen Sie Schritt 4 (dx - 1) Mal.

Finden Sie für m> 1 heraus, ob Sie x erhöhen müssen, während Sie y jedes Mal erhöhen.

Nach dem Lösen ist die Gleichung für den Entscheidungsparameter $ P_ {k} $ sehr ähnlich, nur das x und y in der Gleichung werden vertauscht.

Mittelpunkt-Algorithmus

Der Mittelpunktsalgorithmus geht auf Bresenham zurück, das von Pitteway und Van Aken modifiziert wurde. Angenommen, Sie haben den Punkt P bereits auf die (x, y) -Koordinate gesetzt und die Steigung der Linie ist 0 ≤ k ≤ 1, wie in der folgenden Abbildung gezeigt.

Nun müssen Sie entscheiden, ob der nächste Punkt bei E oder N platziert werden soll. Dies kann durch Identifizieren des Schnittpunkts Q gewählt werden, der dem Punkt N oder E am nächsten liegt. Wenn der Schnittpunkt Q dem Punkt N am nächsten liegt, wird N als betrachtet der nächste Punkt; sonst E.

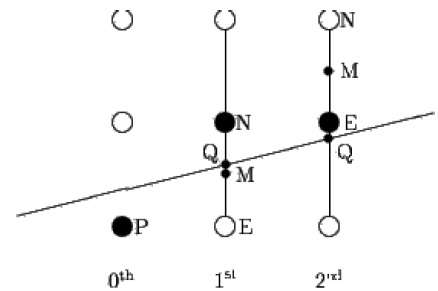
Um dies festzustellen, berechnen Sie zuerst den Mittelpunkt M (x + 1, y + ½). Wenn der Schnittpunkt Q der Linie mit der vertikalen Linie zwischen E und N unter M liegt, nehmen Sie E als nächsten Punkt. Andernfalls nehmen Sie N als nächsten Punkt.

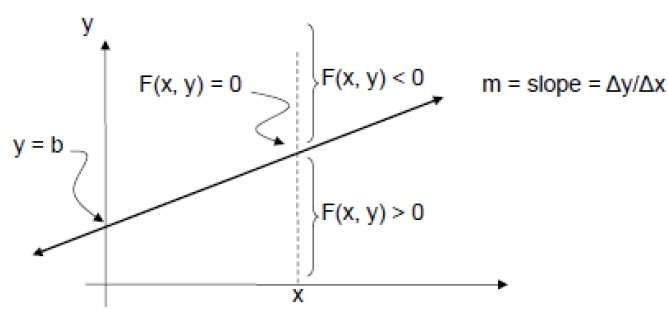
Um dies zu überprüfen, müssen wir die implizite Gleichung berücksichtigen -

F (x, y) = mx + b - y

Für positives m bei jedem gegebenen X,

Wenn y in der Zeile steht, ist F (x, y) = 0
Wenn y über der Linie liegt, ist F (x, y) <0
Wenn y unter der Linie liegt, ist F (x, y)> 0