Computergrafikkurven

In der Computergrafik müssen wir oft verschiedene Arten von Objekten auf den Bildschirm zeichnen. Objekte sind nicht immer flach und wir müssen viele Male Kurven zeichnen, um ein Objekt zu zeichnen.

Arten von Kurven

Eine Kurve ist eine unendlich große Menge von Punkten. Jeder Punkt hat zwei Nachbarn außer Endpunkten. Kurven können grob in drei Kategorien eingeteilt werden -explicit, implicit, und parametric curves.

Implizite Kurven

Implizite Kurvendarstellungen definieren die Menge der Punkte auf einer Kurve, indem ein Verfahren angewendet wird, mit dem geprüft werden kann, ob ein Punkt auf der Kurve liegt. Normalerweise wird eine implizite Kurve durch eine implizite Funktion der Form definiert -

f (x, y) = 0

Es kann mehrwertige Kurven darstellen (mehrere y-Werte für einen x-Wert). Ein häufiges Beispiel ist der Kreis, dessen implizite Darstellung ist

x² + y² - R² = 0

Explizite Kurven

Eine mathematische Funktion y = f (x) kann als Kurve aufgetragen werden. Eine solche Funktion ist die explizite Darstellung der Kurve. Die explizite Darstellung ist nicht allgemein, da sie keine vertikalen Linien darstellen kann und auch einwertig ist. Für jeden Wert von x wird normalerweise nur ein einziger Wert von y von der Funktion berechnet.

Parametrische Kurven

Kurven mit parametrischer Form werden als parametrische Kurven bezeichnet. Die expliziten und impliziten Kurvendarstellungen können nur verwendet werden, wenn die Funktion bekannt ist. In der Praxis werden die Parameterkurven verwendet. Eine zweidimensionale Parameterkurve hat die folgende Form:

P (t) = f (t), g (t) oder P (t) = x (t), y (t)

Die Funktionen f und g werden zu den (x, y) -Koordinaten eines beliebigen Punktes auf der Kurve, und die Punkte werden erhalten, wenn der Parameter t über ein bestimmtes Intervall [a, b] variiert wird, normalerweise [0, 1].

Bezierkurven

Die Bezier-Kurve wird vom französischen Ingenieur entdeckt Pierre Bézier. Diese Kurven können unter der Kontrolle anderer Punkte erzeugt werden. Ungefähre Tangenten unter Verwendung von Kontrollpunkten werden verwendet, um eine Kurve zu erzeugen. Die Bezier-Kurve kann mathematisch dargestellt werden als -

$$ \ sum_ {k = 0} ^ {n} P_ {i} {B_ {i} ^ {n}} (t) $$

Wobei $ p_ {i} $ die Menge der Punkte ist und $ {B_ {i} ^ {n}} (t) $ die Bernstein-Polynome darstellt, die durch - gegeben sind

$$ {B_ {i} ^ {n}} (t) = \ binom {n} {i} (1 - t) ^ {ni} t ^ {i} $$

Wo n ist der Polynomgrad, i ist der Index und t ist die Variable.

Die einfachste Bézier-Kurve ist die gerade Linie vom Punkt $ P_ {0} $ bis $ P_ {1} $. Eine quadratische Bezier-Kurve wird durch drei Kontrollpunkte bestimmt. Eine kubische Bezier-Kurve wird durch vier Kontrollpunkte bestimmt.

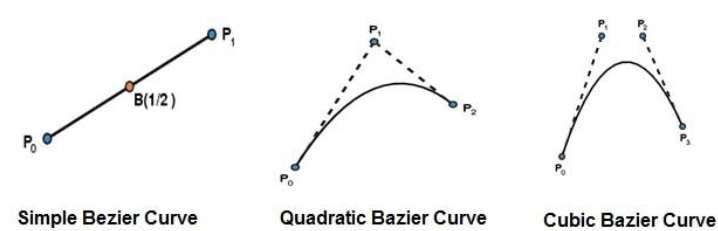
Eigenschaften von Bezierkurven

Bezierkurven haben folgende Eigenschaften:

Sie folgen im Allgemeinen der Form des Steuerpolygons, das aus den Segmenten besteht, die die Steuerpunkte verbinden.
Sie passieren immer den ersten und den letzten Kontrollpunkt.
Sie sind in der konvexen Hülle ihrer definierenden Kontrollpunkte enthalten.
Der Grad des Polynoms, das das Kurvensegment definiert, ist eins weniger als die Anzahl der definierenden Polygonpunkte. Daher beträgt für 4 Kontrollpunkte der Grad des Polynoms 3, dh das kubische Polynom.
Eine Bezier-Kurve folgt im Allgemeinen der Form des definierenden Polygons.
Die Richtung des Tangentenvektors an den Endpunkten ist dieselbe wie die des Vektors, der durch das erste und das letzte Segment bestimmt wird.
Die konvexe Hülleneigenschaft für eine Bezier-Kurve stellt sicher, dass das Polynom den Kontrollpunkten reibungslos folgt.
Keine gerade Linie schneidet eine Bezier-Kurve öfter als ihr Steuerpolygon.
Sie sind unter einer affinen Transformation unveränderlich.
Bezier-Kurven weisen globale Steuerungsmittel auf. Durch Bewegen eines Kontrollpunkts wird die Form der gesamten Kurve geändert.
Eine gegebene Bezier-Kurve kann an einem Punkt t = t0 in zwei Bezier-Segmente unterteilt werden, die sich an dem Punkt verbinden, der dem Parameterwert t = t0 entspricht.

B-Spline-Kurven

Die von der Bernstein-Basisfunktion erzeugte Bezier-Kurve weist eine begrenzte Flexibilität auf.

Erstens legt die Anzahl der angegebenen Polygonscheitelpunkte die Reihenfolge des resultierenden Polynoms fest, das die Kurve definiert.
Das zweite begrenzende Merkmal ist, dass der Wert der Mischfunktion für alle Parameterwerte über die gesamte Kurve ungleich Null ist.

Die B-Spline-Basis enthält als Sonderfall die Bernstein-Basis. Die B-Spline-Basis ist nicht global.

Eine B-Spline-Kurve ist definiert als eine lineare Kombination der Kontrollpunkte Pi und der B-Spline-Basisfunktion $ N_ {i,} $ k (t) gegeben durch

$ C (t) = \ sum_ {i = 0} ^ {n} P_ {i} N_ {i, k} (t), $ $ n \ geq k-1, $ $ t \: \ epsilon \: [ tk-1, tn + 1] $

Wo,

{$ p_ {i} $: i = 0, 1, 2… .n} sind die Kontrollpunkte
k ist die Reihenfolge der Polynomsegmente der B-Spline-Kurve. Ordnung k bedeutet, dass die Kurve aus stückweisen Polynomsegmenten vom Grad k - 1 besteht.
Die $ N_ {i, k} (t) $ sind die "normalisierten B-Spline-Mischfunktionen". Sie werden durch die Ordnung k und durch eine nicht abnehmende Folge von reellen Zahlen beschrieben, die normalerweise als "Knotenfolge" bezeichnet wird.

$$ {t_ {i}: i = 0, ... n + K} $$

Die N _i , k Funktionen werden wie folgt beschrieben:

$$ N_ {i, 1} (t) = \ left \ {\ begin {matrix} 1, & if \: u \: \ epsilon \: [t_ {i,} t_ {i + 1}) \\ 0 , & Andernfalls \ end {matrix} \ right. $$

und wenn k> 1 ist,

$$ N_ {i, k} (t) = \ frac {t-t_ {i}} {t_ {i + k-1}} N_ {i, k-1} (t) + \ frac {t_ {i + k} -t} {t_ {i + k} - t_ {i + 1}} N_ {i + 1, k-1} (t) $$

und

$$ t \: \ epsilon \: [t_ {k-1}, t_ {n + 1}) $$

Eigenschaften der B-Spline-Kurve

B-Spline-Kurven haben die folgenden Eigenschaften:

Die Summe der B-Spline-Basisfunktionen für jeden Parameterwert ist 1.
Jede Basisfunktion ist für alle Parameterwerte positiv oder Null.
Jede Basisfunktion hat bis auf k = 1 genau einen Maximalwert.
Die maximale Reihenfolge der Kurve entspricht der Anzahl der Eckpunkte des definierenden Polygons.
Der Grad des B-Spline-Polynoms ist unabhängig von der Anzahl der Eckpunkte des definierenden Polygons.
B-Spline ermöglicht die lokale Steuerung der Kurvenoberfläche, da jeder Scheitelpunkt die Form einer Kurve nur über einen Bereich von Parameterwerten beeinflusst, bei denen die zugehörige Basisfunktion ungleich Null ist.
Die Kurve zeigt die Variation verringernde Eigenschaft.
Die Kurve folgt im Allgemeinen der Form des definierenden Polygons.
Jede affine Transformation kann auf die Kurve angewendet werden, indem sie auf die Eckpunkte des definierenden Polygons angewendet wird.
Die Kurvenlinie innerhalb der konvexen Hülle des definierenden Polygons.