Algorithmus zur Kreiserzeugung

Das Zeichnen eines Kreises auf dem Bildschirm ist etwas komplexer als das Zeichnen einer Linie. Es gibt zwei beliebte Algorithmen zum Erzeugen eines Kreises -Bresenham’s Algorithm und Midpoint Circle Algorithm. Diese Algorithmen basieren auf der Idee, die nachfolgenden Punkte zu bestimmen, die zum Zeichnen des Kreises erforderlich sind. Lassen Sie uns die Algorithmen im Detail diskutieren -

Die Kreisgleichung lautet $ X ^ {2} + Y ^ {2} = r ^ {2}, $ wobei r der Radius ist.

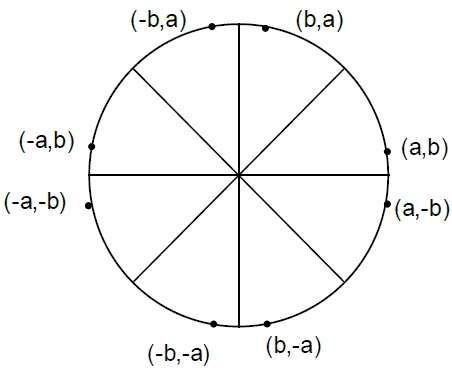
Bresenhams Algorithmus

Wir können keinen kontinuierlichen Bogen auf der Rasteranzeige anzeigen. Stattdessen müssen wir die nächste Pixelposition auswählen, um den Bogen zu vervollständigen.

Aus der folgenden Abbildung können Sie ersehen, dass wir das Pixel an der Position (X, Y) platziert haben und nun entscheiden müssen, wo das nächste Pixel platziert werden soll - bei N (X + 1, Y) oder bei S (X + 1, Y-1).

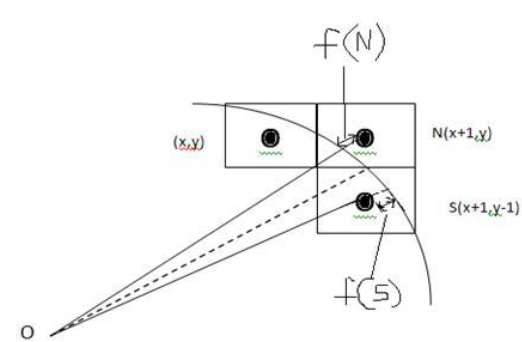
Dies kann durch den Entscheidungsparameter entschieden werden d.

Wenn d <= 0 ist, ist N (X + 1, Y) als nächstes Pixel zu wählen.
Wenn d> 0 ist, ist S (X + 1, Y-1) als nächstes Pixel zu wählen.

Algorithmus

Step 1- Ermitteln Sie die Koordinaten des Mittelpunkts des Kreises und des Radius und speichern Sie sie in x, y bzw. R. Setze P = 0 und Q = R.

Step 2 - Entscheidungsparameter D = 3 - 2R einstellen.

Step 3 - Wiederholen Sie Schritt 8, während P ≤ Q ist.

Step 4 - Zeichnen Sie Kreis zeichnen (X, Y, P, Q).

Step 5 - Erhöhen Sie den Wert von P.

Step 6 - Wenn D <0, dann ist D = D + 4P + 6.

Step 7 - Andernfalls setzen Sie R = R - 1, D = D + 4 (PQ) + 10.

Step 8 - Zeichnen Sie Kreis zeichnen (X, Y, P, Q).

Draw Circle Method(X, Y, P, Q).

Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).

Mittelpunkt-Algorithmus

Step 1 - Eingaberadius r und Kreismittelpunkt $ (x_ {c,} y_ {c}) $ und erhalten den ersten Punkt auf dem Umfang des Kreises, der auf dem Ursprung zentriert ist als

(x₀, y₀) = (0, r)

Step 2 - Berechnen Sie den Anfangswert des Entscheidungsparameters als

$ P_ {0} $ = 5/4 - r (Zur Vereinfachung dieser Gleichung siehe die folgende Beschreibung.)

f(x, y) = x² + y² - r² = 0

f(x_i - 1/2 + e, y_i + 1)
        = (x_i - 1/2 + e)² + (y_i + 1)² - r² 
        = (x_i- 1/2)² + (y_i + 1)² - r² + 2(x_i - 1/2)e + e²
        = f(x_i - 1/2, y_i + 1) + 2(x_i - 1/2)e + e² = 0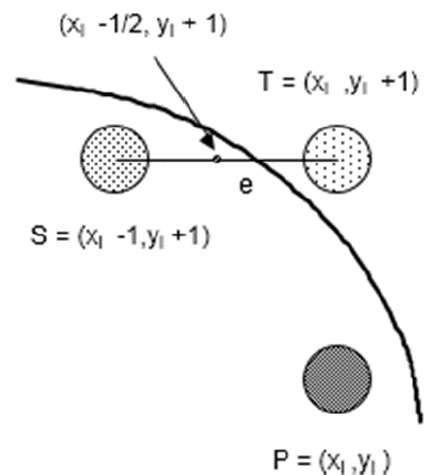

Let d_i = f(x_i - 1/2, y_i + 1) = -2(x_i - 1/2)e - e²
Thus,

If e < 0 then di > 0 so choose point S = (x_i - 1, y_i + 1).
d_i+1    = f(x_i - 1 - 1/2, y_i + 1 + 1) = ((x_i - 1/2) - 1)² + ((y_i + 1) + 1)² - r²
        = d_i - 2(x_i - 1) + 2(y_i + 1) + 1
        = d_i + 2(y_{i + 1} - x_{i + 1}) + 1
		  
If e >= 0 then di <= 0 so choose point T = (x_i, y_i + 1)
   d_i+1 = f(x_i - 1/2, y_i + 1 + 1)
       = d_i + 2y_i+1 + 1
		  
The initial value of di is
   d₀ = f(r - 1/2, 0 + 1) = (r - 1/2)² + 1² - r²
      = 5/4 - r {1-r can be used if r is an integer}
		
When point S = (x_i - 1, y_i + 1) is chosen then
   d_i+1 = d_i + -2x_i+1 + 2y_i+1 + 1
	
When point T = (x_i, y_i + 1) is chosen then
   d_i+1 = d_i + 2y_i+1 + 1

Step 3 - Führen Sie an jeder Position $ X_ {K} $ ab K = 0 den folgenden Test durch:

If P_K < 0 then next point on circle (0,0) is (X_K+1,Y_K) and
   P_K+1 = P_K + 2X_K+1 + 1
Else
   P_K+1 = P_K + 2X_K+1 + 1 – 2Y_K+1
	
Where, 2X_K+1 = 2X_K+2 and 2Y_K+1 = 2Y_K-2.

Step 4 - Bestimmen Sie die Symmetriepunkte in anderen sieben Oktanten.

Step 5 - Verschieben Sie jede berechnete Pixelposition (X, Y) auf die auf $ (X_ {C,} Y_ {C}) $ zentrierte Kreisbahn und zeichnen Sie die Koordinatenwerte auf.

X = X + X_C,   Y = Y + Y_C

Step 6 - Wiederholen Sie die Schritte 3 bis 5, bis X> = Y.