TensorFlow - Conceptos básicos
En este capítulo, aprenderemos los conceptos básicos de TensorFlow. Comenzaremos por comprender la estructura de datos del tensor.
Estructura de datos del tensor
Los tensores se utilizan como estructuras de datos básicas en el lenguaje TensorFlow. Los tensores representan los bordes de conexión en cualquier diagrama de flujo llamado Gráfico de flujo de datos. Los tensores se definen como matriz o lista multidimensional.
Los tensores se identifican mediante los siguientes tres parámetros:
Rango
La unidad de dimensionalidad descrita dentro del tensor se llama rango. Identifica el número de dimensiones del tensor. Un rango de un tensor puede describirse como el orden o las n dimensiones de un tensor definido.
Forma
El número de filas y columnas juntas define la forma de Tensor.
Tipo
Type describe el tipo de datos asignado a los elementos de Tensor.
Un usuario debe considerar las siguientes actividades para construir un tensor:
- Construye una matriz n-dimensional
- Convierta la matriz n-dimensional.
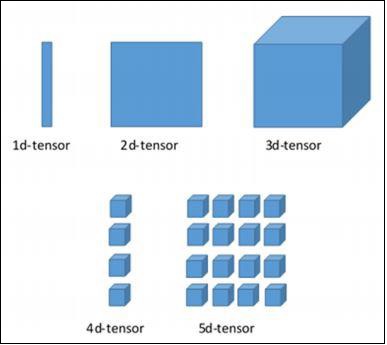
Varias dimensiones de TensorFlow
TensorFlow incluye varias dimensiones. Las dimensiones se describen brevemente a continuación:
Tensor unidimensional
El tensor unidimensional es una estructura de matriz normal que incluye un conjunto de valores del mismo tipo de datos.
Declaration
>>> import numpy as np
>>> tensor_1d = np.array([1.3, 1, 4.0, 23.99])
>>> print tensor_1dLa implementación con la salida se muestra en la captura de pantalla a continuación:
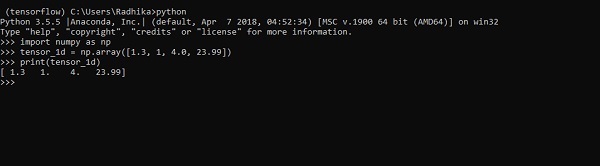
La indexación de elementos es la misma que la de las listas de Python. El primer elemento comienza con un índice de 0; para imprimir los valores a través del índice, todo lo que necesita hacer es mencionar el número de índice.
>>> print tensor_1d[0]
1.3
>>> print tensor_1d[2]
4.0
Tensores bidimensionales
La secuencia de matrices se utiliza para crear "tensores bidimensionales".
La creación de tensores bidimensionales se describe a continuación:

A continuación se muestra la sintaxis completa para crear matrices bidimensionales:
>>> import numpy as np
>>> tensor_2d = np.array([(1,2,3,4),(4,5,6,7),(8,9,10,11),(12,13,14,15)])
>>> print(tensor_2d)
[[ 1 2 3 4]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]]
>>>Los elementos específicos de los tensores bidimensionales se pueden rastrear con la ayuda del número de fila y el número de columna especificados como números de índice.
>>> tensor_2d[3][2]
14
Manejo y manipulaciones de tensores
En esta sección, aprenderemos sobre el manejo y las manipulaciones de tensores.
Para empezar, consideremos el siguiente código:
import tensorflow as tf
import numpy as np
matrix1 = np.array([(2,2,2),(2,2,2),(2,2,2)],dtype = 'int32')
matrix2 = np.array([(1,1,1),(1,1,1),(1,1,1)],dtype = 'int32')
print (matrix1)
print (matrix2)
matrix1 = tf.constant(matrix1)
matrix2 = tf.constant(matrix2)
matrix_product = tf.matmul(matrix1, matrix2)
matrix_sum = tf.add(matrix1,matrix2)
matrix_3 = np.array([(2,7,2),(1,4,2),(9,0,2)],dtype = 'float32')
print (matrix_3)
matrix_det = tf.matrix_determinant(matrix_3)
with tf.Session() as sess:
result1 = sess.run(matrix_product)
result2 = sess.run(matrix_sum)
result3 = sess.run(matrix_det)
print (result1)
print (result2)
print (result3)Output
El código anterior generará la siguiente salida:
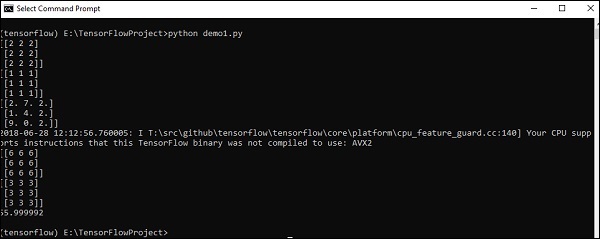
Explicación
Hemos creado matrices multidimensionales en el código fuente anterior. Ahora, es importante entender que creamos gráficos y sesiones, que administran los tensores y generan la salida adecuada. Con la ayuda del gráfico, tenemos la salida que especifica los cálculos matemáticos entre tensores.