TensorFlow - Fundamentos matemáticos
Es importante comprender los conceptos matemáticos necesarios para TensorFlow antes de crear la aplicación básica en TensorFlow. Las matemáticas se consideran el corazón de cualquier algoritmo de aprendizaje automático. Es con la ayuda de los conceptos básicos de las matemáticas, se define una solución para un algoritmo específico de aprendizaje automático.
Vector
Una matriz de números, que es continua o discreta, se define como un vector. Los algoritmos de aprendizaje automático se ocupan de vectores de longitud fija para una mejor generación de resultados.
Los algoritmos de aprendizaje automático manejan datos multidimensionales, por lo que los vectores juegan un papel crucial.

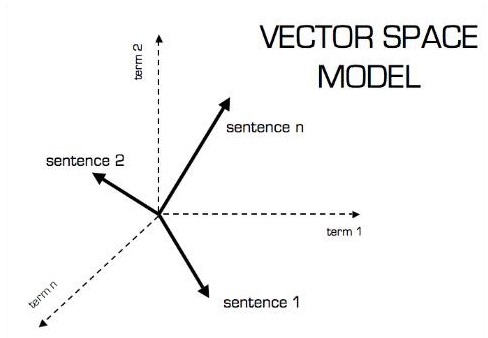
La representación pictórica del modelo vectorial es la que se muestra a continuación:
Escalar
El escalar se puede definir como un vector unidimensional. Los escalares son aquellos que incluyen solo magnitud y ninguna dirección. Con los escalares, solo nos preocupa la magnitud.
Los ejemplos de escalar incluyen parámetros de peso y altura de los niños.
Matriz
Matrix se puede definir como matrices multidimensionales, que se organizan en formato de filas y columnas. El tamaño de la matriz se define por la longitud de la fila y la longitud de la columna. La siguiente figura muestra la representación de cualquier matriz especificada.
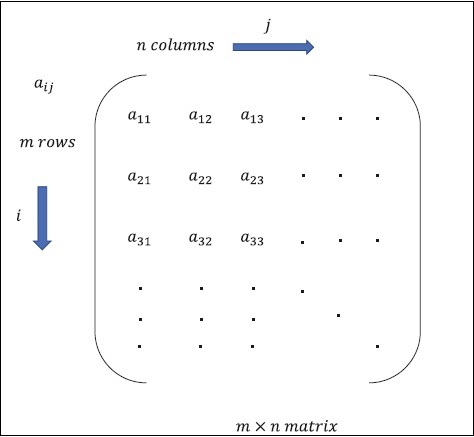
Considere la matriz con "m" filas y "n" columnas como se mencionó anteriormente, la representación de la matriz se especificará como "m * n matriz" que definió la longitud de la matriz también.
Cálculos matemáticos
En esta sección, aprenderemos sobre los diferentes cálculos matemáticos en TensorFlow.
Adición de matrices
La adición de dos o más matrices es posible si las matrices son de la misma dimensión. La adición implica la adición de cada elemento según la posición dada.
Considere el siguiente ejemplo para comprender cómo funciona la suma de matrices:
$$ Ejemplo: A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B = \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} \: luego \: A + B = \ begin {bmatrix} 1 + 5 & 2 + 6 \\ 3 + 7 & 4 + 8 \ end {bmatrix} = \ begin {bmatrix} 6 & 8 \\ 10 & 12 \ end {bmatrix} $$
Resta de matrices
La resta de matrices opera de manera similar a la suma de dos matrices. El usuario puede restar dos matrices siempre que las dimensiones sean iguales.
$$ Ejemplo: A- \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B- \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} \: luego \: AB - \ begin {bmatrix} 1-5 y 2-6 \\ 3-7 y 4-8 \ end {bmatrix} - \ begin {bmatrix} -4 y -4 \\ - 4 y -4 \ end {bmatrix} $$
Multiplicación de matrices
Para que dos matrices A m * n y B p * q sean multiplicables, n debe ser igual a p. La matriz resultante es -
C m * q
$$ A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} B = \ begin {bmatrix} 5 & 6 \\ 7 & 8 \ end {bmatrix} $$
$$ c_ {11} = \ begin {bmatrix} 1 & 2 \ end {bmatrix} \ begin {bmatrix} 5 \\ 7 \ end {bmatrix} = 1 \ times5 + 2 \ times7 = 19 \: c_ {12} = \ begin {bmatrix} 1 & 2 \ end {bmatrix} \ begin {bmatrix} 6 \\ 8 \ end {bmatrix} = 1 \ times6 + 2 \ times8 = 22 $$
$$ c_ {21} = \ begin {bmatrix} 3 & 4 \ end {bmatrix} \ begin {bmatrix} 5 \\ 7 \ end {bmatrix} = 3 \ times5 + 4 \ times7 = 43 \: c_ {22} = \ begin {bmatrix} 3 & 4 \ end {bmatrix} \ begin {bmatrix} 6 \\ 8 \ end {bmatrix} = 3 \ times6 + 4 \ times8 = 50 $$
$$ C = \ begin {bmatrix} c_ {11} & c_ {12} \\ c_ {21} & c_ {22} \ end {bmatrix} = \ begin {bmatrix} 19 & 22 \\ 43 & 50 \ end {bmatrix} $$
Transponer de matriz
La transposición de una matriz A, m * n generalmente se representa mediante AT (transposición) n * my se obtiene transponiendo los vectores de columna como vectores de fila.
$$ Ejemplo: A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} \: luego \: A ^ {T} \ begin {bmatrix} 1 & 3 \\ 2 & 4 \ end { bmatrix} $$
Producto escalar de vectores
Cualquier vector de dimensión n puede representarse como una matriz v = R ^ n * 1.
$$ v_ {1} = \ begin {bmatrix} v_ {11} \\ v_ {12} \\\ cdot \\\ cdot \\\ cdot \\ v_ {1n} \ end {bmatrix} v_ {2} = \ begin {bmatrix} v_ {21} \\ v_ {22} \\\ cdot \\\ cdot \\\ cdot \\ v_ {2n} \ end {bmatrix} $$
El producto escalar de dos vectores es la suma del producto de los componentes correspondientes - Componentes a lo largo de la misma dimensión y se puede expresar como
$$ v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = v_2 ^ Tv_ {1} = v_ {11} v_ {21} + v_ {12} v_ {22} + \ cdot \ cdot + v_ {1n} v_ {2n} = \ Displaystyle \ sum \ limits_ {k = 1} ^ n v_ {1k} v_ {2k} $$
El ejemplo de producto escalar de vectores se menciona a continuación:
$$ Ejemplo: v_ {1} = \ begin {bmatrix} 1 \\ 2 \\ 3 \ end {bmatrix} v_ {2} = \ begin {bmatrix} 3 \\ 5 \\ - 1 \ end {bmatrix} v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = 1 \ times3 + 2 \ times5-3 \ times1 = 10 $$