TensorFlow: redes neuronales recurrentes
Las redes neuronales recurrentes son un tipo de algoritmo orientado al aprendizaje profundo, que sigue un enfoque secuencial. En las redes neuronales, siempre asumimos que cada entrada y salida es independiente de todas las demás capas. Este tipo de redes neuronales se denominan recurrentes porque realizan cálculos matemáticos de manera secuencial.
Considere los siguientes pasos para entrenar una red neuronal recurrente:
Step 1 - Ingrese un ejemplo específico del conjunto de datos.
Step 2 - Network tomará un ejemplo y calculará algunos cálculos utilizando variables inicializadas aleatoriamente.
Step 3 - A continuación, se calcula un resultado previsto.
Step 4 - La comparación del resultado real generado con el valor esperado producirá un error.
Step 5 - Para rastrear el error, se propaga por el mismo camino donde también se ajustan las variables.
Step 6 - Se repiten los pasos del 1 al 5 hasta que estemos seguros de que las variables declaradas para obtener la salida están definidas correctamente.
Step 7 - Se realiza una predicción sistemática aplicando estas variables para obtener nuevas entradas invisibles.
El enfoque esquemático de representar redes neuronales recurrentes se describe a continuación:
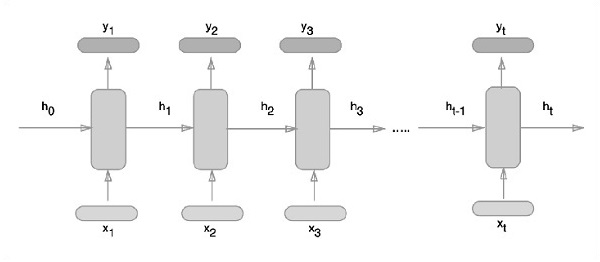
Implementación recurrente de redes neuronales con TensorFlow
En esta sección, aprenderemos cómo implementar una red neuronal recurrente con TensorFlow.
Step 1 - TensorFlow incluye varias bibliotecas para la implementación específica del módulo de red neuronal recurrente.
#Import necessary modules
from __future__ import print_function
import tensorflow as tf
from tensorflow.contrib import rnn
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)Como se mencionó anteriormente, las bibliotecas ayudan a definir los datos de entrada, que forman la parte principal de la implementación de la red neuronal recurrente.
Step 2- Nuestro motivo principal es clasificar las imágenes utilizando una red neuronal recurrente, donde consideramos cada fila de imágenes como una secuencia de píxeles. La forma de la imagen MNIST se define específicamente como 28 * 28 px. Ahora manejaremos 28 secuencias de 28 pasos para cada muestra que se menciona. Definiremos los parámetros de entrada para realizar el patrón secuencial.
n_input = 28 # MNIST data input with img shape 28*28
n_steps = 28
n_hidden = 128
n_classes = 10
# tf Graph input
x = tf.placeholder("float", [None, n_steps, n_input])
y = tf.placeholder("float", [None, n_classes]
weights = {
'out': tf.Variable(tf.random_normal([n_hidden, n_classes]))
}
biases = {
'out': tf.Variable(tf.random_normal([n_classes]))
}Step 3- Calcule los resultados utilizando una función definida en RNN para obtener los mejores resultados. Aquí, cada forma de datos se compara con la forma de entrada actual y los resultados se calculan para mantener la tasa de precisión.
def RNN(x, weights, biases):
x = tf.unstack(x, n_steps, 1)
# Define a lstm cell with tensorflow
lstm_cell = rnn.BasicLSTMCell(n_hidden, forget_bias=1.0)
# Get lstm cell output
outputs, states = rnn.static_rnn(lstm_cell, x, dtype = tf.float32)
# Linear activation, using rnn inner loop last output
return tf.matmul(outputs[-1], weights['out']) + biases['out']
pred = RNN(x, weights, biases)
# Define loss and optimizer
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = pred, labels = y))
optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cost)
# Evaluate model
correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
# Initializing the variables
init = tf.global_variables_initializer()Step 4- En este paso, lanzaremos el gráfico para obtener los resultados computacionales. Esto también ayuda a calcular la precisión de los resultados de las pruebas.
with tf.Session() as sess:
sess.run(init)
step = 1
# Keep training until reach max iterations
while step * batch_size < training_iters:
batch_x, batch_y = mnist.train.next_batch(batch_size)
batch_x = batch_x.reshape((batch_size, n_steps, n_input))
sess.run(optimizer, feed_dict={x: batch_x, y: batch_y})
if step % display_step == 0:
# Calculate batch accuracy
acc = sess.run(accuracy, feed_dict={x: batch_x, y: batch_y})
# Calculate batch loss
loss = sess.run(cost, feed_dict={x: batch_x, y: batch_y})
print("Iter " + str(step*batch_size) + ", Minibatch Loss= " + \
"{:.6f}".format(loss) + ", Training Accuracy= " + \
"{:.5f}".format(acc))
step += 1
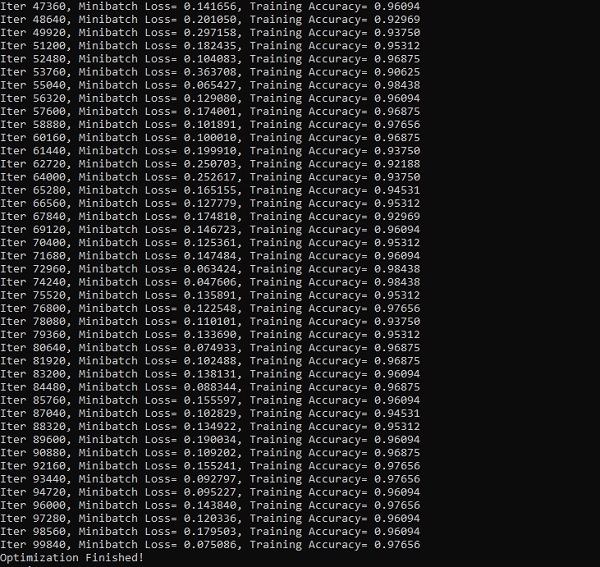
print("Optimization Finished!")
test_len = 128
test_data = mnist.test.images[:test_len].reshape((-1, n_steps, n_input))
test_label = mnist.test.labels[:test_len]
print("Testing Accuracy:", \
sess.run(accuracy, feed_dict={x: test_data, y: test_label}))Las capturas de pantalla a continuación muestran la salida generada: