TensorFlow: perceptrón de una sola capa

Para comprender el perceptrón de una sola capa, es importante comprender las redes neuronales artificiales (ANN). Las redes neuronales artificiales son el sistema de procesamiento de información cuyo mecanismo está inspirado en la funcionalidad de los circuitos neuronales biológicos. Una red neuronal artificial posee muchas unidades de procesamiento conectadas entre sí. A continuación se muestra la representación esquemática de la red neuronal artificial:

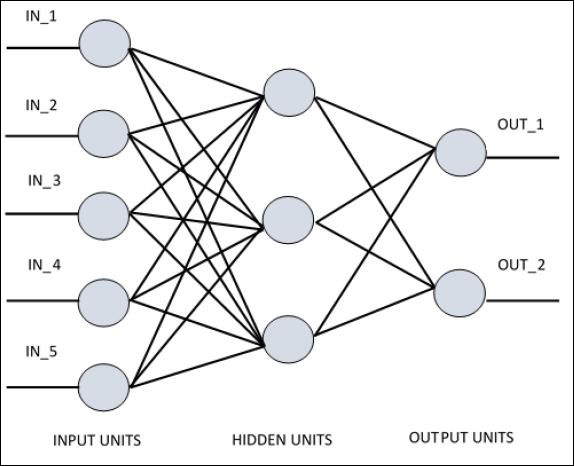
El diagrama muestra que las unidades ocultas se comunican con la capa externa. Mientras que las unidades de entrada y salida se comunican solo a través de la capa oculta de la red.

El patrón de conexión con los nodos, el número total de capas y el nivel de nodos entre entradas y salidas con el número de neuronas por capa definen la arquitectura de una red neuronal.

Hay dos tipos de arquitectura. Estos tipos se centran en la funcionalidad de las redes neuronales artificiales de la siguiente manera:

Perceptrón de una sola capa
Perceptrón multicapa

Perceptrón de una sola capa

El perceptrón de capa única es el primer modelo neuronal propuesto creado. El contenido de la memoria local de la neurona consiste en un vector de pesos. El cálculo de un perceptrón de capa única se realiza sobre el cálculo de la suma del vector de entrada, cada uno con el valor multiplicado por el elemento correspondiente del vector de los pesos. El valor que se muestra en la salida será la entrada de una función de activación.

Centrémonos en la implementación del perceptrón de una sola capa para un problema de clasificación de imágenes mediante TensorFlow. El mejor ejemplo para ilustrar el perceptrón de una sola capa es a través de la representación de "Regresión logística".

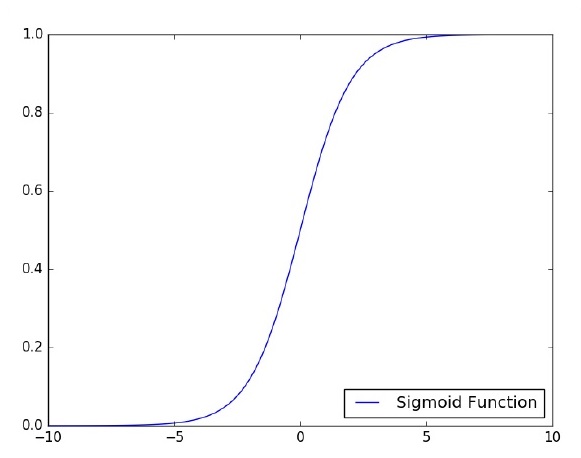
Ahora, consideremos los siguientes pasos básicos para entrenar la regresión logística:

Los pesos se inicializan con valores aleatorios al comienzo del entrenamiento.
Para cada elemento del conjunto de entrenamiento, el error se calcula con la diferencia entre la salida deseada y la salida real. El error calculado se utiliza para ajustar los pesos.
El proceso se repite hasta que el error cometido en todo el conjunto de entrenamiento no es menor que el umbral especificado, hasta que se alcanza el número máximo de iteraciones.

El código completo para la evaluación de la regresión logística se menciona a continuación:

# Import MINST data 
from tensorflow.examples.tutorials.mnist import input_data 
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True) 

import tensorflow as tf 
import matplotlib.pyplot as plt 

# Parameters 
learning_rate = 0.01 
training_epochs = 25 
batch_size = 100 
display_step = 1 

# tf Graph Input 
x = tf.placeholder("float", [None, 784]) # mnist data image of shape 28*28 = 784 
y = tf.placeholder("float", [None, 10]) # 0-9 digits recognition => 10 classes 

# Create model 
# Set model weights 
W = tf.Variable(tf.zeros([784, 10])) 
b = tf.Variable(tf.zeros([10])) 

# Construct model 
activation = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax 

# Minimize error using cross entropy 
cross_entropy = y*tf.log(activation) 
cost = tf.reduce_mean\ (-tf.reduce_sum\ (cross_entropy,reduction_indices = 1)) 

optimizer = tf.train.\ GradientDescentOptimizer(learning_rate).minimize(cost) 

#Plot settings 
avg_set = [] 
epoch_set = [] 

# Initializing the variables init = tf.initialize_all_variables()
# Launch the graph 
with tf.Session() as sess:
   sess.run(init)
   
   # Training cycle
   for epoch in range(training_epochs):
      avg_cost = 0.
      total_batch = int(mnist.train.num_examples/batch_size)
      
      # Loop over all batches
      for i in range(total_batch):
         batch_xs, batch_ys = \ mnist.train.next_batch(batch_size)
         # Fit training using batch data sess.run(optimizer, \ feed_dict = {
            x: batch_xs, y: batch_ys}) 
         # Compute average loss avg_cost += sess.run(cost, \ feed_dict = {
            x: batch_xs, \ y: batch_ys})/total_batch
      # Display logs per epoch step
      if epoch % display_step == 0:
         print ("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost))
            avg_set.append(avg_cost) epoch_set.append(epoch+1)
   print ("Training phase finished")
    
   plt.plot(epoch_set,avg_set, 'o', label = 'Logistic Regression Training phase') 
   plt.ylabel('cost') 
   plt.xlabel('epoch') 
   plt.legend() 
   plt.show() 
    
   # Test model 
   correct_prediction = tf.equal(tf.argmax(activation, 1), tf.argmax(y, 1)) 
   
   # Calculate accuracy 
   accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print 
      ("Model accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))

Salida

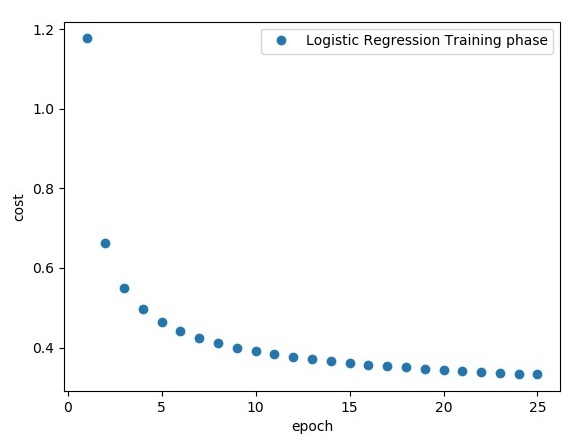
El código anterior genera la siguiente salida:

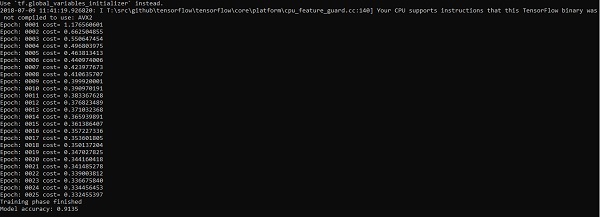
La regresión logística se considera un análisis predictivo. La regresión logística se utiliza para describir datos y explicar la relación entre una variable binaria dependiente y una o más variables nominales o independientes.