Concept de convolution

Ce didacticiel concerne l'un des concepts très importants de signaux et de système. Nous discuterons complètement de la convolution. Qu'Est-ce que c'est? Pourquoi ça? Que pouvons-nous faire avec?

Nous commencerons à discuter de la convolution à partir des bases du traitement d'image.

Qu'est-ce que le traitement d'image

Comme nous l'avons vu dans l'introduction aux tutoriels de traitement d'image et dans le signal et le système, ce traitement d'image est plus ou moins l'étude des signaux et des systèmes car une image n'est rien d'autre qu'un signal bidimensionnel.

Nous avons également discuté que dans le traitement d'image, nous développons un système dont l'entrée est une image et la sortie serait une image. Ceci est représenté sous forme d'image.

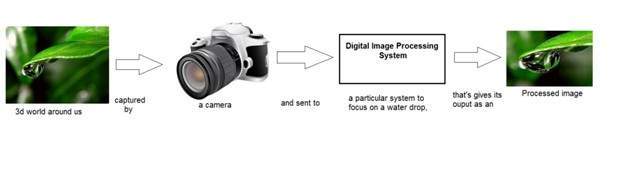
La boîte est celle illustrée dans la figure ci-dessus intitulée «Système de traitement d'image numérique» pourrait être considérée comme une boîte noire

Il peut être mieux représenté comme:

Où avons-nous atteint jusqu'à maintenant

Jusqu'à présent, nous avons discuté de deux méthodes importantes pour manipuler les images. Ou en d'autres termes, nous pouvons dire que notre boîte noire fonctionne de deux manières différentes jusqu'à présent.

Les deux manières différentes de manipuler les images étaient

Graphiques (histogrammes)

Cette méthode est connue sous le nom de traitement d'histogramme. Nous en avons discuté en détail dans les tutoriels précédents pour augmenter le contraste, l'amélioration de l'image, la luminosité, etc.

Fonctions de transformation

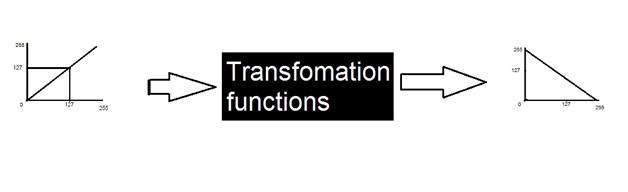
Cette méthode est connue sous le nom de transformations, dans laquelle nous avons discuté de différents types de transformations et de certaines transformations de niveaux de gris

Une autre façon de traiter les images

Ici, nous allons discuter d'une autre méthode de traitement des images. Cette autre méthode est connue sous le nom de convolution. Habituellement, la boîte noire (système) utilisée pour le traitement d'image est un système LTI ou un système invariant dans le temps linéaire. Par linéaire, nous entendons un tel système où la sortie est toujours linéaire, ni logarithmique ni exposant ou autre. Et par invariant dans le temps, nous entendons un système qui reste le même pendant le temps.

Alors maintenant, nous allons utiliser cette troisième méthode. Il peut être représenté par.

Il peut être représenté mathématiquement de deux manières

g(x,y) = h(x,y) * f(x,y)

Cela peut être expliqué comme le «masque convolué avec une image».

g(x,y) = f(x,y) * h(x,y)

Cela peut être expliqué par «image convoluée avec masque».

Il y a deux façons de représenter cela car l'opérateur de convolution (*) est commutatif. Le h (x, y) est le masque ou le filtre.

Qu'est-ce que le masque?

Le masque est également un signal. Il peut être représenté par une matrice bidimensionnelle. Le masque est généralement de l'ordre de 1x1, 3x3, 5x5, 7x7. Un masque doit toujours être en nombre impair, car sinon vous ne pouvez pas trouver le milieu du masque. Pourquoi avons-nous besoin de trouver le milieu du masque. La réponse se trouve ci-dessous, dans le sujet de, comment effectuer la convolution?

Comment effectuer la convolution?

Afin d'effectuer la convolution sur une image, les étapes suivantes doivent être prises.

Retourner le masque (horizontalement et verticalement) une seule fois
Faites glisser le masque sur l'image.
Multipliez les éléments correspondants puis ajoutez-les
Répétez cette procédure jusqu'à ce que toutes les valeurs de l'image aient été calculées.

Exemple de convolution

Faisons une convolution. L'étape 1 consiste à retourner le masque.

Masque

Prenons notre masque pour être ceci.

1	2	3
4	5	6
sept	8	9

Retourner le masque horizontalement

3	2	1
6	5	4
9	8	sept

Retourner le masque verticalement

9	8	sept
6	5	4
3	2	1

Image

Considérons une image comme ceci

2	4	6
8	dix	12
14	16	18

Convolution

Masque de convolution sur l'image. C'est fait de cette manière. Placez le centre du masque sur chaque élément d'une image. Multipliez les éléments correspondants puis ajoutez-les, et collez le résultat sur l'élément de l'image sur lequel vous placez le centre du masque.

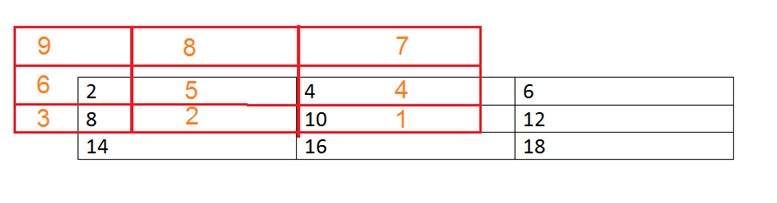
La boîte en rouge est le masque et les valeurs en orange sont les valeurs du masque. La zone de couleur noire et les valeurs appartiennent à l'image. Maintenant, pour le premier pixel de l'image, la valeur sera calculée comme

Premier pixel = (5 * 2) + (4 * 4) + (2 * 8) + (1 * 10)

= 10 + 16 + 16 + 10

= 52

Placez 52 dans l'image d'origine au premier index et répétez cette procédure pour chaque pixel de l'image.

Pourquoi la convolution

La convolution peut réaliser quelque chose que les deux méthodes précédentes de manipulation d'images ne peuvent pas réaliser. Ceux-ci incluent le flou, la netteté, la détection des contours, la réduction du bruit, etc.