Filtres passe-haut et passe-bas
Dans le dernier didacticiel, nous abordons brièvement les filtres. Dans ce didacticiel, nous en discuterons en détail. Avant de discuter de, parlons d'abord des masques. Le concept de masque a été abordé dans notre tutoriel sur la convolution et les masques.
Masques flous vs masques dérivés
Nous allons effectuer une comparaison entre les masques de flou et les masques dérivés.
Masques flous
Un masque de flou a les propriétés suivantes.
- Toutes les valeurs des masques de flou sont positives
- La somme de toutes les valeurs est égale à 1
- Le contenu des bords est réduit à l'aide d'un masque de flou
- Au fur et à mesure que la taille du masque grandit, un effet plus lissant se produira
Masques dérivés
Un masque dérivé a les propriétés suivantes.
- Un masque dérivé a des valeurs positives et négatives
- La somme de toutes les valeurs d'un masque dérivé est égale à zéro
- Le contenu des bords est augmenté par un masque dérivé
- À mesure que la taille du masque augmente, le contenu des bords augmente
Relation entre le masque de flou et le masque dérivé avec les filtres passe-haut et les filtres passe-bas.
La relation entre le masque de flou et le masque dérivé avec un filtre passe-haut et un filtre passe-bas peut être définie simplement comme.
- Les masques de flou sont également appelés filtre passe-bas
- Les masques dérivés sont également appelés filtre passe-haut
Composants de fréquence passe-haut et composants de fréquence passe-bas
Les composantes de fréquence passe-haut désignent les bords tandis que les composantes de fréquence passe-bas désignent des régions lisses.
Filtre passe-bas idéal et filtre passe-haut idéal
C'est l'exemple courant de filtre passe-bas.
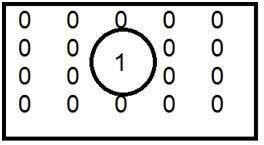
Quand on est placé à l'intérieur et que le zéro est placé à l'extérieur, nous avons une image floue. Maintenant que nous augmentons la taille de 1, le flou serait augmenté et le contenu des bords serait réduit.
Ceci est un exemple courant de filtre passe-haut.
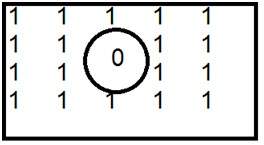
Lorsque 0 est placé à l'intérieur, nous obtenons des bords, ce qui nous donne une image esquissée. Un filtre passe-bas idéal dans le domaine fréquentiel est donné ci-dessous.

Le filtre passe-bas idéal peut être représenté graphiquement comme
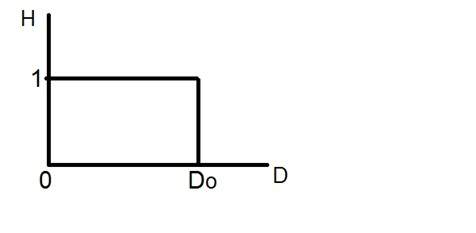
Maintenant, appliquons ce filtre à une image réelle et voyons ce que nous avons.
Exemple d'image

Image dans le domaine fréquentiel

Appliquer un filtre sur cette image

Image résultante

De la même manière, un filtre passe-haut idéal peut être appliqué sur une image. Mais évidemment, les résultats seraient différents car le passe-bas réduit le contenu tranchant et le passe-haut l'augmente.
Filtre passe-bas gaussien et passe-haut gaussien
Le filtre passe-bas gaussien et passe-haut gaussien minimise le problème qui se produit dans un filtre passe-bas et passe-haut idéal.
Ce problème est connu sous le nom d'effet de sonnerie. Cela est dû au fait qu'à certains points, la transition d'une couleur à l'autre ne peut pas être définie avec précision, en raison de laquelle l'effet de sonnerie apparaît à ce point.
Jetez un œil à ce graphique.
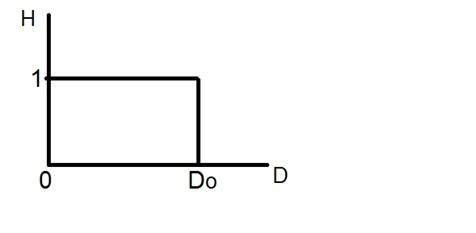
C'est la représentation du filtre passe-bas idéal. Maintenant, au point exact de Do, vous ne pouvez pas dire que la valeur serait 0 ou 1. En raison de laquelle l'effet de sonnerie apparaît à ce point.
Ainsi, afin de réduire l'effet qui apparaît comme un filtre passe-bas idéal et un filtre passe-haut idéal, le filtre passe-bas gaussien et le filtre passe-haut gaussien suivants sont introduits.
Filtre passe-bas gaussien
Le concept de filtrage et de passe-bas reste le même, mais seule la transition devient différente et devient plus douce.
Le filtre passe-bas gaussien peut être représenté par

Notez la transition de courbe douce, grâce à laquelle, à chaque point, la valeur de Do peut être définie avec précision.
Filtre passe-haut gaussien
Le filtre passe-haut gaussien a le même concept que le filtre passe-haut idéal, mais là encore, la transition est plus douce que celle idéale.