Théorème de convolution
Dans le dernier tutoriel, nous avons discuté des images dans le domaine fréquentiel. Dans ce tutoriel, nous allons définir une relation entre le domaine fréquentiel et les images (domaine spatial).
Par exemple
Prenons cet exemple.

La même image dans le domaine fréquentiel peut être représentée par.

Maintenant, quelle est la relation entre l'image ou le domaine spatial et le domaine de fréquence. Cette relation peut être expliquée par un théorème appelé théorème de convolution.
Théorème de convolution
La relation entre le domaine spatial et le domaine fréquentiel peut être établie par le théorème de convolution.
Le théorème de convolution peut être représenté par.
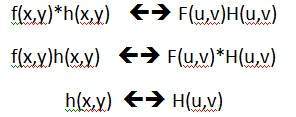
On peut dire que la convolution dans le domaine spatial est égale au filtrage dans le domaine fréquentiel et vice versa.
Le filtrage dans le domaine fréquentiel peut être représenté comme suit:

The steps in filtering are given below.
Dans un premier temps, nous devons effectuer un prétraitement d'une image dans le domaine spatial, c'est-à-dire augmenter son contraste ou sa luminosité
Ensuite, nous prendrons une transformée de Fourier discrète de l'image
Ensuite, nous centrerons la transformée de Fourier discrète, car nous apporterons la transformée de Fourier discrète au centre des coins
Ensuite, nous appliquerons le filtrage, c'est-à-dire que nous multiplierons la transformée de Fourier par une fonction de filtre
Ensuite, nous déplacerons à nouveau le DFT du centre vers les coins
La dernière étape serait de faire l'inverse de la transformée de Fourier discrète, pour ramener le résultat du domaine fréquentiel au domaine spatial
Et cette étape de post-traitement est facultative, tout comme le pré-traitement, dans lequel nous augmentons simplement l'apparence de l'image.
Filtres
Le concept de filtre dans le domaine fréquentiel est le même que le concept de masque en convolution.
Après la conversion d'une image en domaine fréquentiel, certains filtres sont appliqués dans le processus de filtrage pour effectuer différents types de traitement sur une image. Le traitement comprend le flou d'une image, la netteté d'une image, etc.
Les types courants de filtres à ces fins sont:
- Filtre passe-haut idéal
- Filtre passe-bas idéal
- Filtre passe-haut gaussien
- Filtre passe-bas gaussien
Dans le prochain tutoriel, nous aborderons en détail le filtre.