Série de Fourier et transformation
Dans le dernier didacticiel de l'analyse du domaine fréquentiel, nous avons discuté du fait que la série de Fourier et la transformée de Fourier sont utilisées pour convertir un signal en domaine fréquentiel.
Fourier
Fourier était mathématicien en 1822. Il a donné des séries de Fourier et une transformée de Fourier pour convertir un signal en domaine fréquentiel.
Série Fourier
La série de Fourier indique simplement que les signaux périodiques peuvent être représentés en somme des sinus et cosinus lorsqu'ils sont multipliés avec un certain poids.Il indique en outre que les signaux périodiques peuvent être décomposés en signaux supplémentaires avec les propriétés suivantes.
- Les signaux sont des sinus et des cosinus
- Les signaux sont des harmoniques les uns des autres
Il peut être visualisé en images comme
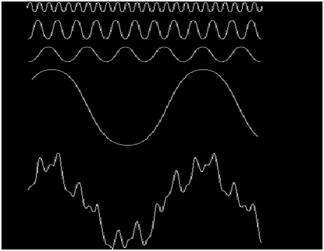
Dans le signal ci-dessus, le dernier signal est en fait la somme de tous les signaux ci-dessus. C'était l'idée du Fourier.
Comment il est calculé
Puisque, comme nous l'avons vu dans le domaine fréquentiel, pour traiter une image dans le domaine fréquentiel, nous devons d'abord la convertir en utilisant le domaine fréquentiel et nous devons prendre l'inverse de la sortie pour la reconvertir en domaine spatial. C'est pourquoi la série de Fourier et la transformée de Fourier ont deux formules. Un pour la conversion et un pour le reconvertir dans le domaine spatial.
Série Fourier
La série de Fourier peut être désignée par cette formule.
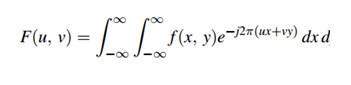
L'inverse peut être calculé par cette formule.
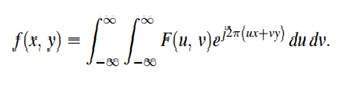
Transformée de Fourier
La transformée de Fourier indique simplement que les signaux non périodiques dont l'aire sous la courbe est finie peuvent également être représentés en intégrales des sinus et cosinus après avoir été multipliés par un certain poids.
La transformée de Fourier a de nombreuses applications étendues qui incluent, la compression d'image (par exemple la compression JPEG), le filtrage et l'analyse d'image.
Différence entre la série de Fourier et la transformation
Bien que la série de Fourier et la transformée de Fourier soient données par Fourier, mais la différence entre elles est que la série de Fourier est appliquée aux signaux périodiques et la transformée de Fourier est appliquée aux signaux non périodiques
Lequel est appliqué sur les images
Maintenant la question est de savoir laquelle est appliquée sur les images, la série de Fourier ou la transformée de Fourier. Eh bien, la réponse à cette question réside dans le fait que ce que sont les images. Les images ne sont pas périodiques. Et comme les images ne sont pas périodiques, la transformée de Fourier est utilisée pour les convertir en domaine fréquentiel.
Transformée de Fourier discrète
Puisque nous avons affaire à des images, et en fait des images numériques, donc pour les images numériques nous travaillerons sur une transformée de Fourier discrète

Considérez le terme de Fourier ci-dessus d'une sinusoïde. Cela comprend trois choses.
- Fréquence spatiale
- Magnitude
- Phase
La fréquence spatiale est directement liée à la luminosité de l'image. L'amplitude de la sinusoïde est directement liée au contraste. Le contraste est la différence entre l'intensité maximale et minimale des pixels. Phase contient les informations de couleur.
La formule de la transformée de Fourier discrète bidimensionnelle est donnée ci-dessous.
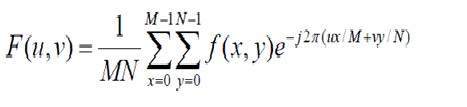
La transformée de Fourier discrète est en fait la transformée de Fourier échantillonnée, elle contient donc des échantillons qui désignent une image. Dans la formule ci-dessus, f (x, y) désigne l'image et F (u, v) désigne la transformée de Fourier discrète. La formule de la transformée de Fourier discrète inverse bidimensionnelle est donnée ci-dessous.
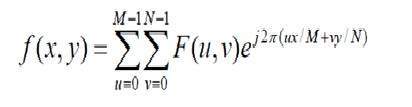
La transformée de Fourier discrète inverse convertit la transformée de Fourier en image
Considérez ce signal
Maintenant, nous allons voir une image, dont nous allons calculer le spectre de magnitude FFT, puis le spectre de magnitude FFT décalé, puis nous prendrons Log de ce spectre décalé.
Image originale

Le spectre de magnitude de la transformée de Fourier

La transformée de Fourier décalée

Le spectre de magnitude décalé
