Transformations d'image

Avant de discuter de ce qu'est la transformation d'image, nous discuterons de ce qu'est une transformation.

Transformation

La transformation est une fonction. Une fonction qui mappe un ensemble à un autre ensemble après avoir effectué certaines opérations.

Système de traitement d'image numérique

Nous avons déjà vu dans les tutoriels d'introduction que dans le traitement d'images numériques, nous développerons un système dont l'entrée serait une image et la sortie serait également une image. Et le système effectuerait un certain traitement sur l'image d'entrée et donnerait sa sortie sous forme d'image traitée. Il est montré ci-dessous.

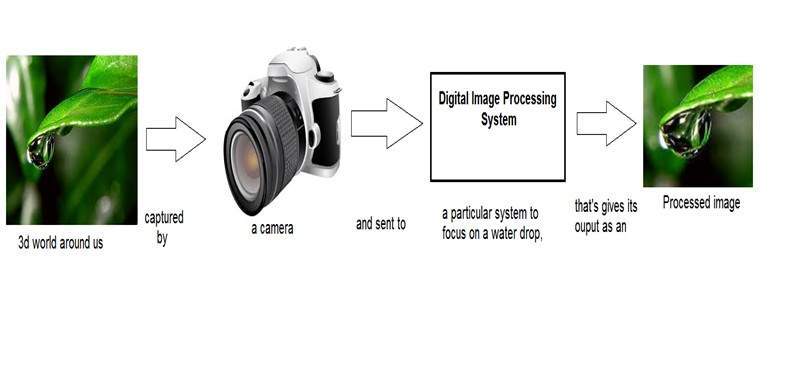
Maintenant, la fonction appliquée à l'intérieur de ce système numérique qui traite une image et la convertit en sortie peut être appelée comme fonction de transformation.

Comme il montre la transformation ou la relation, comment une image1 est convertie en image2.

Transformation d'image.

Considérez cette équation

G (x, y) = T {f (x, y)}

Dans cette équation,

F (x, y) = image d'entrée sur laquelle la fonction de transformation doit être appliquée.

G (x, y) = l'image de sortie ou l'image traitée.

T est la fonction de transformation.

Cette relation entre l'image d'entrée et l'image de sortie traitée peut également être représentée par.

s = T (r)

où r est en fait la valeur de pixel ou l'intensité du niveau de gris de f (x, y) en tout point. Et s est la valeur de pixel ou l'intensité du niveau de gris de g (x, y) à tout moment.

La transformation de niveau de gris de base a été abordée dans notre didacticiel sur les transformations de niveau de gris de base.

Nous allons maintenant discuter de certaines des fonctions de transformation très basiques.

Exemples

Considérez cette fonction de transformation.

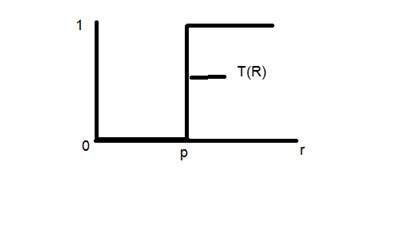
Prenons le point r à 256 et le point p à 127. Considérez cette image comme une image d'un bpp. Cela signifie que nous n'avons que deux niveaux d'intensité qui sont 0 et 1. Dans ce cas, la transformation indiquée par le graphique peut être expliquée par.

Toutes les valeurs d'intensité de pixel inférieures à 127 (point p) sont égales à 0, ce qui signifie noir. Et toutes les valeurs d'intensité de pixel supérieures à 127 sont égales à 1, ce qui signifie blanc. Mais au point exact de 127, il y a un changement soudain de transmission, nous ne pouvons donc pas dire qu'à ce point exact, la valeur serait 0 ou 1.

Mathématiquement, cette fonction de transformation peut être désignée par:

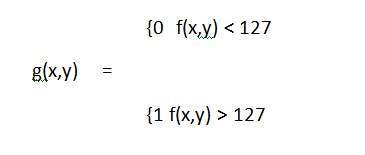
Envisagez une autre transformation comme celle-ci

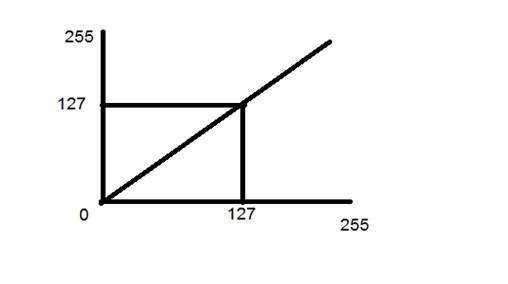
Maintenant, si vous regardez ce graphique particulier, vous verrez une ligne de transition droite entre l'image d'entrée et l'image de sortie.

Il montre que pour chaque pixel ou valeur d'intensité de l'image d'entrée, il y a une même valeur d'intensité de l'image de sortie. Cela signifie que l'image de sortie est une réplique exacte de l'image d'entrée.

Il peut être représenté mathématiquement par:

g (x, y) = f (x, y)

l'image d'entrée et de sortie serait dans ce cas sont montrées ci-dessous.