Introduction au domaine fréquentiel

Nous avons affaire à des images dans de nombreux domaines. Nous traitons maintenant des signaux (images) dans le domaine fréquentiel. Étant donné que cette série de Fourier et ce domaine de fréquence sont purement mathématiques, nous allons donc essayer de minimiser cette partie des mathématiques et de nous concentrer davantage sur son utilisation dans DIP.

Analyse du domaine fréquentiel

Jusqu'à présent, tous les domaines dans lesquels nous avons analysé un signal, nous l'analysons par rapport au temps. Mais dans le domaine fréquentiel, nous n'analysons pas le signal par rapport au temps, mais par rapport à la fréquence.

Différence entre le domaine spatial et le domaine fréquentiel

Dans le domaine spatial, nous traitons les images telles quelles. La valeur des pixels de l'image change par rapport à la scène. Alors que dans le domaine fréquentiel, nous traitons la vitesse à laquelle les valeurs des pixels changent dans le domaine spatial.

Pour simplifier, disons les choses de cette façon.

Domaine spatial

Dans le domaine spatial simple, nous traitons directement la matrice d'image. Alors que dans le domaine fréquentiel, nous traitons une image comme celle-ci.

Domaine de fréquence

Nous transformons d'abord l'image en sa distribution de fréquence. Ensuite, notre système de boîte noire effectue tout le traitement qu'il doit effectuer, et la sortie de la boîte noire dans ce cas n'est pas une image, mais une transformation. Après avoir effectué une transformation inverse, il est converti en une image qui est ensuite visualisée dans le domaine spatial.

Il peut être visualisé en images comme

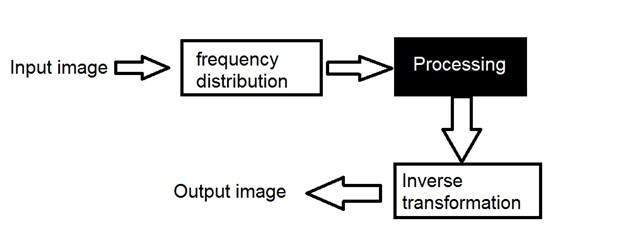
Ici, nous avons utilisé le mot transformation. Qu'est-ce que cela signifie réellement?

Transformation

Un signal peut être converti du domaine temporel au domaine fréquentiel à l'aide d'opérateurs mathématiques appelés transformées. Il existe de nombreux types de transformation qui font cela. Certains d'entre eux sont donnés ci-dessous.