Théorie des réseaux - Circuits équivalents
Si un circuit se compose de deux ou plusieurs éléments passifs similaires et sont connectés exclusivement de type série ou de type parallèle, alors nous pouvons les remplacer par un seul élément passif équivalent. Par conséquent, ce circuit est appelé comme unequivalent circuit.
Dans ce chapitre, discutons des deux circuits équivalents suivants.
- Circuit équivalent en série
- Circuit équivalent parallèle
Circuit équivalent en série
Si des éléments passifs similaires sont connectés series, alors le même courant traversera tous ces éléments. Mais, la tension est divisée entre chaque élément.
Considérer ce qui suit circuit diagram.
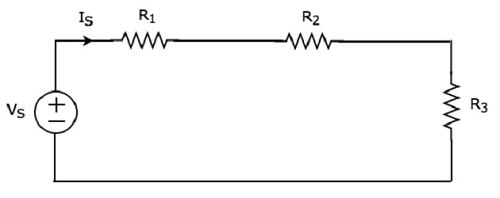
Il possède une seule source de tension (V S ) et trois résistances ayant des résistances de R 1 , R 2 et R 3 . Tous ces éléments sont connectés en série. Le SI actuel traverse tous ces éléments.
Le circuit ci-dessus n'a qu'une seule maille. leKVL equation autour de ce maillage se trouve
$$ V_S = V_1 + V_2 + V_3 $$
Remplacez $ V_1 = I_S R_1, \: V_2 = I_S R_2 $ et $ V_3 = I_S R_3 $ dans l'équation ci-dessus.
$$ V_S = I_S R_1 + I_S R_2 + I_S R_3 $$
$$ \ Flèche droite V_S = I_S (R_1 + R_2 + R_3) $$
L'équation ci-dessus se présente sous la forme $ V_S = I_S R_ {Eq} $ où,
$$ R_ {Eq} = R_1 + R_2 + R_3 $$
le equivalent circuit diagram du circuit donné est illustré dans la figure suivante.
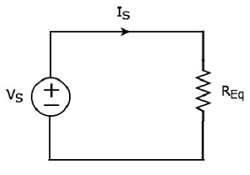
Cela signifie que si plusieurs résistances sont connectées en série, nous pouvons les remplacer par un equivalent resistor. La résistance de cette résistance équivalente est égale à la somme des résistances de toutes ces résistances multiples.
Note 1- Si des inductances 'N' ayant des inductances de L 1 , L 2 , ..., L N sont connectées en série, alors leequivalent inductance sera
$$ L_ {Eq} = L_1 + L_2 + ... + L_N $$
Note 2- Si des condensateurs 'N' ayant des capacités de C 1 , C 2 , ..., C N sont connectés en série, alors leequivalent capacitance sera
$$ \ frac {1} {C_ {Eq}} = \ frac {1} {C_1} + \ frac {1} {C_2} + ... + \ frac {1} {C_N} $$
Circuit équivalent parallèle
Si des éléments passifs similaires sont connectés parallel, alors la même tension sera maintenue à travers chaque élément. Mais le courant traversant chaque élément se divise.
Considérer ce qui suit circuit diagram.

Il possède une seule source de courant (I S ) et trois résistances ayant des résistances de R 1 , R 2 et R 3 . Tous ces éléments sont connectés en parallèle. La tension (V S ) est disponible sur tous ces éléments.
Le circuit ci-dessus n'a qu'un seul nœud principal (P) à l'exception du nœud Ground. leKCL equation à ce nœud principal (P) est
$$ I_S = I_1 + I_2 + I_3 $$
Remplacez $ I_1 = \ frac {V_S} {R_1}, \: I_2 = \ frac {V_S} {R_2} $ et $ I_3 = \ frac {V_S} {R_3} $ dans l'équation ci-dessus.
$$ I_S = \ frac {V_S} {R_1} + \ frac {V_S} {R_2} + \ frac {V_S} {R_3} $$
$$ \ Rightarrow I_S = V_S \ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup $$
$$ \ Rightarrow V_S = I_S \ left [\ frac {1} {\ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup} \ right] $$
L'équation ci-dessus se présente sous la forme de V S = I S R Eq où,
$$ R_ {Eq} = \ frac {1} {\ lgroup \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} \ rgroup} $$
$$ \ frac {1} {R_ {Eq}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} $$
le equivalent circuit diagram du circuit donné est illustré dans la figure suivante.
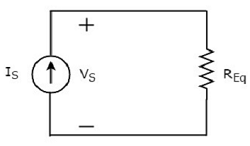
Cela signifie que si plusieurs résistances sont connectées en parallèle, nous pouvons les remplacer par une résistance équivalente. La résistance de ceequivalent resistor est égale à l'inverse de la somme de l'inverse de chaque résistance de toutes ces résistances multiples.
Note 1- Si des inductances 'N' ayant des inductances de L 1 , L 2 , ..., L N sont connectées en parallèle, alors leequivalent inductance sera
$$ \ frac {1} {L_ {Eq}} = \ frac {1} {L_1} + \ frac {1} {L_2} + ... + \ frac {1} {L_N} $$
Note 2- Si des condensateurs 'N' ayant des capacités de C 1 , C 2 , ..., C N sont connectés en parallèle, alors leequivalent capacitance sera
$$ C_ {Eq} = C_1 + C_2 + ... + C_N $$