Théorie des réseaux - Lois de Kirchhoff
Les éléments du réseau peuvent être active ou passivetype. Tout circuit ou réseau électrique contient l'un de ces deux types d'éléments de réseau ou une combinaison des deux.
Maintenant, laissez-nous discuter des deux lois suivantes, qui sont communément appelées Kirchhoff’s laws.
- Loi actuelle de Kirchhoff
- Loi de tension de Kirchhoff
Loi actuelle de Kirchhoff
La loi actuelle de Kirchhoff (KCL) stipule que la somme algébrique des courants quittant (ou entrant) un nœud est égale à zéro.
UNE Nodeest un point où deux ou plusieurs éléments de circuit y sont connectés. Si seulement deux éléments de circuit sont connectés à un nœud, on dit qu'il s'agit d'un nœud simple. Si trois éléments de circuit ou plus sont connectés à un nœud, on dit qu'il estPrincipal Node.
Mathematically, KCL peut être représenté comme
$$ \ displaystyle \ sum \ limits_ {m = 1} ^ M I_m = 0 $$
Où,
Imest le m ième courant de branche quittant le nœud
M est le nombre de branches connectées à un nœud.
La déclaration ci-dessus de KCLpeut également être exprimée comme "la somme algébrique des courants entrant dans un nœud est égale à la somme algébrique des courants quittant un nœud". Vérifions cette affirmation à travers l'exemple suivant.
Exemple
Écrire KCL equation au nœud P de la figure suivante.
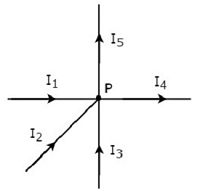
Dans la figure ci-dessus, les courants de dérivation I 1 , I 2 et I 3 sontentering au nœud P. Alors, considérons les signes négatifs pour ces trois courants.
Dans la figure ci-dessus, les courants de dérivation I 4 et I 5 sontleaving du nœud P. Alors, considérons les signes positifs pour ces deux courants.
le KCL equation au nœud P sera
$$ - I_1 - I_2 - I_3 + I_4 + I_5 = 0 $$
$$ \ Rightarrow I_1 + I_2 + I_3 = I_4 + I_5 $$
Dans l'équation ci-dessus, le côté gauche représente la somme des courants entrants, tandis que le côté droit représente la somme des courants sortants.
Dans ce tutoriel, nous considérerons le signe positif lorsque le courant quitte un nœud et le signe négatif lorsqu'il entre dans un nœud. De même, vous pouvez considérer un signe négatif lorsque le courant quitte un nœud et un signe positif lorsqu'il entre dans un nœud. Dans les deux cas, leresult will be same.
Note - KCL est indépendant de la nature des éléments de réseau connectés à un nœud.
Loi de tension de Kirchhoff
La loi de tension de Kirchhoff (KVL) stipule que la somme algébrique des tensions autour d'une boucle ou d'un maillage est égale à zéro.
UNE Loopest un chemin qui se termine au même nœud d'où il a commencé. En revanche, unMesh est une boucle qui ne contient aucune autre boucle à l'intérieur.
Mathématiquement, KVL peut être représenté comme
$$ \ displaystyle \ sum \ limits_ {n = 1} ^ N V_n = 0 $$
Où,
Vnest la tension du n ième élément dans une boucle (maillage).
N est le nombre d'éléments de réseau dans la boucle (maillage).
La déclaration ci-dessus de KVLpeut également être exprimée comme «la somme algébrique des sources de tension est égale à la somme algébrique des chutes de tension présentes dans une boucle». Vérifions cette affirmation à l'aide de l'exemple suivant.
Exemple
Écrire KVL equation autour de la boucle du circuit suivant.
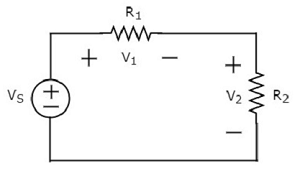
Le schéma ci-dessus se compose d'une source de tension, V S en série avec deux résistances R 1 et R 2 . Les chutes de tension aux bornes des résistances R 1 et R 2 sont respectivement V 1 et V 2 .
Appliquer KVL autour de la boucle.
$$ V_S - V_1 - V_2 = 0 $$
$$ \ Rightarrow V_S = V_1 + V_2 $$
Dans l'équation ci-dessus, le terme de gauche représente une seule source de tension VS. Alors que le côté droit représente lesum of voltage drops. Dans cet exemple, nous n'avons considéré qu'une seule source de tension. C'est pourquoi le côté gauche ne contient qu'un seul terme. Si nous considérons plusieurs sources de tension, alors le côté gauche contient la somme des sources de tension.
Dans ce tutoriel, nous considérons le signe de la tension de chaque élément comme la polarité de la deuxième borne qui est présente lors du déplacement autour de la boucle. De même, vous pouvez considérer le signe de chaque tension comme la polarité de la première borne présente lors du déplacement autour de la boucle. Dans les deux cas, leresult will be same.
Note - KVL est indépendant de la nature des éléments de réseau qui sont présents dans une boucle.