Théorie des réseaux - Guide rapide
Network theoryest l'étude de la résolution des problèmes de circuits électriques ou de réseaux électriques. Dans ce chapitre d'introduction, examinons d'abord la terminologie de base des circuits électriques et les types d'éléments de réseau.
Terminologie de base
Dans la théorie des réseaux, nous rencontrerons fréquemment les termes suivants -
- Circuit électrique
- Réseau électrique
- Current
- Voltage
- Power
Donc, il est impératif que nous rassemblions quelques connaissances de base sur ces termes avant de continuer. Commençons par Circuit électrique.
Circuit électrique
Un circuit électrique contient un chemin fermé pour fournir un flux d'électrons à partir d'une source de tension ou d'une source de courant. Les éléments présents dans un circuit électrique seront enseries connection, parallel connection, ou dans toute combinaison de connexions série et parallèle.
Réseau électrique
Un réseau électrique n'a pas besoin de contenir un chemin fermé pour fournir un flux d'électrons à partir d'une source de tension ou d'une source de courant. Par conséquent, nous pouvons conclure que «tous les circuits électriques sont des réseaux électriques», mais l'inverse n'est pas nécessairement vrai.
Actuel
Le courant "I"s'écoulant à travers un conducteur n'est rien d'autre que le taux temporel d'écoulement de la charge. Mathématiquement, il peut être écrit comme
$$I = \frac{dQ}{dt}$$
Où,
Q est la charge et son unité est Coloumb.
t est le temps et son unité est la seconde.
Par analogie, le courant électrique peut être considéré comme l'écoulement de l'eau à travers un tuyau. Le courant est mesuré en termes deAmpere.
En général, Electron current s'écoule de la borne négative de la source à la borne positive, alors que, Conventional current flux de la borne positive de la source à la borne négative.
Electron current est obtenu grâce au mouvement d'électrons libres, alors que, Conventional currentest obtenu grâce au mouvement des charges positives gratuites. Les deux sont appelés commeelectric current.
Tension
La tension "V"n'est rien d'autre qu'une force électromotrice qui fait circuler la charge (électrons). Mathématiquement, il peut être écrit comme
$$V = \frac{dW}{dQ}$$
Où,
W est l'énergie potentielle et son unité est Joule.
Q est la charge et son unité est Coloumb.
Par analogie, la tension peut être considérée comme la pression de l'eau qui fait couler l'eau dans un tuyau. Il est mesuré en termes deVolt.
Puissance
La puissance "P"n'est rien d'autre que le débit temporel du flux d'énergie électrique. Mathématiquement, il peut être écrit comme
$$P = \frac{dW}{dt}$$
Où,
W est l'énergie électrique et elle est mesurée en termes de Joule.
t est le temps et il est mesuré en secondes.
Nous pouvons réécrire l'équation ci-dessus a
$$P = \frac{dW}{dt} = \frac{dW}{dQ} \times \frac{dQ}{dt} = VI$$
Par conséquent, power n'est rien d'autre que le product de tension V et courant I. Son unité estWatt.
Types d'éléments de réseau
Nous pouvons classer les éléments du réseau en différents types en fonction de certains paramètres. Voici les types d'éléments de réseau -
Éléments actifs et éléments passifs
Éléments linéaires et éléments non linéaires
Éléments bilatéraux et éléments unilatéraux
Éléments actifs et éléments passifs
Nous pouvons classer les éléments du réseau en soit active ou passive basé sur la capacité de fournir de l'énergie.
Active Elementsfournir de l'énergie à d'autres éléments, qui sont présents dans un circuit électrique. Parfois, ils peuvent absorber le pouvoir comme des éléments passifs. Cela signifie que les éléments actifs ont la capacité de fournir et d'absorber de la puissance.Examples: Sources de tension et sources de courant.
Passive Elementsne peuvent pas fournir de puissance (énergie) à d'autres éléments, mais ils peuvent absorber de l'énergie. Cela signifie que ces éléments dissipent de l'énergie sous forme de chaleur ou stockent de l'énergie sous forme de champ magnétique ou de champ électrique.Examples: Résistances, inductances et condensateurs.
Éléments linéaires et éléments non linéaires
Nous pouvons classer les éléments du réseau comme linear ou non-linear basé sur leur caractéristique d'obéir à la propriété de linéarité.
Linear Elements sont les éléments qui montrent une relation linéaire entre la tension et le courant. Examples: Résistances, inductances et condensateurs.
Non-Linear Elements sont ceux qui ne montrent pas de relation linéaire entre la tension et le courant. Examples: Sources de tension et sources de courant.
Éléments bilatéraux et éléments unilatéraux
Les éléments de réseau peuvent également être classés comme bilateral ou unilateral basé sur la direction du courant circulant dans les éléments du réseau.
Bilateral Elements sont les éléments qui permettent le courant dans les deux sens et offrent la même impédance dans les deux sens du courant. Examples: Résistances, inductances et condensateurs.
Le concept des éléments bilatéraux est illustré dans les figures suivantes.
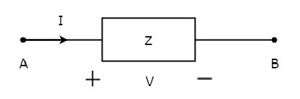
Sur la figure ci-dessus, le courant (I) circule des bornes A à B à travers un élément passif ayant une impédance de Z Ω. C'est le rapport de la tension (V) aux bornes de cet élément entre les bornes A et B et le courant (I).
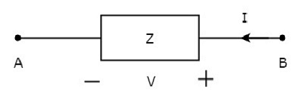
Sur la figure ci-dessus, le courant (I) circule des bornes B vers A à travers un élément passif ayant une impédance de Z Ω. Cela signifie que le courant (–I) circule des bornes A à B.Dans ce cas également, nous obtiendrons la même valeur d'impédance, car le courant et la tension ont des signes négatifs par rapport aux bornes A et B.
Unilateral Elementssont ceux qui permettent le courant dans une seule direction. Par conséquent, ils offrent des impédances différentes dans les deux sens.
Nous avons discuté des types d'éléments de réseau dans le chapitre précédent. Maintenant, identifions lenature of network elements à partir des caractéristiques VI données dans les exemples suivants.
Exemple 1
le V-I characteristics d'un élément de réseau est illustré ci-dessous.
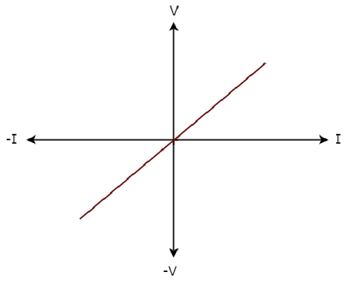
Step 1 - Vérification de l'élément de réseau comme linear ou non-linear.
D'après la figure ci-dessus, la caractéristique VI d'un élément de réseau est une ligne droite passant par l'origine. Par conséquent, c'est unLinear element.
Step 2 - Vérification de l'élément de réseau comme active ou passive.
Les caractéristiques VI données d'un élément de réseau se trouvent dans les premier et troisième quadrants.
dans le first quadrant, les valeurs de la tension (V) et du courant (I) sont positives. Ainsi, les rapports de tension (V) et de courant (I) donnent des valeurs d'impédance positives.
De même, dans le third quadrant, les valeurs de la tension (V) et du courant (I) ont des valeurs négatives. Ainsi, les rapports de tension (V) et de courant (I) produisent des valeurs d'impédance positives.
Puisque les caractéristiques de VI données offrent des valeurs d'impédance positives, l'élément de réseau est un Passive element.
Step 3 - Vérification de l'élément de réseau comme bilateral ou unilateral.
Pour chaque point (I, V) sur les caractéristiques, il existe un point correspondant (-I, -V) sur les caractéristiques données. Par conséquent, l'élément de réseau est unBilateral element.
Par conséquent, les caractéristiques du VI données montrent que l'élément de réseau est un Linear, Passive, et Bilateral element.
Exemple 2
le V-I characteristics d'un élément de réseau est illustré ci-dessous.
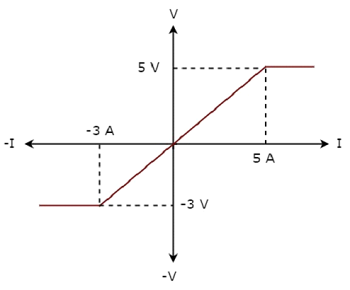
Step 1 - Vérification de l'élément de réseau comme linear ou non-linear.
D'après la figure ci-dessus, les caractéristiques du VI d'un élément de réseau sont une ligne droite uniquement entre les points (-3A, -3V) et (5A, 5V). Au-delà de ces points, les caractéristiques du VI ne suivent pas la relation linéaire. Par conséquent, c'est unNon-linear element.
Step 2 - Vérification de l'élément de réseau comme active ou passive.
Les caractéristiques VI données d'un élément de réseau se trouvent dans les premier et troisième quadrants. Dans ces deux quadrants, les rapports de tension (V) et de courant (I) produisent des valeurs d'impédance positives. Par conséquent, l'élément de réseau est unPassive element.
Step 3 - Vérification de l'élément de réseau comme bilateral or unilateral.
Considérez le point (5A, 5V) sur les caractéristiques. Le point correspondant (-5A, -3V) existe sur les caractéristiques données au lieu de (-5A, -5V). Par conséquent, l'élément de réseau est unUnilateral element.
Par conséquent, les caractéristiques du VI données montrent que l'élément de réseau est un Non-linear, Passive, et Unilateral element.
Active Elementssont les éléments de réseau qui fournissent de l'énergie à d'autres éléments présents dans un circuit électrique. Ainsi, les éléments actifs sont également appelés sources de tension ou de type courant. Nous pouvons classer ces sources dans les deux catégories suivantes -
- Sources indépendantes
- Sources dépendantes
Sources indépendantes
Comme son nom l'indique, les sources indépendantes produisent des valeurs fixes de tension ou de courant et celles-ci ne dépendent d'aucun autre paramètre. Les sources indépendantes peuvent être divisées dans les deux catégories suivantes -
- Sources de tension indépendantes
- Sources de courant indépendantes
Sources de tension indépendantes
Une source de tension indépendante produit une tension constante entre ses deux bornes. Cette tension est indépendante de la quantité de courant qui passe à travers les deux bornes de la source de tension.
Indépendant ideal voltage source et ses caractéristiques VI sont illustrées dans la figure suivante.
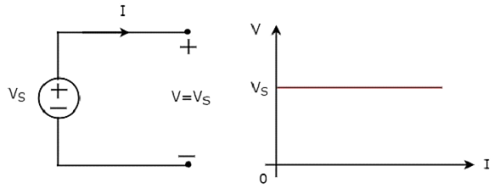
le V-I characteristicsd'une source de tension idéale indépendante est une ligne constante, qui est toujours égale à la tension de source (VS) quelle que soit la valeur du courant (I). Ainsi, la résistance interne d'une source de tension idéale indépendante est de zéro Ohms.
Par conséquent, les sources de tension idéales indépendantes do not exist practically, car il y aura une certaine résistance interne.
Indépendant practical voltage source et ses caractéristiques VI sont illustrées dans la figure suivante.
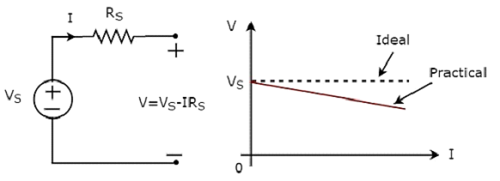
Il existe un écart entre les caractéristiques VI d'une source de tension pratique indépendante et les caractéristiques VI d'une source de tension idéale indépendante. Ceci est dû à la chute de tension à travers la résistance interne (R S ) d'une source de tension pratique indépendante.
Sources de courant indépendantes
Une source de courant indépendante produit un courant constant. Ce courant est indépendant de la tension aux bornes de ses deux bornes. Indépendantideal current source et ses caractéristiques VI sont illustrées dans la figure suivante.

le V-I characteristicsd'une source de courant idéale indépendante est une ligne constante, qui est toujours égale au courant de source (I S ) quelle que soit la valeur de la tension (V). Ainsi, la résistance interne d'une source de courant idéale indépendante est en ohms infinis.
Par conséquent, les sources de courant idéales indépendantes do not exist practically, car il y aura une certaine résistance interne.
Indépendant practical current source et ses caractéristiques VI sont illustrées dans la figure suivante.
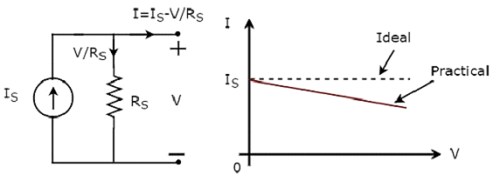
Il existe un écart entre les caractéristiques du VI d'une source de courant pratique indépendante et les caractéristiques du VI d'une source de courant idéale indépendante. Cela est dû à la quantité de courant circulant à travers la résistance de shunt interne (R S ) d'une source de courant pratique indépendante.
Sources dépendantes
Comme son nom l'indique, les sources dépendantes produisent la quantité de tension ou de courant qui dépend d'une autre tension ou d'un autre courant. Les sources dépendantes sont également appeléescontrolled sources. Les sources dépendantes peuvent être divisées dans les deux catégories suivantes -
- Sources de tension dépendantes
- Sources de courant dépendantes
Sources de tension dépendantes
Une source de tension dépendante produit une tension entre ses deux bornes. La quantité de cette tension dépend d'une autre tension ou d'un autre courant. Par conséquent, les sources de tension dépendantes peuvent être classées dans les deux catégories suivantes -
- Source de tension dépendante de la tension (VDVS)
- Source de tension dépendante du courant (CDVS)
Les sources de tension dépendantes sont représentées par les signes «+» et «-» à l'intérieur d'un losange. L'amplitude de la source de tension peut être représentée à l'extérieur de la forme de losange.
Sources de courant dépendantes
Une source de courant dépendante produit un courant. La quantité de ce courant dépend d'une autre tension ou d'un autre courant. Par conséquent, les sources de courant dépendantes peuvent être classées dans les deux catégories suivantes -
- Source de courant dépendant de la tension (VDCS)
- Source de courant dépendant du courant (CDCS)
Les sources de courant dépendantes sont représentées par une flèche à l'intérieur d'une forme de diamant. L'amplitude de la source de courant peut être représentée en dehors de la forme de diamant.
On peut observer ces sources dépendantes ou contrôlées dans des modèles équivalents de transistors.
Technique de transformation de la source
Nous savons qu'il existe deux sources pratiques, à savoir, voltage source et current source. Nous pouvons transformer (convertir) une source en une autre en fonction des besoins, tout en résolvant les problèmes de réseau.
La technique de transformation d'une source en une autre est appelée source transformation technique. Voici les deux transformations sources possibles -
- Source de tension pratique dans une source de courant pratique
- Source de courant pratique dans une source de tension pratique
Source de tension pratique dans une source de courant pratique
La transformation d'une source de tension pratique en une source de courant pratique est illustrée dans la figure suivante
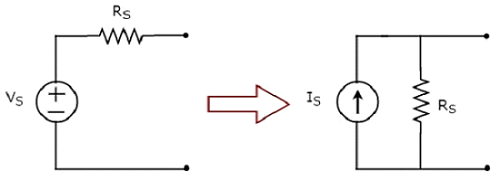
Practical voltage sourcese compose d'une source de tension (V S ) en série avec une résistance (R S ). Cela peut être converti en une source de courant pratique comme indiqué sur la figure. Il se compose d'une source de courant (I S ) en parallèle avec une résistance (R S ).
La valeur de IS sera égal au rapport entre V S et R S . Mathématiquement, il peut être représenté comme
$$I_S = \frac{V_S}{R_S}$$
Source de courant pratique dans une source de tension pratique
La transformation d'une source de courant pratique en une source de tension pratique est illustrée dans la figure suivante.
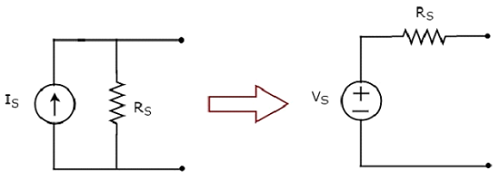
La source de courant pratique consiste en une source de courant (I S ) en parallèle avec une résistance (R S ). Cela peut être converti en une source de tension pratique comme indiqué sur la figure. Il se compose d'une source de tension (V S ) en série avec une résistance (R S ).
La valeur de V S est égale au produit de I S et R S . Mathématiquement, il peut être représenté comme
$$V_S = I_S R_S$$
Dans ce chapitre, nous discuterons en détail des éléments passifs tels que la résistance, l'inductance et le condensateur. Commençons par les résistances.
Résistance
La fonctionnalité principale de la résistance est soit s'oppose, soit limite le flux de courant électrique. Par conséquent, les résistances sont utilisées afin de limiter la quantité de courant et / ou la tension de division (partage).
Laissez le courant traversant la résistance est de I ampères et la tension à travers elle est de V volts. lesymbol de la résistance avec le courant, I et la tension, V sont indiqués dans la figure suivante.
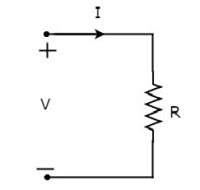
Selon Ohm’s law, la tension aux bornes de la résistance est le produit du courant qui la traverse et de la résistance de cette résistance. Mathematically, il peut être représenté comme
$V = IR$ Equation 1
$\Rightarrow I = \frac{V}{R}$Equation 2
Où, R est la résistance d'une résistance.
À partir de l'équation 2, nous pouvons conclure que le courant traversant la résistance est directement proportionnel à la tension appliquée aux bornes de la résistance et inversement proportionnel à la résistance de la résistance.
Power dans un circuit électrique, l'élément peut être représenté par
$P = VI$Equation 3
Substitut, équation 1 dans l'équation 3.
$P = (IR)I$
$\Rightarrow P = I^2 R$ Equation 4
Substitut, équation 2 dans l'équation 3.
$P = V \lgroup \frac{V}{R} \rgroup$
$\Rightarrow P = \frac{V^2}{R}$ Equation 5
Ainsi, nous pouvons calculer la quantité de puissance dissipée dans la résistance en utilisant l'une des formules mentionnées dans les équations 3 à 5.
Inducteur
En général, les inducteurs auront un nombre de tours. Par conséquent, ils produisent un flux magnétique lorsque le courant le traverse. Ainsi, la quantité de flux magnétique total produit par un inducteur dépend du courant, je le traverse et ils ont une relation linéaire.
Mathematically, il peut s'écrire
$$\Psi \: \alpha \: I$$
$$\Rightarrow \Psi = LI$$
Où,
Ψ est le flux magnétique total
L est l'inductance d'un inducteur
Laissez le courant circulant à travers l'inductance est I ampères et la tension à travers elle est V volts. lesymbolde l'inducteur ainsi que le courant I et la tension V sont indiqués dans la figure suivante.
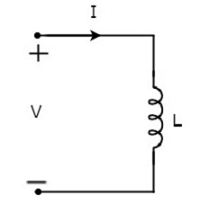
Selon Faraday’s law, la tension aux bornes de l'inductance peut être écrite comme
$$V = \frac{d\Psi}{dt}$$
Remplacez Ψ = LI dans l'équation ci-dessus.
$$V = \frac{d(LI)}{dt}$$
$$\Rightarrow V = L \frac{dI}{dt}$$
$$\Rightarrow I = \frac{1}{L} \int V dt$$
À partir des équations ci-dessus, nous pouvons conclure qu'il existe un linear relationship entre la tension aux bornes de l'inducteur et le courant qui le traverse.
Nous savons que power dans un circuit électrique, l'élément peut être représenté par
$$P = VI$$
Remplacer $V = L \frac{dI}{dt}$ dans l'équation ci-dessus.
$$P = \lgroup L \frac{dI}{dt}\rgroup I$$
$$\Rightarrow P = LI \frac{dI}{dt}$$
En intégrant l'équation ci-dessus, nous obtiendrons le energy stocké dans un inducteur comme
$$W = \frac{1}{2} LI^2$$
Ainsi, l'inducteur stocke l'énergie sous forme de champ magnétique.
Condensateur
En général, un condensateur comporte deux plaques conductrices, séparées par un milieu diélectrique. Si une tension positive est appliquée à travers le condensateur, il stocke une charge positive. De même, si une tension négative est appliquée à travers le condensateur, il stocke une charge négative.
Ainsi, la quantité de charge stockée dans le condensateur dépend de la tension appliquée Và travers et ils ont une relation linéaire. Mathématiquement, il peut être écrit comme
$$Q \: \alpha \: V$$
$$\Rightarrow Q = CV$$
Où,
Q est la charge stockée dans le condensateur.
C est la capacité d'un condensateur.
Laissez le courant circulant à travers le condensateur est de I ampères et la tension à travers lui est de V volts. Le symbole du condensateur ainsi que le courant I et la tension V sont représentés dans la figure suivante.
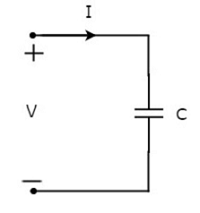
Nous savons que le current n'est rien d'autre que le time rate of flow of charge. Mathématiquement, il peut être représenté comme
$$I = \frac{dQ}{dt}$$
Remplacer $Q = CV$ dans l'équation ci-dessus.
$$I = \frac{d(CV)}{dt}$$
$$\Rightarrow I = C \frac{dV}{dt}$$
$$\Rightarrow V = \frac{1}{C} \int I dt$$
À partir des équations ci-dessus, nous pouvons conclure qu'il existe un linear relationship entre la tension aux bornes du condensateur et le courant qui le traverse.
Nous savons que power dans un circuit électrique, l'élément peut être représenté par
$$P = VI$$
Remplacer $I = C \frac{dV}{dt}$ dans l'équation ci-dessus.
$$P = V \lgroup C \frac{dV}{dt} \rgroup$$
$$\Rightarrow P = CV \frac{dV}{dt}$$
En intégrant l'équation ci-dessus, nous obtiendrons le energy stocké dans le condensateur comme
$$W = \frac{1}{2}CV^2$$
Ainsi, le condensateur stocke l'énergie sous forme de champ électrique.
Les éléments de réseau peuvent être active ou passivetype. Tout circuit ou réseau électrique contient l'un de ces deux types d'éléments de réseau ou une combinaison des deux.
Maintenant, laissez-nous discuter des deux lois suivantes, qui sont communément appelées Kirchhoff’s laws.
- Loi actuelle de Kirchhoff
- Loi de tension de Kirchhoff
Loi actuelle de Kirchhoff
La loi actuelle de Kirchhoff (KCL) stipule que la somme algébrique des courants quittant (ou entrant) un nœud est égale à zéro.
UNE Nodeest un point où deux ou plusieurs éléments de circuit y sont connectés. Si seulement deux éléments de circuit sont connectés à un nœud, alors on dit qu'il s'agit d'un nœud simple. Si trois éléments de circuit ou plus sont connectés à un nœud, on dit qu'il estPrincipal Node.
Mathematically, KCL peut être représenté comme
$$\displaystyle\sum\limits_{m=1}^M I_m = 0$$
Où,
Imest le m ième courant de branche quittant le nœud.
M est le nombre de branches connectées à un nœud.
La déclaration ci-dessus de KCLpeut également être exprimée comme "la somme algébrique des courants entrant dans un nœud est égale à la somme algébrique des courants quittant un nœud". Vérifions cette affirmation à travers l'exemple suivant.
Exemple
Écrire KCL equation au nœud P de la figure suivante.
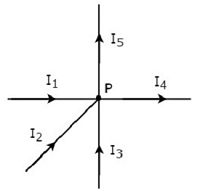
Dans la figure ci-dessus, les courants de dérivation I 1 , I 2 et I 3 sontentering au nœud P. Alors, considérons les signes négatifs pour ces trois courants.
Dans la figure ci-dessus, les courants de dérivation I 4 et I 5 sontleaving à partir du nœud P. Alors, considérons les signes positifs pour ces deux courants.
le KCL equation au nœud P sera
$$- I_1 - I_2 - I_3 + I_4 + I_5 = 0$$
$$\Rightarrow I_1 + I_2 + I_3 = I_4 + I_5$$
Dans l'équation ci-dessus, le côté gauche représente la somme des courants entrants, tandis que le côté droit représente la somme des courants sortants.
Dans ce tutoriel, nous considérerons le signe positif lorsque le courant quitte un nœud et le signe négatif lorsqu'il entre dans un nœud. De même, vous pouvez considérer un signe négatif lorsque le courant quitte un nœud et un signe positif lorsqu'il entre dans un nœud. Dans les deux cas, leresult will be same.
Note - KCL est indépendant de la nature des éléments de réseau connectés à un nœud.
Loi de tension de Kirchhoff
La loi de tension de Kirchhoff (KVL) stipule que la somme algébrique des tensions autour d'une boucle ou d'un maillage est égale à zéro.
UNE Loopest un chemin qui se termine au même nœud d'où il a commencé. En revanche, unMesh est une boucle qui ne contient aucune autre boucle à l'intérieur.
Mathématiquement, KVL peut être représenté comme
$$\displaystyle\sum\limits_{n=1}^N V_n = 0$$
Où,
Vnest la tension du n ième élément dans une boucle (maillage).
N est le nombre d'éléments de réseau dans la boucle (maillage).
La déclaration ci-dessus de KVLpeut également être exprimée comme «la somme algébrique des sources de tension est égale à la somme algébrique des chutes de tension présentes dans une boucle». Vérifions cette affirmation à l'aide de l'exemple suivant.
Exemple
Écrire KVL equation autour de la boucle du circuit suivant.
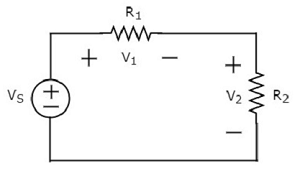
Le schéma ci-dessus se compose d'une source de tension, V S en série avec deux résistances R 1 et R 2 . Les chutes de tension aux bornes des résistances R 1 et R 2 sont respectivement V 1 et V 2 .
Appliquer KVL autour de la boucle.
$$V_S - V_1 - V_2 = 0$$
$$\Rightarrow V_S = V_1 + V_2$$
Dans l'équation ci-dessus, le terme de gauche représente une seule source de tension VS. Alors que le côté droit représente lesum of voltage drops. Dans cet exemple, nous n'avons considéré qu'une seule source de tension. C'est pourquoi le côté gauche ne contient qu'un seul terme. Si nous considérons plusieurs sources de tension, alors le côté gauche contient la somme des sources de tension.
Dans ce tutoriel, nous considérons le signe de la tension de chaque élément comme la polarité de la deuxième borne qui est présente lors du déplacement autour de la boucle. De même, vous pouvez considérer le signe de chaque tension comme la polarité de la première borne présente lors du déplacement autour de la boucle. Dans les deux cas, leresult will be same.
Note - KVL est indépendant de la nature des éléments de réseau qui sont présents dans une boucle.
Dans ce chapitre, discutons des deux principes suivants de division des grandeurs électriques.
- Principe de la division actuelle
- Principe de division de tension
Principe de la division actuelle
Lorsque deux éléments passifs ou plus sont connectés en parallèle, la quantité de courant qui traverse chaque élément devient divided (partagés) entre eux à partir du courant qui entre dans le nœud.
Considérer ce qui suit circuit diagram.
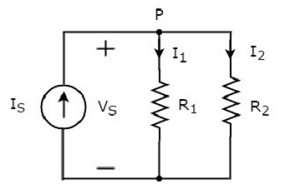
Le schéma de circuit ci-dessus se compose d'une source de courant d'entrée IS en parallèle avec deux résistances R1 et R2. La tension à travers chaque élément estVS. Les courants traversant les résistancesR1 et R2 sont I1 et I2 respectivement.
le KCL equation au nœud P sera
$$I_S = I_1 + I_2$$
Remplacer $I_1 = \frac{V_S}{R_1}$ et $I_2 = \frac{V_S}{R_2}$ dans l'équation ci-dessus.
$$I_S = \frac{V_S}{R_1} + \frac{V_S}{R_2} = V_S \lgroup \frac {R_2 + R_1 }{R_1 R_2} \rgroup$$
$$\Rightarrow V_S = I_S \lgroup \frac{R_1R_2}{R_1 + R_2} \rgroup$$
Remplacez la valeur de V S dans$I_1 = \frac{V_S}{R_1}$.
$$I_1 = \frac{I_S}{R_1}\lgroup \frac{R_1 R_2}{R_1 + R_2} \rgroup$$
$$\Rightarrow I_1 = I_S\lgroup \frac{R_2}{R_1 + R_2} \rgroup$$
Remplacez la valeur de V S dans$I_2 = \frac{V_S}{R_2}$.
$$I_2 = \frac{I_S}{R_2} \lgroup \frac{R_1 R_2}{R_1 + R_2} \rgroup$$
$$\Rightarrow I_2 = I_S \lgroup \frac{R_1}{R_1 + R_2} \rgroup$$
À partir des équations de I 1 et I 2 , nous pouvons généraliser que le courant traversant tout élément passif peut être trouvé en utilisant la formule suivante.
$$I_N = I_S \lgroup \frac{Z_1\rVert Z_2 \rVert...\rVert Z_{N-1}}{Z_1 + Z_2 + ... + Z_N}\rgroup$$
Ceci est connu comme current division principle et il est applicable, lorsque deux ou plusieurs éléments passifs sont connectés en parallèle et qu'un seul courant entre dans le nœud.
Où,
I N est le courant traversant l'élément passif de la N ième branche.
I S est le courant d'entrée, qui entre dans le nœud.
Z 1 , Z 2 ,…, Z N sont les impédances de 1 ère branche, 2 ème branche,…, N ème branche respectivement.
Principe de division de tension
Lorsque deux éléments passifs ou plus sont connectés en série, la quantité de tension présente à travers chaque élément devient divided (partagé) entre eux à partir de la tension disponible sur toute cette combinaison.
Considérer ce qui suit circuit diagram.
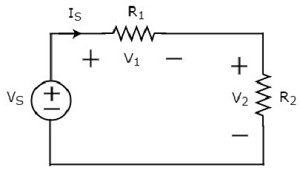
Le schéma ci-dessus se compose d'une source de tension, V S en série avec deux résistances R 1 et R 2 . Le courant circulant à travers ces éléments est I S . Les chutes de tension aux bornes des résistances R 1 et R 2 sont respectivement V 1 et V 2 .
le KVL equation autour de la boucle sera
$$V_S = V_1 + V_2$$
Remplacez V 1 = I S R 1 et V 2 = I S R 2 dans l'équation ci-dessus
$$V_S = I_S R_1 + I_S R_2 = I_S(R_1 + R_2)$$
$$I_S = \frac{V_S}{R_1 + R_2}$$
Remplacez la valeur de I S dans V 1 = I S R 1 .
$$V_1 = \lgroup \frac {V_S}{R_1 + R_2} \rgroup R_1$$
$$\Rightarrow V_1 = V_S \lgroup \frac {R_1}{R_1 + R_2} \rgroup$$
Remplacez la valeur de I S dans V 2 = I S R 2 .
$$V_2 = \lgroup \frac {V_S}{R_1 + R_2} \rgroup R_2$$
$$\Rightarrow V_2 = V_S \lgroup \frac {R_2}{R_1 + R_2} \rgroup$$
À partir des équations de V 1 et V 2 , nous pouvons généraliser que la tension aux bornes de tout élément passif peut être trouvée en utilisant la formule suivante.
$$V_N = V_S \lgroup \frac {Z_N}{Z_1 + Z_2 +....+ Z_N}\rgroup$$
Ceci est connu comme voltage division principle et il est applicable, lorsque deux ou plusieurs éléments passifs sont connectés en série et qu'une seule tension est disponible dans toute la combinaison.
Où,
V N est la tension aux bornes du N ème élément passif.
V S est la tension d'entrée, qui est présente dans toute la combinaison d'éléments passifs en série.
Z 1 , Z 2 ,…, Z 3 sont respectivement les impédances du 1 er élément passif, du 2 ème élément passif,…, du N ème élément passif.
Il existe deux méthodes de base utilisées pour résoudre tout réseau électrique: Nodal analysis et Mesh analysis. Dans ce chapitre, parlons de laNodal analysis méthode.
Dans l'analyse nodale, nous considérerons les tensions des nœuds par rapport à la terre. Par conséquent, l'analyse nodale est également appeléeNode-voltage method.
Procédure d'analyse nodale
Suivez ces étapes lors de la résolution de tout réseau ou circuit électrique à l'aide de l'analyse nodale.
Step 1 - Identifier le principal nodes et choisissez l'un d'entre eux comme reference node. Nous traiterons ce nœud de référence comme le sol.
Step 2 - Étiqueter le node voltages par rapport à Ground à partir de tous les nœuds principaux sauf le nœud de référence.
Step 3 - Ecrire nodal equationsà tous les nœuds principaux à l'exception du nœud de référence. L'équation nodale est obtenue en appliquant d'abord KCL, puis la loi d'Ohm.
Step 4 - Résolvez les équations nodales obtenues à l'étape 3 afin d'obtenir les tensions des nœuds.
Maintenant, nous pouvons trouver le courant traversant n'importe quel élément et la tension à travers n'importe quel élément présent dans le réseau donné en utilisant les tensions de nœud.
Exemple
Trouvez le courant traversant la résistance de 20 Ω du circuit suivant en utilisant Nodal analysis.
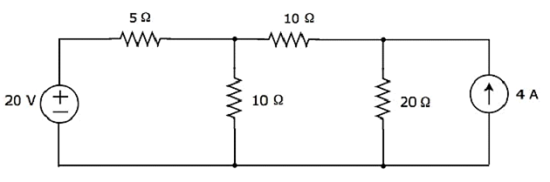
Step 1 - Il y a three principle nodesdans le circuit ci-dessus. Ceux-ci sont étiquetés comme 1, 2 et 3 dans la figure suivante.
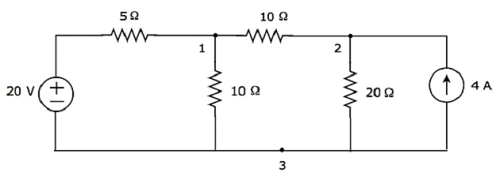
Dans la figure ci-dessus, considérez node 3 comme nœud de référence (Ground).
Step 2- Les tensions aux nœuds, V 1 et V 2 , sont indiquées dans la figure suivante.
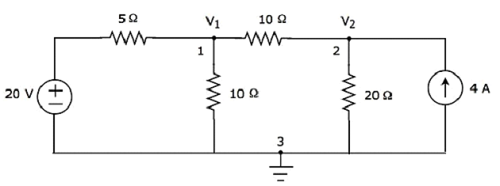
Sur la figure ci-dessus, V 1 est la tension du nœud 1 par rapport à la terre et V 2 est la tension du nœud 2 par rapport à la terre.
Step 3 - Dans ce cas, nous obtiendrons two nodal equations, car il y a deux nœuds principaux, 1 et 2, autres que Ground. Lorsque nous écrivons les équations nodales à un nœud, supposons que tous les courants partent du nœud pour lequel le sens du courant n'est pas mentionné et que la tension de ce nœud est supérieure aux autres tensions de nœud dans le circuit.
le nodal equation au nœud 1 est
$$\frac{V_1 - 20}{5} + \frac{V_1}{10} + \frac{V_1 - V_2}{10} = 0$$
$$\Rightarrow \frac{2 V_1 - 40 + V_1 + V_1 - V_2}{10} = 0$$
$$\Rightarrow 4V_1 - 40 - V_2 = 0$$
$\Rightarrow V_2 = 4V_1 - 40$ Equation 1
le nodal equation au nœud 2 est
$$-4 + \frac{V_2}{20} + \frac{V_2 - V_1}{10} = 0$$
$$\Rightarrow \frac{-80 + V_2 + 2V_2 - 2V_2}{20} = 0$$
$\Rightarrow 3V_2 − 2V_1 = 80$ Equation 2
Step 4- Trouver les tensions de nœud, V 1 et V 2 en résolvant l'équation 1 et l'équation 2.
Remplacez l'équation 1 dans l'équation 2.
$$3(4 V_1 - 40) - 2 V_1 = 80$$
$$\Rightarrow 12 V_1 - 120 - 2V_1 =80$$
$$\Rightarrow 10 V_1 = 200$$
$$\Rightarrow V_1 = 20V$$
Remplacez V 1 = 20 V dans l'équation 1.
$$V_2 = 4(20) - 40$$
$$\Rightarrow V_2 = 40V$$
Donc, nous avons les tensions de nœud V 1 et V 2 comme20 V et 40 V respectivement.
Step 5- La tension aux bornes de la résistance de 20 Ω n'est rien d'autre que la tension du nœud V 2 et elle est égale à 40 V. Maintenant, nous pouvons trouver le courant traversant la résistance de 20 Ω en utilisant la loi d'Ohm.
$$I_{20 \Omega} = \frac{V_2}{R}$$
Remplacez les valeurs de V 2 et R dans l'équation ci-dessus.
$$I_{20 \Omega} = \frac{40}{20}$$
$$\Rightarrow I_{20 \Omega} = 2A$$
Par conséquent, le courant traversant la résistance de 20 Ω d'un circuit donné est 2 A.
Note- De l'exemple ci-dessus, nous pouvons conclure que nous devons résoudre 'n' équations nodales, si le circuit électrique a 'n' nœuds principaux (sauf le nœud de référence). Par conséquent, nous pouvons choisir l'analyse nodale lorsque lenumber of principal nodes (sauf noeud de référence) est inférieur au nombre de mailles de tout circuit électrique.
Dans l'analyse de maillage, nous considérerons les courants circulant à travers chaque maillage. Par conséquent, l'analyse de maillage est également appeléeMesh-current method.
UNE branchest un chemin qui relie deux nœuds et contient un élément de circuit. Si une branche appartient à un seul maillage, alors le courant de branche sera égal au courant de maillage.
Si une branche est commune à deux mailles, alors le courant de branche sera égal à la somme (ou à la différence) de deux courants de maillage, lorsqu'ils sont dans le même sens (ou dans le sens opposé).
Procédure d'analyse du maillage
Suivez ces étapes lors de la résolution de tout réseau ou circuit électrique à l'aide de l'analyse de maillage.
Step 1 - Identifier le meshes et étiquetez les courants de maillage dans le sens horaire ou anti-horaire.
Step 2 - Observez la quantité de courant qui traverse chaque élément en termes de courants de maillage.
Step 3 - Ecrire mesh equationsà tous les maillages. L'équation de maillage est obtenue en appliquant d'abord KVL, puis la loi d'Ohm.
Step 4 - Résoudre les équations de maillage obtenues à l'étape 3 afin d'obtenir le mesh currents.
Maintenant, nous pouvons trouver le courant traversant n'importe quel élément et la tension à travers n'importe quel élément présent dans le réseau donné en utilisant des courants de maillage.
Exemple
Trouvez la tension aux bornes de la résistance de 30 Ω en utilisant Mesh analysis.
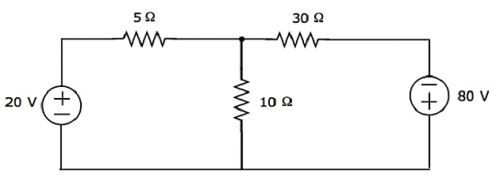
Step 1- Il y a deux mailles dans le circuit ci-dessus. lemesh currentsI 1 et I 2 sont considérés dans le sens des aiguilles d'une montre. Ces courants de maillage sont illustrés dans la figure suivante.
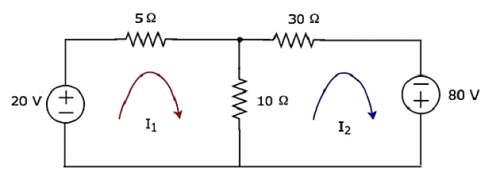
Step 2- Le courant de maillage I 1 traverse une source de tension de 20 V et une résistance de 5 Ω. De même, le courant de maillage I 2 circule à travers une résistance de 30 Ω et une source de tension -80 V. Mais, la différence de deux courants de maillage, I 1 et I 2 , traverse la résistance de 10 Ω, car c'est la branche commune de deux mailles.
Step 3 - Dans ce cas, nous obtiendrons two mesh equationscar il y a deux mailles dans le circuit donné. Lorsque nous écrivons les équations de maillage, supposons que le courant de maillage de ce maillage particulier est supérieur à tous les autres courants de maillage du circuit.
le mesh equation du premier maillage est
$$20 - 5I_1 -10(I_1 - I_2) = 0$$
$$\Rightarrow 20 - 15I_1 + 10I_2 = 0$$
$$\Rightarrow 10I_2 = 15I_1 - 20$$
Divisez l'équation ci-dessus par 5.
$$2I_2 = 3I_1 - 4$$
Multipliez l'équation ci-dessus par 2.
$4I_2 = 6I_1 - 8$ Equation 1
le mesh equation du deuxième maillage est
$$-10(I_2 - I_1) - 30I_2 + 80 = 0$$
Divisez l'équation ci-dessus par 10.
$$-(I_2 - I_1) - 3I_2 + 8 = 0$$
$$\Rightarrow -4I_2 + I_1 + 8 = 0$$
$4I_2 = I_1 + 8$ Equation 2
Step 4- Trouver les courants de maillage I 1 et I 2 en résolvant l'équation 1 et l'équation 2.
Les termes de gauche de l'équation 1 et de l'équation 2 sont les mêmes. Par conséquent, assimilez les termes de droite de l'équation 1 et de l'équation 2 afin de trouver la valeur de I 1 .
$$6I_1 - 8 = I_1 + 8$$
$$\Rightarrow 5I_1 = 16$$
$$\Rightarrow I_1 = \frac{16}{5} A$$
Remplacez la valeur I 1 dans l'équation 2.
$$4I_2 = \frac{16}{5} + 8$$
$$\Rightarrow 4I_2 = \frac{56}{5}$$
$$\Rightarrow I_2 = \frac{14}{5} A$$
Donc, nous avons les courants de maillage I 1 et I 2 comme$\mathbf{\frac{16}{5}}$ A et $\mathbf{\frac{14}{5}}$ A respectivement.
Step 5- Le courant traversant la résistance de 30 Ω n'est rien d'autre que le courant de maillage I 2 et il est égal à$\frac{14}{5}$ A. Maintenant, nous pouvons trouver la tension à travers la résistance de 30 Ω en utilisant la loi d'Ohm.
$$V_{30 \Omega} = I_2 R$$
Remplacez les valeurs de I 2 et R dans l'équation ci-dessus.
$$V_{30 \Omega} = \lgroup \frac{14}{5} \rgroup 30$$
$$\Rightarrow V_{30 \Omega} = 84V$$
Par conséquent, la tension aux bornes de la résistance de 30 Ω du circuit donné est 84 V.
Note 1- A partir de l'exemple ci-dessus, nous pouvons conclure que nous devons résoudre les équations de maillage 'm', si le circuit électrique a des mailles 'm'. C'est pourquoi on peut choisir l'analyse de maillage lorsque le nombre de mailles est inférieur au nombre de nœuds principaux (sauf le nœud de référence) de n'importe quel circuit électrique.
Note 2 - On peut choisir soit l'analyse nodale, soit l'analyse de maillage, lorsque le nombre de mailles est égal au nombre de nœuds principaux (sauf le nœud de référence) dans n'importe quel circuit électrique.
Si un circuit se compose de deux ou plusieurs éléments passifs similaires et sont connectés exclusivement de type série ou parallèle, nous pouvons les remplacer par un seul élément passif équivalent. Par conséquent, ce circuit est appelé comme unequivalent circuit.
Dans ce chapitre, discutons des deux circuits équivalents suivants.
- Circuit équivalent en série
- Circuit équivalent parallèle
Circuit équivalent en série
Si des éléments passifs similaires sont connectés series, alors le même courant traversera tous ces éléments. Mais, la tension est divisée entre chaque élément.
Considérer ce qui suit circuit diagram.
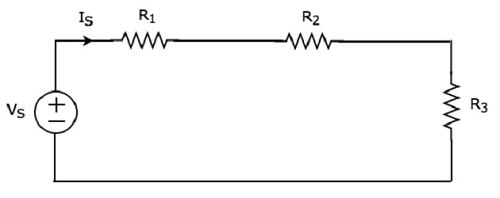
Il possède une seule source de tension (V S ) et trois résistances ayant des résistances de R 1 , R 2 et R 3 . Tous ces éléments sont connectés en série. Le SI actuel traverse tous ces éléments.
Le circuit ci-dessus n'a qu'une seule maille. leKVL equation autour de ce maillage se trouve
$$V_S = V_1 + V_2 + V_3$$
Remplacer $V_1 = I_S R_1, \: V_2 = I_S R_2$ et $V_3 = I_S R_3$ dans l'équation ci-dessus.
$$V_S = I_S R_1 + I_S R_2 + I_S R_3$$
$$\Rightarrow V_S = I_S(R_1 + R_2 + R_3)$$
L'équation ci-dessus est sous la forme de $V_S = I_S R_{Eq}$ où,
$$R_{Eq} = R_1 + R_2 + R_3$$
le equivalent circuit diagram du circuit donné est illustré dans la figure suivante.
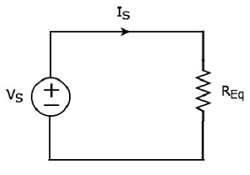
Cela signifie que si plusieurs résistances sont connectées en série, nous pouvons les remplacer par un equivalent resistor. La résistance de cette résistance équivalente est égale à la somme des résistances de toutes ces résistances multiples.
Note 1- Si des inductances 'N' ayant des inductances de L 1 , L 2 , ..., L N sont connectées en série, alors leequivalent inductance sera
$$L_{Eq} = L_1 + L_2 + ... + L_N$$
Note 2- Si des condensateurs 'N' ayant des capacités de C 1 , C 2 , ..., C N sont connectés en série, alors leequivalent capacitance sera
$$\frac{1}{C_{Eq}} = \frac{1}{C_1} + \frac{1}{C_2} + ... + \frac{1}{C_N}$$
Circuit équivalent parallèle
Si des éléments passifs similaires sont connectés parallel, alors la même tension sera maintenue à travers chaque élément. Mais, le courant traversant chaque élément se divise.
Considérer ce qui suit circuit diagram.

Il possède une seule source de courant (I S ) et trois résistances ayant des résistances de R 1 , R 2 et R 3 . Tous ces éléments sont connectés en parallèle. La tension (V S ) est disponible sur tous ces éléments.
Le circuit ci-dessus n'a qu'un seul nœud principal (P) à l'exception du nœud de masse. leKCL equation à ce nœud principal (P) est
$$I_S = I_1 + I_2 + I_3$$
Remplacer $I_1 = \frac{V_S}{R_1}, \: I_2 = \frac{V_S}{R_2}$ et $I_3 = \frac{V_S}{R_3}$ dans l'équation ci-dessus.
$$I_S = \frac{V_S}{R_1} + \frac{V_S}{R_2} + \frac{V_S}{R_3}$$
$$\Rightarrow I_S = V_S \lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup$$
$$\Rightarrow V_S = I_S\left [ \frac{1}{\lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup} \right ]$$
L'équation ci-dessus est sous la forme de V S = I S R Eq où,
$$R_{Eq} = \frac{1}{\lgroup \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} \rgroup}$$
$$\frac{1}{R_{Eq}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$$
le equivalent circuit diagram du circuit donné est illustré dans la figure suivante.
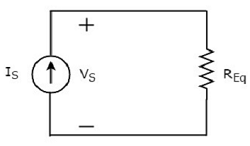
Cela signifie que si plusieurs résistances sont connectées en parallèle, nous pouvons les remplacer par une résistance équivalente. La résistance de ceequivalent resistor est égal à l'inverse de la somme de l'inverse de chaque résistance de toutes ces résistances multiples.
Note 1- Si des inductances 'N' ayant des inductances de L 1 , L 2 , ..., L N sont connectées en parallèle, alors leequivalent inductance sera
$$\frac{1}{L_{Eq}} = \frac{1}{L_1} + \frac{1}{L_2} + ... + \frac{1}{L_N}$$
Note 2- Si des condensateurs 'N' ayant des capacités de C 1 , C 2 , ..., C N sont connectés en parallèle, alors leequivalent capacitance sera
$$C_{Eq} = C_1 + C_2 + ... + C_N$$
Dans le chapitre précédent, nous avons discuté des circuits équivalents de combinaison en série et de combinaison en parallèle individuellement. Dans ce chapitre, résolvons un problème d'exemple en considérant à la fois des combinaisons en série et en parallèle d'éléments passifs similaires.
Exemple
Trouvons le equivalent resistance aux bornes A et B du réseau électrique suivant.

Nous obtiendrons la résistance équivalente aux bornes A et B en minimisant le réseau ci-dessus en une seule résistance entre ces deux bornes. Pour cela, nous devonsidentify the combination of resistors qui sont connectés en série et en parallèle, puis trouvent la résistance équivalente de la forme respective à chaque étape.
Le réseau électrique donné est modified sous la forme suivante, comme illustré dans la figure suivante.
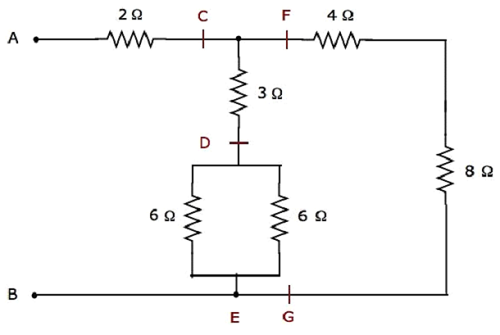
Dans la figure ci-dessus, les lettres C à G sont utilisées pour étiqueter divers terminaux.
Step 1 - Dans le réseau ci-dessus, deux 6 Ω resistors sont connectés en parallel. Ainsi, la résistance équivalente entre D & E sera de 3 Ω. Ceci peut être obtenu en faisant la simplification suivante.
$$R_{DE} = \frac{6 \times 6}{6 + 6} = \frac{36}{12} = 3 \Omega$$
Dans le réseau ci-dessus, les résistances 4 Ω et 8 Ω sont connectés en series. Ainsi, la résistance équivalente entre F et G sera de 12 Ω. Ceci peut être obtenu en faisant la simplification suivante.
$$R_{FG} = 4 + 8 = 12 \Omega$$
Step 2 - L'électricité simplifiée network after Step 1 est illustré dans la figure suivante.
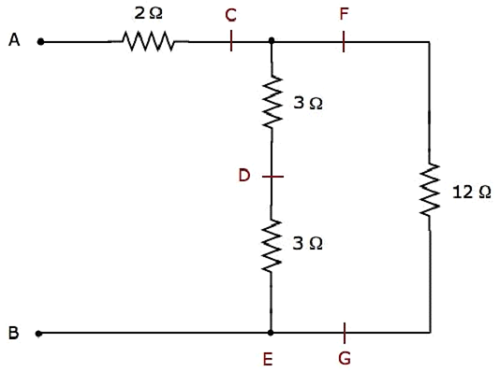
Dans le réseau ci-dessus, deux 3 Ω resistors sont connectés en series. Ainsi, la résistance équivalente entre C et E sera6 Ω. Ceci peut être obtenu en faisant la simplification suivante.
$$R_{CE} = 3 + 3 = 6 \Omega$$
Step 3 - L'électricité simplifiée network after Step 2 est illustré dans la figure suivante.

Dans le réseau ci-dessus, les résistances 6 Ω et 12 Ω sont connectés en parallel. Ainsi, la résistance équivalente entre C et B sera de 4 Ω. Ceci peut être obtenu en faisant la simplification suivante.
$$R_{CB} = \frac{6 \times 12}{6 + 12} = \frac{72}{18} = 4 \Omega$$
Step 4 - L'électricité simplifiée network after Step 3 est illustré dans la figure suivante.
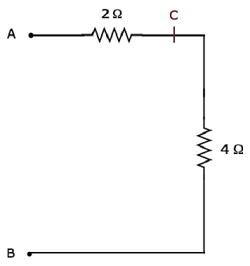
Dans le réseau ci-dessus, les résistances 2 Ω et 4 Ω sont connectés en seriesentre les bornes A et B. Ainsi, la résistance équivalente entre A et B sera de 6 Ω. Ceci peut être obtenu en faisant la simplification suivante.
$$R_{AB} = 2 + 4 = 6 \Omega$$
Par conséquent, la résistance équivalente entre les bornes A et B du réseau électrique donné est 6 Ω.
Dans le chapitre précédent, nous avons discuté d'un exemple de résistance équivalente liée à un problème. Là, nous avons calculé leequivalent resistanceentre les bornes A et B du réseau électrique donné facilement. Parce qu'à chaque étape, nous avons obtenu la combinaison de résistances connectées en série ou en parallèle.
Cependant, dans certaines situations, il est difficile de simplifier le réseau en suivant l'approche précédente. Par exemple, les résistances connectées sous forme delta (δ) ou en forme d'étoile. Dans de telles situations, nous devonsconvertle réseau d'une forme à l'autre afin de le simplifier davantage en utilisant des combinaisons en série ou en parallèle. Dans ce chapitre, parlons de laDelta to Star Conversion.
Réseau Delta
Considérer ce qui suit delta network comme indiqué dans la figure suivante.
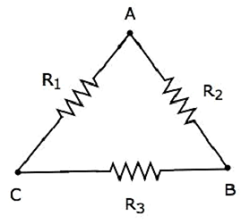
Les équations suivantes représentent le equivalent resistance entre deux terminaux du réseau delta, lorsque le troisième terminal est maintenu ouvert.
$$R_{AB} = \frac{(R_1 + R_3)R_2}{R_1 + R_2 + R_3}$$
$$R_{BC} = \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$$
$$R_{CA} = \frac{(R_2 + R_3)R_1}{R_1 + R_2 + R_3}$$
Réseau Star
La figure suivante montre le equivalent star network correspondant au réseau delta ci-dessus.
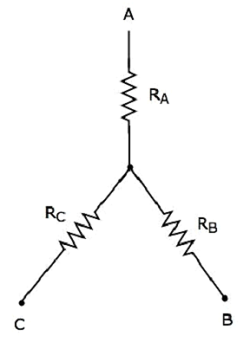
Les équations suivantes représentent le equivalent resistance entre deux terminaux du réseau en étoile, lorsque le troisième terminal est maintenu ouvert.
$$R_{AB} = R_A + R_B$$
$$R_{BC} = R_B + R_C$$
$$R_{CA} = R_C + R_A$$
Résistances Star Network en termes de Résistances Delta Network
Nous obtiendrons les équations suivantes en assimilant les termes de droite des équations ci-dessus pour lesquelles les termes de gauche sont les mêmes.
$R_A + R_B = \frac{(R_1 + R_3)R_2}{R_1 + R_2 + R_3}$ Equation 1
$R_B + R_C = \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$ Equation 2
$R_C + R_A = \frac{(R_2 + R_3)R_1}{R_1 + R_2 + R_3}$ Equation 3
En ajoutant les trois équations ci-dessus, nous obtiendrons
$$2(R_A + R_B + R_C) = \frac{2(R_1 R_2 + R_2 R_3 + R_3 R_1)}{R_1 + R_2 + R_3}$$
$\Rightarrow R_A + R_B + R_C = \frac{R_1 R_2 + R_2 R_3 + R_3 R_1}{R_1 + R_2 + R_3}$ Equation 4
Soustrayez l'équation 2 de l'équation 4.
$R_A + R_B + R_C - (R_B + R_C) = \frac{R_1 R_2 + R_2 R_3 + R_3 R_1}{R_1 + R_2 + R_3} - \frac{(R_1 + R_2)R_3}{R_1 + R_2 + R_3}$
$$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$$
En soustrayant l'équation 3 de l'équation 4, nous obtiendrons
$$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$$
En soustrayant l'équation 1 de l'équation 4, nous obtiendrons
$$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$$
En utilisant les relations ci-dessus, nous pouvons trouver les résistances du réseau en étoile à partir des résistances du réseau delta. De cette façon, nous pouvons convertir undelta network dans une star network.
Exemple
Calculons le resistances of star network, qui sont équivalentes à celle du réseau delta comme indiqué dans la figure suivante.
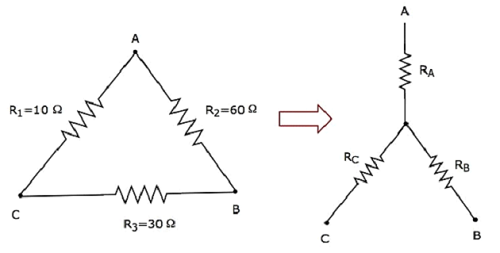
Compte tenu du resistances of delta networkcomme R 1 = 10 Ω, R 2 = 60 Ω et R 3 = 30 Ω.
On connaît les relations suivantes des résistances du réseau en étoile en termes de résistances du réseau delta.
$$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$$
$$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$$
$$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$$
Remplacez les valeurs de R 1 , R 2 et R 3 dans les équations ci-dessus.
$$R_A = \frac{10 \times 60}{10 +60+30} = \frac{600}{100} = 6\Omega$$
$$R_B = \frac{60 \times 30}{10 +60+30} = \frac{1800}{100} = 18\Omega$$
$$R_C = \frac{30 \times 10}{10 +60+30} = \frac{300}{100} = 3\Omega$$
Donc, nous avons les résistances du réseau d'étoiles comme RA = 6 Ω, RB = 18 Ω et RC = 3 Ω, qui sont équivalentes aux résistances du réseau delta donné.
Dans le chapitre précédent, nous avons discuté de la conversion d'un réseau delta en un réseau en étoile équivalent. Parlons maintenant de la conversion du réseau en étoile en un réseau delta équivalent. Cette conversion est appeléeStar to Delta Conversion.
Dans le chapitre précédent, nous avons obtenu le resistances of star network du réseau delta comme
$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$ Equation 1
$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$ Equation 2
$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$ Equation 3
Résistances du réseau Delta en termes de résistances du réseau en étoile
Manipulons les équations ci-dessus afin d'obtenir les résistances du réseau delta en termes de résistances du réseau en étoile.
Multiply chaque ensemble de deux équations, puis add.
$$R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2^2 R_3 + R_2 R_3^2 R_1 + R_3 R_1^2 R_2}{(R_1 + R_2 + R_3)^2}$$
$$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3(R_1 + R_2 + R_3)}{(R_1 + R_2 + R_3)^2}$$
$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3}{R_1 + R_2 + R_3}$ Equation 4
En divisant l'équation 4 par l'équation 2, nous obtiendrons
$$\frac{R_A R_B + R_B R_C + R_C R_A}{R_B} = R_1$$
$$\Rightarrow R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$
En divisant l'équation 4 par l'équation 3, nous obtiendrons
$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$
En divisant l'équation 4 par l'équation 1, nous obtiendrons
$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$
En utilisant les relations ci-dessus, nous pouvons trouver les résistances du réseau delta à partir des résistances du réseau en étoile. De cette façon, nous pouvons convertirstar network into delta network.
Exemple
Calculons le resistances of delta network, qui sont équivalents à celui du réseau en étoile comme indiqué dans la figure suivante.
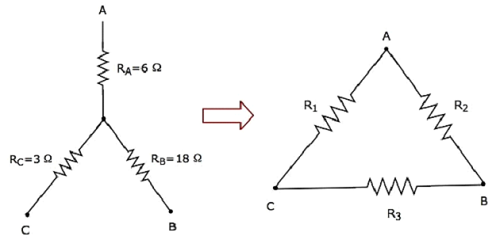
Compte tenu du resistances of star networkcomme R A = 6 Ω, R B = 18 Ω et R C = 3 Ω .
Nous connaissons les relations suivantes du resistances of delta network en termes de résistances de réseau en étoile.
$$R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$
$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$
$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$
Remplacez les valeurs de R A , R B et R C dans les équations ci-dessus.
$$R_1 = 3 + 6 + \frac{3 \times 6}{18} = 9 + 1 = 10 \Omega$$
$$R_2 = 6 + 18 + \frac{6 \times 18}{3} = 24 + 36 = 60 \Omega$$
$$R_3 = 18 + 3 + \frac{18 \times 3}{6} = 21 + 9 = 30 \Omega$$
Donc, nous avons les résistances du réseau delta comme R1 = 10 Ω, R2 = 60 Ω et R3 = 30 Ω, qui sont équivalentes aux résistances du réseau en étoile donné.
La topologie du réseau est une représentation graphique des circuits électriques. Il est utile pour analyser des circuits électriques complexes en les convertissant en graphiques de réseau. La topologie du réseau est également appeléeGraph theory.
Terminologie de base de la topologie de réseau
Maintenant, laissez-nous discuter de la terminologie de base impliquée dans cette topologie de réseau.
Graphique
Le graphe de réseau est simplement appelé graph. Il se compose d'un ensemble de nœuds connectés par des branches. Dans les graphiques, un nœud est un point commun à deux branches ou plus. Parfois, une seule branche peut se connecter au nœud. Une branche est un segment de ligne qui relie deux nœuds.
Tout circuit électrique ou réseau peut être converti en son équivalent graphen remplaçant les éléments passifs et les sources de tension par des courts-circuits et les sources de courant par des circuits ouverts. Cela signifie que les segments de ligne dans le graphique représentent les branches correspondant aux éléments passifs ou aux sources de tension du circuit électrique.
Exemple
Considérons ce qui suit electric circuit.
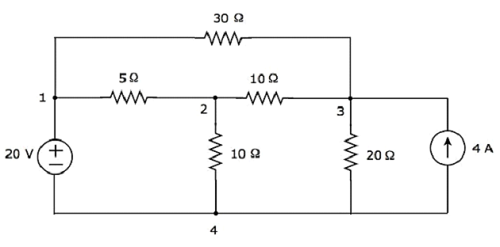
Dans le circuit ci-dessus, il y a four principal nodes et ceux-ci sont étiquetés avec 1, 2, 3 et 4. Il y a seven branches dans le circuit ci-dessus, parmi lesquels une branche contient une source de tension 20 V, une autre branche contient une source de courant 4 A et les cinq branches restantes contiennent des résistances ayant des résistances de 30 Ω, 5 Ω, 10 Ω, 10 Ω et 20 Ω respectivement.
Un équivalent graph correspondant au circuit électrique ci-dessus est montré dans la figure suivante.
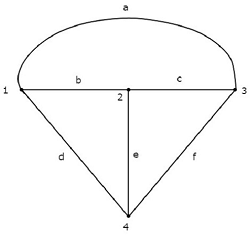
Dans le graphique ci-dessus, il y a four nodeset ceux sont étiquetés avec 1, 2, 3 et 4 respectivement. Ce sont les mêmes que ceux des nœuds principaux du circuit électrique. Il y asix branches dans le graphique ci-dessus et ceux sont étiquetés avec a, b, c, d, e et f respectivement.
Dans ce cas, nous avons one branch less dans le graphique car la source de courant 4 A est réalisée en circuit ouvert, tout en convertissant le circuit électrique en son graphique équivalent.
À partir de cet exemple, nous pouvons conclure les points suivants -
le number of nodes présent dans un graphe sera égal au nombre de nœuds principaux présents dans un circuit électrique.
le number of branches présent dans un graphe sera inférieur ou égal au nombre de branches présentes dans un circuit électrique.
Types de graphiques
Voici les types de graphiques -
- Graphique connecté
- Graphique non connecté
- Graphique dirigé
- Graphique non dirigé
Maintenant, parlons de ces graphiques un par un.
Graphique connecté
S'il existe au moins une branche entre l'un des deux nœuds d'un graphe, alors elle est appelée connected graph. Cela signifie que chaque nœud du graphe connecté aura une ou plusieurs branches qui lui sont connectées. Ainsi, aucun nœud ne se présentera comme isolé ou séparé.
Le graphique montré dans l'exemple précédent est un connected graph. Ici, tous les nœuds sont reliés par trois branches.
Graphique non connecté
S'il existe au moins un nœud dans le graphique qui reste non connecté par une seule branche, alors il est appelé comme un unconnected graph. Ainsi, il y aura un ou plusieurs nœuds isolés dans un graphe non connecté.
Considérez le graphique illustré dans la figure suivante.
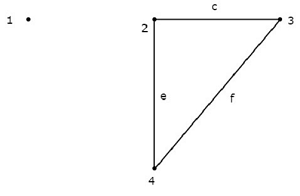
Dans ce graphe, les nœuds 2, 3 et 4 sont reliés par deux branches chacun. Mais, même pas une seule branche n'a été connectée aunode 1. Ainsi, le nœud 1 devient unisolated node. Par conséquent, le graphique ci-dessus est ununconnected graph.
Graphique dirigé
Si toutes les branches d'un graphe sont représentées par des flèches, alors ce graphe est appelé directed graph. Ces flèches indiquent le sens du courant dans chaque branche. Par conséquent, ce graphique est également appeléoriented graph.
Considérez le graphique illustré dans la figure suivante.
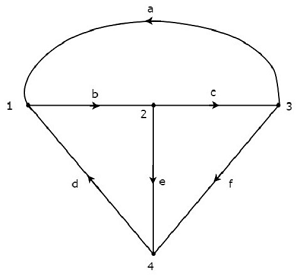
Dans le graphique ci-dessus, la direction du flux de courant est représentée par une flèche dans chaque branche. Par conséquent, c'est undirected graph.
Graphique non dirigé
Si les branches d'un graphe ne sont pas représentées par des flèches, alors ce graphe est appelé undirected graph. Puisqu'il n'y a pas de sens de circulation du courant, ce graphique est également appeléunoriented graph.
Le graphique qui a été montré dans le premier exemple de ce chapitre est un unoriented graph, car il n'y a pas de flèches sur les branches de ce graphique.
Sous-graphe et ses types
Une partie du graphique est appelée subgraph. Nous obtenons des sous-graphes en supprimant certains nœuds et / ou branches d'un graphe donné. Ainsi, le nombre de branches et / ou de nœuds d'un sous-graphe sera inférieur à celui du graphe d'origine. Par conséquent, nous pouvons conclure qu'un sous-graphe est un sous-ensemble d'un graphe.
Voici les two types des sous-graphiques.
- Tree
- Co-Tree
Arbre
Tree est un sous-graphe connecté d'un graphe donné, qui contient tous les nœuds d'un graphe. Mais, il ne devrait y avoir aucune boucle dans ce sous-graphe. Les branches d'un arbre sont appelées commetwigs.
Considérer ce qui suit connected subgraph du graphe, qui est montré dans l'exemple du début de ce chapitre.
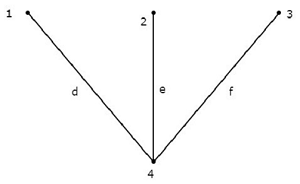
Ce sous-graphe connecté contient les quatre nœuds du graphe donné et il n'y a pas de boucle. Par conséquent, c'est unTree.
Cet arbre n'a que trois branches sur six branches d'un graphe donné. Parce que, si nous considérons ne serait-ce qu'une seule branche des branches restantes du graphe, alors il y aura une boucle dans le sous-graphe connecté ci-dessus. Ensuite, le sous-graphe connecté résultant ne sera pas un arbre.
De l'arbre ci-dessus, nous pouvons conclure que le number of branches qui sont présents dans un arbre doit être égal à n - 1 où 'n' est le nombre de nœuds du graphe donné.
Co-arbre
Co-Tree est un sous-graphe, qui est formé avec les branches qui sont supprimées tout en formant un arbre. Par conséquent, il est appelé commeComplementd'un arbre. Pour chaque arbre, il y aura un co-arbre correspondant et ses branches sont appelées commelinksou des accords. En général, les liens sont représentés par des lignes pointillées.
le Co-Tree correspondant à l'arbre ci-dessus est illustré dans la figure suivante.
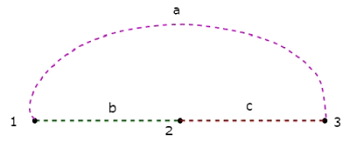
Ce Co-Tree n'a que trois nœuds au lieu de quatre nœuds du graphe donné, car le Node 4 est isolé du Co-Tree ci-dessus. Par conséquent, le Co-Tree n'a pas besoin d'être un sous-graphe connecté. Ce Co-Tree a trois branches et elles forment une boucle.
le number of branchesqui sont présents dans un co-arbre sera égal à la différence entre le nombre de branches d'un graphe donné et le nombre de brindilles. Mathématiquement, il peut être écrit comme
$$l = b - (n - 1)$$
$$l = b - n + 1$$
Où,
- l est le nombre de liens.
- b est le nombre de branches présentes dans un graphe donné.
- n est le nombre de nœuds présents dans un graphe donné.
Si nous combinons un arbre et son co-arbre correspondant, alors nous obtiendrons le original graph comme indiqué ci-dessous.
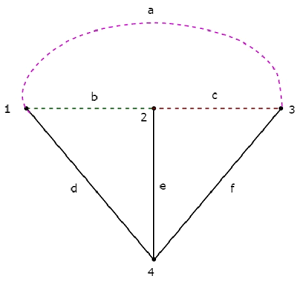
Les branches d'arbre d, e et f sont représentées par des lignes pleines. Les branches Co-Tree a, b et c sont représentées par des lignes pointillées.
Dans le chapitre précédent, nous avons expliqué comment convertir un circuit électrique en un graphe équivalent. Maintenant, parlons des matrices de topologie de réseau qui sont utiles pour résoudre tout problème de circuit électrique ou de réseau en utilisant leurs graphes équivalents.
Matrices associées aux graphes de réseau
Voici les trois matrices utilisées dans la théorie des graphes.
- Matrice d'incidence
- Matrice de boucle fondamentale
- Matrice de jeu de coupe fondamentale
Matrice d'incidence
Une matrice d'incidence représente le graphique d'un circuit électrique ou d'un réseau donné. Par conséquent, il est possible de dessiner le graphique de ce même circuit électrique ou réseau à partir duincidence matrix.
Nous savons que le graphe est constitué d'un ensemble de nœuds et que ceux-ci sont reliés par quelques branches. Ainsi, la connexion des branches à un nœud est appelée incidence. La matrice d'incidence est représentée par la lettre A. Elle est également appelée matrice d'incidence de nœud à branche ounode incidence matrix.
S'il y a 'n' nœuds et 'b' branches sont présentes dans un directed graph, alors la matrice d'incidence aura «n» lignes et «b» colonnes. Ici, les lignes et les colonnes correspondent aux nœuds et aux branches d'un graphe orienté. D'où leorder de la matrice d'incidence sera n × b.
le elements of incidence matrix aura l'une de ces trois valeurs, +1, -1 et 0.
Si le courant de branche part d'un nœud sélectionné, la valeur de l'élément sera +1.
Si le courant de branche entre vers un nœud sélectionné, alors la valeur de l'élément sera -1.
Si le courant de branche n'entre pas à un nœud sélectionné ni ne sort d'un nœud sélectionné, alors la valeur de l'élément sera 0.
Procédure pour trouver la matrice d'incidence
Suivez ces étapes afin de trouver la matrice d'incidence du graphe orienté.
Sélectionnez un nœud à un instant du graphe orienté donné et remplissez les valeurs des éléments de la matrice d'incidence correspondant à ce nœud dans une ligne.
Répétez l'étape ci-dessus pour tous les nœuds du graphe orienté donné.
Exemple
Considérer ce qui suit directed graph.

le incidence matrix correspondant au graphique dirigé ci-dessus sera
$$A = \begin{bmatrix}-1 & 1 & 0 & -1 & 0 & 0\\0 & -1 & 1 & 0 & 1 & 0\\1 & 0 & -1 & 0 & 0 & 1 \\0 & 0 & 0 & 1 & -1 & -1 \end{bmatrix}$$
Les lignes et les colonnes de la matrice ci-dessus représentent les nœuds et les branches d'un graphe orienté donné. L'ordre de cette matrice d'incidence est 4 × 6.
En observant la matrice d'incidence ci-dessus, nous pouvons conclure que le summationdes éléments de colonne de la matrice d'incidence est égal à zéro. Cela signifie qu'un courant de branche part d'un nœud et entre à un autre nœud unique uniquement.
Note- Si le graphe donné est de type non dirigé, convertissez-le en graphe orienté en représentant les flèches sur chaque branche de celui-ci. Nous pouvons considérer la direction arbitraire du flux de courant dans chaque branche.
Matrice de boucle fondamentale
Boucle fondamentale ou f-loopest une boucle, qui ne contient qu'un seul lien et une ou plusieurs brindilles. Ainsi, le nombre de f-loops sera égal au nombre de liens. La matrice de boucle fondamentale est représentée par la lettre B. Elle est également appeléefundamental circuit matrixet matrice de jeu de liens. Cette matrice donne la relation entre les courants de branche et les courants de liaison.
S'il y a 'n' nœuds et 'b' branches sont présentes dans un directed graph, alors le nombre de liens présents dans un co-arbre, qui correspond à l'arbre sélectionné du graphe donné sera b-n + 1.
Ainsi, la matrice de boucle fondamentale aura des lignes «b-n + 1» et des colonnes «b». Ici, les lignes et les colonnes correspondent aux liens du co-arbre et des branches d'un graphe donné. Par conséquent, l'ordre de la matrice de boucle fondamentale sera(b - n + 1) × b.
le elements of fundamental loop matrix aura l'une de ces trois valeurs, +1, -1 et 0.
La valeur de l'élément sera +1 pour le lien de la boucle f sélectionnée.
La valeur des éléments sera 0 pour les liens et brindilles restants, qui ne font pas partie de la f-loop sélectionnée.
Si la direction du courant de brindille de la boucle f sélectionnée est la même que celle du courant de liaison de la boucle f, alors la valeur de l'élément sera +1.
Si la direction du courant de brindille de la boucle f sélectionnée est opposée à celle du courant de liaison de la boucle f, alors la valeur de l'élément sera -1.
Procédure pour trouver la matrice de boucle fondamentale
Suivez ces étapes afin de trouver la matrice de boucle fondamentale d'un graphe orienté donné.
Sélectionnez un arbre de graphe orienté donné.
En incluant un lien à la fois, nous obtiendrons une f-loop. Remplissez les valeurs des éléments correspondant à cette f-boucle dans une ligne de matrice de boucle fondamentale.
Répétez l'étape ci-dessus pour tous les liens.
Exemple
Jetez un œil à l'Arbre de directed graph, qui est considérée pour la matrice d'incidence.

L'arbre ci-dessus contient trois branches d, e et f. Par conséquent, les branches a, b et c seront les liens du Co-Tree correspondant à l'arbre ci-dessus. En incluant un lien à la fois vers l'arbre ci-dessus, nous en obtiendrons unf-loop. Donc, il y en aura troisf-loops, car il existe trois liens. Ces trois boucles f sont illustrées dans la figure suivante.
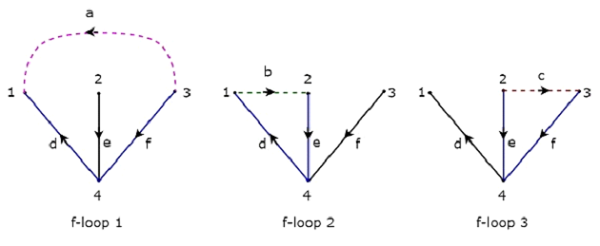
Dans la figure ci-dessus, les branches, qui sont représentées avec des lignes colorées forment des f-boucles. Nous obtiendrons les valeurs d'élément ligne par ligne de la matrice Tie-set à partir de chaque f-loop. Alors leTieset matrix de l'arbre considéré ci-dessus sera
$$B = \begin{bmatrix}1 & 0 & 0 & -1 & 0 & -1\\0 & 1 & 0 & 1 & 1 & 0\\0 & 0 & 1 & 0 & -1 & 1 \end{bmatrix}$$
Les lignes et colonnes de la matrice ci-dessus représentent les liens et les branches d'un graphe orienté donné. L'ordre de cette matrice d'incidence est 3 × 6.
le number of Fundamental loop matricesd'un graphe orienté sera égal au nombre d'arbres de ce graphe orienté. Parce que chaque arbre aura une matrice de boucle fondamentale.
Matrice de coupe fondamentale
Ensemble de coupe fondamentale ou f-cut setest le nombre minimum de branches qui sont supprimées d'un graphe de telle sorte que le graphe original devienne deux sous-graphes isolés. L'ensemble f-cut contient uniquementone twiget un ou plusieurs liens. Ainsi, le nombre d'ensembles f-cut sera égal au nombre de brindilles.
Fundamental cut set matrix est représenté par la lettre C. Cette matrice donne la relation entre les tensions de branche et les tensions de brindille.
S'il y a 'n' nœuds et 'b' branches sont présentes dans un directed graph, alors le nombre de brindilles présentes dans un arbre sélectionné d'un graphe donné sera n-1. Ainsi, la matrice d'ensemble de coupes fondamentales aura «n-1» lignes et «b» colonnes. Ici, les lignes et les colonnes correspondent aux brindilles de l'arbre sélectionné et aux branches du graphique donné. D'où leorder de la matrice d'ensemble de coupes fondamentales sera (n-1) × b.
le elements of fundamental cut set matrix aura l'une de ces trois valeurs, +1, -1 et 0.
La valeur de l'élément sera +1 pour la brindille du f-cutset sélectionné.
La valeur des éléments sera 0 pour les brindilles et liens restants, qui ne font pas partie du f-cutset sélectionné.
Si la direction du courant de liaison de l'ensemble f-cut sélectionné est la même que celle du courant de brindille f-cutset, alors la valeur de l'élément sera +1.
Si la direction du courant de liaison de l'ensemble f-cut sélectionné est opposée à celle du courant de brindille f-cutset, alors la valeur de l'élément sera -1.
Procédure pour trouver la matrice de coupe fondamentale
Suivez ces étapes afin de trouver la matrice d'ensemble de coupes fondamentale d'un graphe orienté donné.
Sélectionnez un arbre de graphe orienté donné et représentez les liens avec les lignes pointillées.
En supprimant une brindille et les liens nécessaires à la fois, nous obtiendrons un ensemble f-cut. Remplissez les valeurs des éléments correspondant à cet ensemble de coupes f dans une rangée de matrice d'ensemble de coupes fondamentales.
Répétez l'étape ci-dessus pour toutes les brindilles.
Exemple
Considérez la même chose directed graph , dont nous avons discuté dans la section de la matrice d'incidence. Sélectionnez les branches d, e et f de ce graphe orienté sous forme de brindilles. Ainsi, les branches restantes a, b et c de ce graphe orienté seront les liens.
le twigs d, e et f sont représentés par des lignes pleines et links a, b et c sont représentés par des lignes pointillées dans la figure suivante.
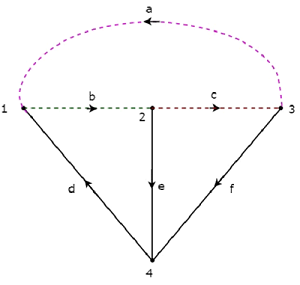
En supprimant une brindille et les liens nécessaires à la fois, nous obtiendrons un ensemble f-cut. Donc, il y aura trois ensembles f-cut, puisqu'il y a trois brindilles. Ces troisf-cut sets sont illustrés dans la figure suivante.

Nous aurons trois ensembles f-cut en supprimant un ensemble de brindilles et de liens de C 1 , C 2 et C 3 . Nous obtiendrons les valeurs d'élément par ligne de la matrice d'ensemble de coupes fondamentales à partir de chaque ensemble de coupes f. Alors lefundamental cut set matrix de l'arbre considéré ci-dessus sera
$$C = \begin{bmatrix}1 & -1 & 0 & 1 & 0 & 0\\0 & -1 & 1 & 0 & 1 & 0\\1 & 0 & -1 & 0 & 0 & 1 \end{bmatrix}$$
Les lignes et colonnes de la matrice ci-dessus représentent les brindilles et les branches d'un graphe orienté donné. L'ordre de cette matrice d'ensemble de coupes fondamentales est 3 × 6.
le number of Fundamental cut set matricesd'un graphe orienté sera égal au nombre d'arbres de ce graphe orienté. Parce que chaque arbre aura une matrice d'ensemble de coupe fondamentale.
Superposition theoremest basé sur le concept de linéarité entre la réponse et l'excitation d'un circuit électrique. Il déclare que la réponse dans une branche particulière d'un circuit linéaire lorsque plusieurs sources indépendantes agissent en même temps est équivalente à la somme des réponses dues à chaque source indépendante agissant à la fois.
Dans cette méthode, nous ne considérerons que one independent sourceà la fois. Nous devons donc éliminer les sources indépendantes restantes du circuit. On peut éliminer les sources de tension en court-circuitant leurs deux bornes et de même, les sources de courant en ouvrant leurs deux bornes.
Par conséquent, nous devons trouver la réponse dans une branche particulière ‘n’ timess'il y a 'n' sources indépendantes. La réponse dans une branche particulière pourrait être soit un courant circulant dans cette branche, soit une tension à travers cette branche.
Procédure du théorème de superposition
Suivez ces étapes afin de trouver la réponse dans une branche particulière en utilisant le théorème de superposition.
Step 1 - Trouvez la réponse dans une branche particulière en considérant une source indépendante et en éliminant les sources indépendantes restantes présentes dans le réseau.
Step 2 - Répétez l'étape 1 pour toutes les sources indépendantes présentes sur le réseau.
Step 3 - Ajouter toutes les réponses afin d'obtenir la réponse globale dans une branche particulière lorsque toutes les sources indépendantes sont présentes dans le réseau.
Exemple
Trouvez le courant traversant la résistance de 20 Ω du circuit suivant en utilisant superposition theorem.
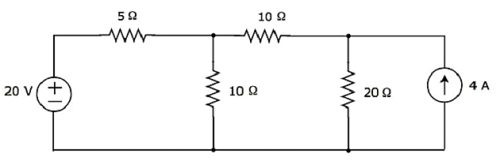
Step 1 - Trouvons le courant traversant la résistance de 20 Ω en considérant uniquement 20 V voltage source. Dans ce cas, on peut éliminer la source de courant 4 A en en faisant un circuit ouvert. Le schéma de circuit modifié est illustré dans la figure suivante.

Il n'y a qu'un seul nœud principal sauf Ground dans le circuit ci-dessus. Donc, nous pouvons utilisernodal analysisméthode. La tension de nœud V 1 est indiquée dans la figure suivante. Ici, V 1 est la tension du nœud 1 par rapport à la masse.
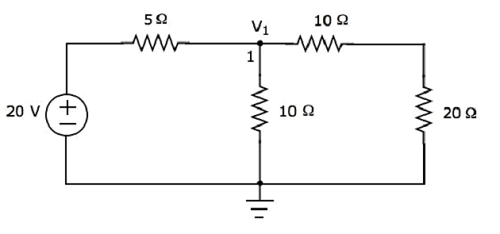
le nodal equation au nœud 1 est
$$\frac{V_1 - 20}{5} + \frac{V_1}{10} + \frac{V_1}{10 + 20} = 0$$
$$\Rightarrow \frac{6V_1 - 120 + 3V_1 + V_1}{30} = 0$$
$$\Rightarrow 10V_1 = 120$$
$$\Rightarrow V_1 = 12V$$
le current flowing through 20 Ω resistor peut être trouvée en faisant la simplification suivante.
$$I_1 = \frac{V_1}{10 + 20}$$
Remplacez la valeur de V 1 dans l'équation ci-dessus.
$$I_1 = \frac{12}{10 + 20} = \frac{12}{30} = 0.4 A$$
Par conséquent, le courant traversant la résistance de 20 Ω est 0.4 A, lorsque seule une source de tension de 20 V est prise en compte.
Step 2 - Trouvons le courant traversant la résistance de 20 Ω en considérant uniquement 4 A current source. Dans ce cas, on peut éliminer la source de tension 20 V en la faisant en court-circuit. Le schéma de circuit modifié est illustré dans la figure suivante.
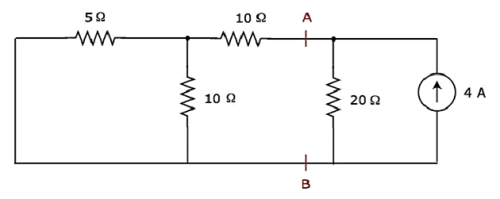
Dans le circuit ci-dessus, il y a trois résistances à gauche des bornes A et B.Nous pouvons remplacer ces résistances par une seule equivalent resistor. Ici, les résistances 5 Ω et 10 Ω sont connectées en parallèle et toute la combinaison est en série avec une résistance de 10 Ω.
le equivalent resistance à gauche des terminaux A et B sera
$$R_{AB} = \lgroup \frac{5 \times 10}{5 + 10} \rgroup + 10 = \frac{10}{3} + 10 = \frac{40}{3} \Omega$$
Le schéma de circuit simplifié est illustré dans la figure suivante.
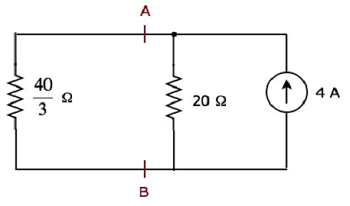
Nous pouvons trouver le courant traversant la résistance de 20 Ω, en utilisant current division principle.
$$I_2 = I_S \lgroup \frac{R_1}{R_1 + R_2} \rgroup$$
Remplacer $I_S = 4A,\: R_1 = \frac{40}{3} \Omega$ et $R_2 = 20 \Omega$ dans l'équation ci-dessus.
$$I_2 = 4 \lgroup \frac{\frac{40}{3}}{\frac{40}{3} + 20} \rgroup = 4 \lgroup \frac{40}{100} \rgroup = 1.6 A$$
Par conséquent, le courant traversant la résistance de 20 Ω est 1.6 A, lorsque seulement une source de courant de 4 A est prise en compte.
Step 3 - Nous obtiendrons le courant traversant la résistance de 20 Ω du circuit donné en faisant le addition of two currents que nous avons obtenu aux étapes 1 et 2. Mathématiquement, il peut s'écrire
$$I = I_1 + I_2$$
Remplacez par les valeurs de I 1 et I 2 dans l'équation ci-dessus.
$$I = 0.4 + 1.6 = 2 A$$
Par conséquent, le courant traversant la résistance de 20 Ω d'un circuit donné est 2 A.
Note - On ne peut pas appliquer directement le théorème de superposition pour trouver la quantité de powerlivré à toute résistance présente dans un circuit linéaire, simplement en ajoutant les puissances délivrées à cette résistance en raison de chaque source indépendante. Au contraire, nous pouvons calculer soit le courant total traversant ou la tension à travers cette résistance en utilisant le théorème de superposition et à partir de cela, nous pouvons calculer la quantité de puissance fournie à cette résistance en utilisant$I^2 R$ ou $\frac{V^2}{R}$.
Thevenin’s theoremindique que tout réseau ou circuit linéaire à deux bornes peut être représenté avec un réseau ou un circuit équivalent, qui consiste en une source de tension en série avec une résistance. Il est connu comme le circuit équivalent de Thevenin. Un circuit linéaire peut contenir des sources indépendantes, des sources dépendantes et des résistances.
Si le circuit contient plusieurs sources indépendantes, des sources dépendantes et des résistances, la réponse dans un élément peut être facilement trouvée en remplaçant l'ensemble du réseau à gauche de cet élément par un Thevenin’s equivalent circuit.
le response in an element peut être la tension à travers cet élément, le courant traversant cet élément ou la puissance dissipée à travers cet élément.
Ce concept est illustré dans les figures suivantes.
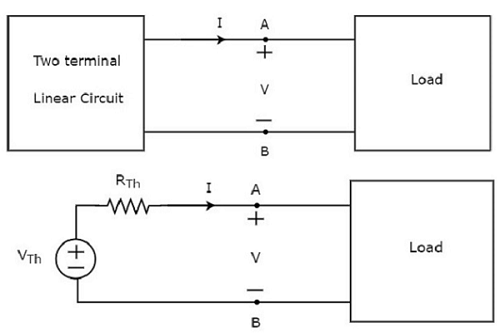
Thevenin’s equivalent circuitressemble à une source de tension pratique. Par conséquent, il a une source de tension en série avec une résistance.
La source de tension présente dans le circuit équivalent de Thevenin est appelée tension équivalente de Thevenin ou simplement Thevenin’s voltage, VTh.
La résistance présente dans le circuit équivalent de Thevenin est appelée résistance équivalente de Thevenin ou simplement Thevenin’s resistor, RTh.
Méthodes de recherche du circuit équivalent de Thevenin
Il existe trois méthodes pour trouver un circuit équivalent de Thevenin. Basé surtype of sourcesprésentes dans le réseau, nous pouvons choisir l'une de ces trois méthodes. Maintenant, laissez-nous discuter de deux méthodes une par une. Nous discuterons de la troisième méthode dans le chapitre suivant.
Méthode 1
Suivez ces étapes pour trouver le circuit équivalent du Thevenin, lorsque seul le sources of independent type sont présents.
Step 1 - Considérez le schéma électrique en ouvrant les bornes par rapport auxquelles se trouve le circuit équivalent de Thevenin.
Step 2 - Trouvez la tension de Thevenin VTh aux bornes ouvertes du circuit ci-dessus.
Step 3 - Trouvez la résistance de Thevenin RTh aux bornes ouvertes du circuit ci-dessus en éliminant les sources indépendantes qui y sont présentes.
Step 4 - Dessinez le Thevenin’s equivalent circuiten connectant une tension de Thevenin V Th en série avec une résistance de Thevenin R Th .
Maintenant, nous pouvons trouver la réponse dans un élément qui se trouve sur le côté droit du circuit équivalent de Thevenin.
Exemple
Trouvez le courant traversant la résistance de 20 Ω en trouvant d'abord un Thevenin’s equivalent circuit à gauche des bornes A et B.
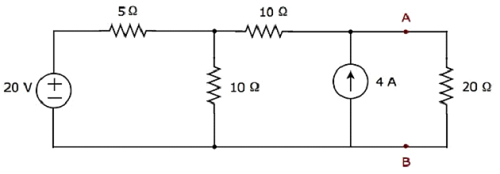
Step 1 - Afin de trouver le circuit équivalent de Thevenin sur le côté gauche des bornes A et B, nous devons retirer la résistance de 20 Ω du réseau en opening the terminals A & B. Le schéma de circuit modifié est illustré dans la figure suivante.
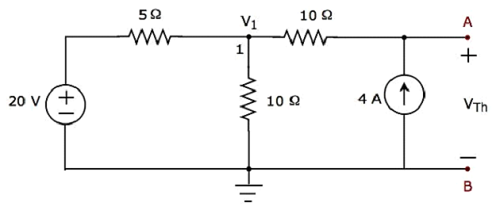
Step 2 - Calcul de Thevenin’s voltage VTh.
Il n'y a qu'un seul nœud principal sauf Ground dans le circuit ci-dessus. Donc, nous pouvons utilisernodal analysisméthode. La tension de nœud V 1 et la tension de Thevenin V Th sont indiquées dans la figure ci-dessus. Ici, V 1 est la tension du nœud 1 par rapport à la masse et V Th est la tension aux bornes de la source de courant 4 A.
le nodal equation au nœud 1 est
$$\frac{V_1 - 20}{5} + \frac{V_1}{10} - 4 = 0$$
$$\Rightarrow \frac{2V_1 - 40 + V_1 - 40}{10} = 0$$
$$\Rightarrow 3V_1 - 80 = 0$$
$$\Rightarrow V_1 = \frac{80}{3}V$$
La tension aux bornes de la résistance de la branche série 10 Ω est
$$V_{10 \Omega} = (-4)(10) = -40V$$
Il y a deux mailles dans le circuit ci-dessus. leKVL equation autour du deuxième maillage est
$$V_1 - V_{10 \Omega} - V_{Th} = 0$$
Remplacez les valeurs de $V_1$ et $V_{10 \Omega}$ dans l'équation ci-dessus.
$$\frac{80}{3} - (-40) - V_{Th} = 0$$
$$V_{Th} = \frac{80 + 120}{3} = \frac{200}{3}V$$
Par conséquent, la tension du Thevenin est $V_{Th} = \frac{200}{3}V$
Step 3 - Calcul de Thevenin’s resistance RTh.
Court-circuitez la source de tension et ouvrez la source de courant du circuit ci-dessus afin de calculer la résistance de Thevenin R Th aux bornes A et B.modified circuit diagram est illustré dans la figure suivante.
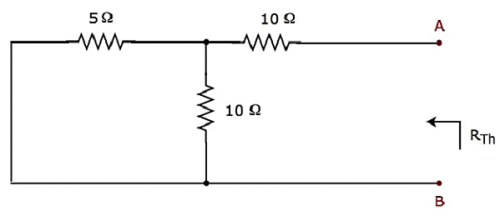
La résistance de Thevenin entre les bornes A et B sera
$$R_{Th} = \lgroup \frac{5 \times 10}{5 + 10} \rgroup + 10 = \frac{10}{3} + 10 = \frac{40}{3} \Omega$$
Par conséquent, la résistance de Thevenin est $\mathbf {R_{Th} = \frac{40}{3} \Omega}$.
Step 4- Le circuit équivalent de Thevenin est placé à gauche des bornes A et B dans le circuit donné. Ce schéma de circuit est illustré dans la figure suivante.

Le courant traversant la résistance de 20 Ω peut être trouvé en substituant les valeurs de V Th , R Th et R dans l'équation suivante.
$$l = \frac{V_{Th}}{R_{Th} + R}$$
$$l = \frac{\frac{200}{3}}{\frac{40}{3} + 20} = \frac{200}{100} = 2A$$
Par conséquent, le courant traversant la résistance de 20 Ω est 2 A.
Méthode 2
Suivez ces étapes afin de trouver le circuit équivalent du Thevenin, lorsque le sources of both independent type and dependent type sont présents.
Step 1 - Considérez le schéma électrique en ouvrant les bornes par rapport auxquelles se trouve le circuit équivalent de Thevenin.
Step 2 - Trouvez la tension de Thevenin VTh aux bornes ouvertes du circuit ci-dessus.
Step 3 - Trouver le courant de court-circuit ISC en court-circuitant les deux bornes ouvertes du circuit ci-dessus.
Step 4 - Trouvez la résistance de Thevenin RTh en utilisant la formule suivante.
$$R_{Th} = \frac{V_{Th}}{I_{SC}}$$
Step 5 - Dessinez le Thevenin’s equivalent circuiten connectant une tension de Thevenin V Th en série avec une résistance de Thevenin R Th .
Maintenant, nous pouvons trouver la réponse dans un élément qui se trouve sur le côté droit du circuit équivalent de Thevenin.
Norton’s theoremest similaire au théorème de Thevenin. Il indique que tout réseau ou circuit linéaire à deux terminaux peut être représenté avec un réseau ou un circuit équivalent, qui consiste en une source de courant en parallèle avec une résistance. Il est connu commeNorton’s equivalent circuit. Un circuit linéaire peut contenir des sources indépendantes, des sources dépendantes et des résistances.
Si un circuit a plusieurs sources indépendantes, sources dépendantes et résistances, la réponse dans un élément peut être facilement trouvée en remplaçant l'ensemble du réseau à gauche de cet élément par un Norton’s equivalent circuit.
le response in an element peut être la tension à travers cet élément, le courant circulant à travers cet élément ou la puissance dissipée à travers cet élément.
Ce concept est illustré dans les figures suivantes.
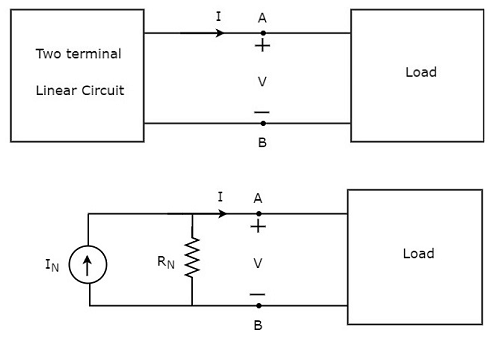
Norton’s equivalent circuitressemble à une source de courant pratique. Par conséquent, il a une source de courant en parallèle avec une résistance.
La source de courant présente dans le circuit équivalent de Norton est appelée courant équivalent de Norton ou simplement Norton’s current IN.
La résistance présente dans le circuit équivalent de Norton est appelée résistance équivalente de Norton ou simplement Norton’s resistor RN.
Méthodes de recherche du circuit équivalent de Norton
Il y a three methodspour trouver le circuit équivalent d'un Norton. En fonction du type de sources présentes dans le réseau, nous pouvons choisir l'une de ces trois méthodes. Maintenant, laissez-nous discuter de ces trois méthodes une par une.
Méthode 1
Suivez ces étapes afin de trouver le circuit équivalent de Norton, lorsque seul le sources of independent type sont présents.
Step 1 - Considérez le schéma électrique en ouvrant les bornes par rapport auxquelles se trouve le circuit équivalent du Norton.
Step 2 - Trouvez le courant de Norton IN en court-circuitant les deux bornes ouvertes du circuit ci-dessus.
Step 3 - Trouvez la résistance de Norton RNaux bornes ouvertes du circuit considéré à l'étape 1 en éliminant les sources indépendantes qui y sont présentes. La résistance de NortonRN sera la même que celle de la résistance de Thevenin RTh.
Step 4 - Dessinez le Norton’s equivalent circuiten connectant le courant IN d'un Norton en parallèle avec la résistance R N de Norton .
Maintenant, nous pouvons trouver la réponse dans un élément qui se trouve sur le côté droit du circuit équivalent de Norton.
Méthode 2
Suivez ces étapes afin de trouver le circuit équivalent de Norton, lorsque le sources of both independent type and dependent type sont présents.
Step 1 - Considérez le schéma de circuit en ouvrant les bornes par rapport auxquelles se trouve le circuit équivalent de Norton.
Step 2 - Trouvez la tension en circuit ouvert VOC aux bornes ouvertes du circuit ci-dessus.
Step 3 - Trouvez le courant de Norton IN en court-circuitant les deux bornes ouvertes du circuit ci-dessus.
Step 4 - Trouvez la résistance de Norton RN en utilisant la formule suivante.
$$R_N = \frac{V_{OC}}{I_N}$$
Step 5- Dessinez le circuit équivalent de Norton en connectant le courant I N d' un Norton en parallèle avec la résistance R N de Norton .
Maintenant, nous pouvons trouver la réponse dans un élément qui se trouve sur le côté droit du circuit équivalent de Norton.
Méthode 3
Il s'agit d'une méthode alternative pour trouver le circuit équivalent d'un Norton.
Step 1 - Trouver un Thevenin’s equivalent circuitentre les deux terminaux souhaités. Nous savons qu'il se compose d'une source de tension de Thevenin, V Th et d'une résistance de Thevenin, R Th .
Step 2 - Appliquer source transformation techniqueau circuit équivalent de Thevenin ci-dessus. Nous obtiendrons le circuit équivalent de Norton. Ici,
Le courant de Norton,
$$I_N = \frac{V_{Th}}{R_{Th}}$$
La résistance de Norton,
$$R_N = R_{Th}$$
Ce concept est illustré dans la figure suivante.
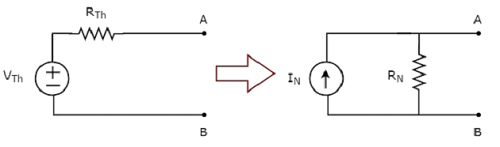
Maintenant, nous pouvons trouver la réponse dans un élément en plaçant le circuit équivalent de Norton à gauche de cet élément.
Note- De même, nous pouvons trouver le circuit équivalent de Thevenin en trouvant d'abord le circuit équivalent d'un Norton, puis en lui appliquant la technique de transformation de source. Ce concept est illustré dans la figure suivante.
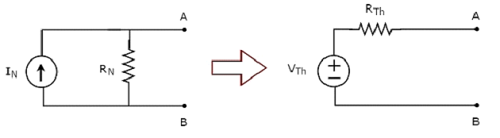
C'est la méthode 3 pour trouver un circuit équivalent de Thevenin.
Exemple
Trouvez le courant traversant la résistance de 20 Ω en trouvant d'abord un Norton’s equivalent circuit à gauche des bornes A et B.
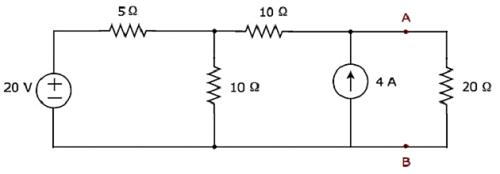
Résolvons ce problème en utilisant Method 3.
Step 1- Dans le chapitre précédent, nous avons calculé le circuit équivalent de Thevenin sur le côté gauche des bornes A et B. Nous pouvons utiliser ce circuit maintenant. Il est illustré dans la figure suivante.
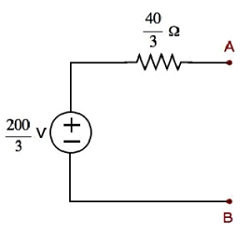
Ici, la tension de Thevenin, $V_{Th} = \frac{200}{3} V$ et la résistance de Thevenin, $R_{Th} = \frac{40}{3} \Omega$
Step 2 - Appliquer source transformation techniqueau circuit équivalent de Thevenin ci-dessus. Remplacez les valeurs de V Th et R Th dans la formule suivante deNorton’s current.
$$I_N = \frac{V_{Th}}{R_{Th}}$$
$$I_N = \frac{\frac{200}{3}}{\frac{40}{3}} = 5A$$
Par conséquent, le I N actuel de Norton est5 A.
On sait que la résistance de Norton, R N est la même que celle de la résistance de Thevenin R Th .
$$\mathbf {R_N = \frac{40}{3} \Omega}$$
Le circuit équivalent de Norton correspondant au circuit équivalent de Thevenin ci-dessus est illustré dans la figure suivante.
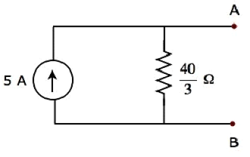
Maintenant, placez le circuit équivalent du Norton à gauche des bornes A et B du circuit donné.
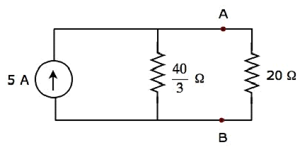
En utilisant current division principle, le courant traversant la résistance de 20 Ω sera
$$I_{20 \Omega} = 5 \lgroup \frac{\frac{40}{3}}{\frac{40}{3} + 20} \rgroup$$
$$I_{20 \Omega} = 5 \lgroup \frac{40}{100} \rgroup = 2A$$
Par conséquent, le courant traversant la résistance de 20 Ω est 2 A.
La quantité d'énergie reçue par une charge est un paramètre important dans les applications électriques et électroniques. Dans les circuits CC, nous pouvons représenter la charge avec une résistance ayant une résistance de R L ohms. De même, dans les circuits alternatifs, nous pouvons le représenter avec une charge complexe ayant une impédance de Z L ohms.
Maximum power transfer theorem indique que la source de tension CC fournira une puissance maximale à la résistance de charge variable uniquement lorsque la résistance de charge est égale à la résistance de la source.
De même, Maximum power transfer theorem indique que la source de tension alternative fournira une puissance maximale à la charge complexe variable uniquement lorsque l'impédance de charge est égale au conjugué complexe de l'impédance de la source.
Dans ce chapitre, discutons du théorème de transfert de puissance maximum pour les circuits CC.
Preuve du théorème de transfert de puissance maximale
Remplacez tout réseau linéaire à deux bornes ou circuit sur le côté gauche de la résistance de charge variable ayant une résistance de R L ohms par un circuit équivalent de Thevenin. Nous savons que le circuit équivalent de Thevenin ressemble à une source de tension pratique.
Ce concept est illustré dans les figures suivantes.
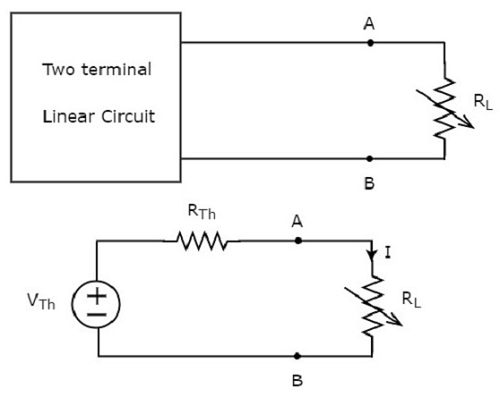
La quantité de puissance dissipée à travers la résistance de charge est
$$P_L = I^2 R_L$$
Remplacer $I = \frac{V_{Th}}{R_{Th} + R_L}$ dans l'équation ci-dessus.
$$P_L = \lgroup \frac{V_{Th}}{(R_{Th} + R_L)} \rgroup ^2 R_L$$
$\Rightarrow P_L = {V_{Th}}^2 \lbrace \frac{R_L}{(R_{Th} + R_L)^2} \rbrace$ Equation 1
Condition de transfert de puissance maximum
Pour un maximum ou un minimum, la première dérivée sera zéro. Donc, différenciez l'équation 1 par rapport à R L et rendez-la égale à zéro.
$$\frac{dP_L}{dR_L} = {V_{Th}}^2 \lbrace \frac{(R_{Th} + R_L)^2 \times 1 - R_L \times 2(R_{Th} + R_L)}{(R_{Th} + R_L)^4} \rbrace = 0$$
$$\Rightarrow (R_{Th} + R_L)^2 -2R_L(R_{Th} + R_L) = 0$$
$$\Rightarrow (R_{Th} + R_L)(R_{Th} + R_L - 2R_L) = 0$$
$$\Rightarrow (R_{Th} - R_L) = 0$$
$$\Rightarrow R_{Th} = R_L\:or\:R_L = R_{Th}$$
Par conséquent, la condition for maximum power la dissipation à travers la charge est $R_L = R_{Th}$. Cela signifie que si la valeur de la résistance de charge est égale à la valeur de la résistance de la source, c'est-à-dire la résistance de Thevenin, alors la puissance dissipée à travers la charge sera de valeur maximale.
La valeur du transfert de puissance maximal
Remplacer $R_L = R_{Th}\:\&\:P_L = P_{L, Max}$ dans l'équation 1.
$$P_{L, Max} = {V_{Th}}^2 \lbrace \frac{R_{Th}}{(R_{Th} + R_{Th})^2} \rbrace$$
$$P_{L, Max} = {V_{Th}}^2 \lbrace \frac{R_{Th}}{4 {R_{Th}}^2} \rbrace$$
$$\Rightarrow P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{Th}}$$
$$\Rightarrow P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{L}}, \: since \: R_{L} = R_{Th}$$
Par conséquent, la maximum amount of power transféré à la charge est
$$P_{L, Max} = \frac{{V_{Th}}^2}{4R_{L}} = \frac{{V_{Th}}^2}{4R_{Th}}$$
Efficacité du transfert de puissance maximal
Nous pouvons calculer l'efficacité du transfert de puissance maximal, $\eta_{Max}$ en utilisant la formule suivante.
$\eta_{Max} = \frac{P_{L, Max}}{P_S}$ Equation 2
Où,
$P_{L, Max}$ est la quantité maximale de puissance transférée à la charge.
$P_S$ est la quantité d'énergie produite par la source.
le amount of power generated par la source est
$$P_S = I^2 R_{Th} + I^2 R_L$$
$$\Rightarrow P_S = 2 I^2 R_{Th},\:since\:R_{L} = R_{Th}$$
Remplacer $I = \frac{V_{Th}}{2 R_{Th}}$ dans l'équation ci-dessus.
$$P_S = 2\lgroup \frac{V_{Th}}{2 R_{Th}} \rgroup ^2 R_{Th}$$
$$\Rightarrow P_S = 2\lgroup \frac{{V_{Th}}^2}{4 {R_{Th}}^2} \rgroup R_{Th}$$
$$\Rightarrow P_S = \frac{{V_{Th}}^2}{2 R_{Th}}$$
Remplacez les valeurs de $P_{L, Max}$ et $P_S$ dans l'équation 2.
$$\eta_{Max} = \frac{\lgroup \frac{{V_{Th}}^2}{4R_{Th}} \rgroup}{\lgroup \frac{{V_{Th}}^2}{2R_{Th}}\rgroup}$$
$$\Rightarrow \eta_{Max} = \frac{1}{2}$$
Nous pouvons représenter l'efficacité du transfert de puissance maximal en termes de percentage comme suit -
$$\% \eta_{Max} = \eta_{Max} \times 100\%$$
$$\Rightarrow \% \eta_{Max} = \lgroup \frac{1}{2} \rgroup \times 100\%$$
$$\Rightarrow \% \eta_{Max} = 50\%$$
Par conséquent, l'efficacité du transfert de puissance maximal est 50 %.
Exemple
Trouvez le maximum powerqui peut être fournie à la résistance de charge R L du circuit représenté sur la figure suivante.
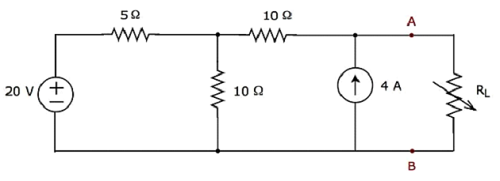
Step 1- Dans le chapitre Théorème de Thevenin, nous avons calculé le circuit équivalent de Thevenin sur le côté gauche des bornes A et B. Nous pouvons utiliser ce circuit maintenant. Il est illustré dans la figure suivante.
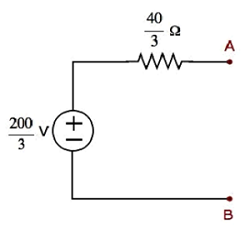
Ici, la tension de Thevenin $V_{Th} = \frac{200}{3}V$ et la résistance de Thevenin $R_{Th} = \frac{40}{3} \Omega$
Step 2- Remplacez la partie du circuit, qui est du côté gauche des bornes A et B du circuit donné par le circuit équivalent de Thevenin ci-dessus. Le schéma électrique résultant est illustré dans la figure suivante.

Step 3- On peut trouver la puissance maximale qui sera fournie à la résistance de charge, R L en utilisant la formule suivante.
$$P_{L, Max} = \frac{{V_{Th}}^2}{4 R_{Th}}$$
Remplacer $V_{Th} = \frac{200}{3}V$ et $R_{Th} = \frac{40}{3} \Omega$ dans la formule ci-dessus.
$$P_{L, Max} = \frac{\lgroup \frac{200}{3} \rgroup ^ 2}{4 \lgroup \frac{40}{3}\rgroup } $$
$$P_{L, Max} = \frac{250}{3} W$$
Par conséquent, la maximum power qui sera fournie à la résistance de charge RL du circuit donné est $\mathbf {\frac{250}{3}}$ W
Si la sortie d'un circuit électrique pour une entrée varie en fonction du temps, alors elle est appelée comme time response. La réponse temporelle comprend les deux parties suivantes.
- Réponse transitoire
- Réponse en régime permanent
Dans ce chapitre, discutons d'abord de ces deux réponses, puis observons ces deux réponses dans un circuit série RL, lorsqu'il est excité par une source de tension continue.
Réponse transitoire
Après avoir appliqué une entrée à un circuit électrique, la sortie prend un certain temps pour atteindre un état stable. Ainsi, la sortie sera dans un état transitoire jusqu'à ce qu'elle passe à un état stable. Par conséquent, la réponse du circuit électrique pendant l'état transitoire est connue sous le nom detransient response.
La réponse transitoire sera nulle pour les grandes valeurs de «t». Idéalement, cette valeur de «t» devrait être l'infini. Mais, pratiquementfive time constants suffisent.
Présence ou absence de transitoires
Des transitoires se produisent dans la réponse en raison de sudden changedans les sources qui sont appliquées au circuit électrique et / ou en raison de l'action de commutation. Il existe deux actions de commutation possibles. Ce sont l'interrupteur d'ouverture et l'interrupteur de fermeture.
le transient une partie sera not presenten réponse à un circuit ou réseau électrique, s'il ne contient que des résistances. Carresistor a la capacité d'ajuster n'importe quelle quantité de tension et de courant.
le transient part occurs en réponse à un circuit ou réseau électrique en raison de la présence d'éléments de stockage d'énergie tels que inductor and capacitor. Parce qu'ils ne peuvent pas changer instantanément l'énergie stockée dans ces éléments.
Comportement de l'inducteur
Supposons que l'action de commutation a lieu à t = 0.Inductor currentne change pas instantanément, lorsque l'action de commutation a lieu. Cela signifie que la valeur du courant d'inductance juste après l'action de commutation sera la même que celle juste avant l'action de commutation.
Mathématiquement, il peut être représenté comme
$$i_L (0^+) = i_L (0^-)$$
Comportement du condensateur
le capacitor voltagene change pas instantanément de la même manière que le courant de l'inducteur, lorsque l'action de commutation a lieu. Cela signifie que la valeur de la tension du condensateur juste après l'action de commutation sera la même que celle juste avant l'action de commutation.
Mathématiquement, il peut être représenté comme
$$v_c (0^+) = v_c (0^-)$$
Réponse en régime permanent
La partie de la réponse temporelle qui reste même après que la réponse transitoire est devenue une valeur nulle pour les grandes valeurs de `` t '' est appelée steady state response. Cela signifie qu'il n'y aura pas de partie transitoire dans la réponse en régime permanent.
Comportement de l'inducteur
Si la source indépendante est connectée au circuit électrique ou au réseau ayant une ou plusieurs inductances et résistances (facultatives) pendant une longue période, alors ce circuit ou réseau électrique est dit en régime permanent. Par conséquent, l'énergie stockée dans le ou les inducteurs de ce circuit électrique est maximale et constante.
Mathématiquement, il peut être représenté comme
$W_L = \frac{L {i_L}^2}{2} = $ Maximum et constant
$\Rightarrow i_L = $ Maximum et constant
Par conséquent, l'inducteur agit comme un constant current source en état d'équilibre.
La tension aux bornes de l'inducteur sera
$$V_L = L \frac{di_{L}}{dt} = 0V$$
Ainsi, l'inducteur agit comme un short circuit en état d'équilibre.
Comportement du condensateur
Si la source indépendante est connectée au circuit électrique ou au réseau ayant un ou plusieurs condensateurs et résistances (facultatifs) pendant une longue période, alors ce circuit ou réseau électrique est dit en état stationnaire. Par conséquent, l'énergie stockée dans le (s) condensateur (s) de ce circuit électrique est maximale et constante.
Mathématiquement, il peut être représenté comme
$W_c = \frac{C{v_c}^2}{2} = $ Maximum et constant
$\Rightarrow v_c = $Maximum et constant
Par conséquent, le condensateur agit comme un constant voltage source en état d'équilibre.
Le courant traversant le condensateur sera
$$i_c = C\frac{dv_c}{dt} = 0A$$
Ainsi, le condensateur agit comme un open circuit en état d'équilibre.
Recherche de la réponse du circuit série RL
Considérer ce qui suit series RL circuit diagramme.
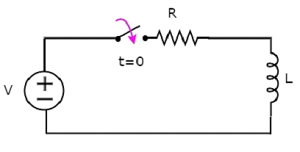
Dans le circuit ci-dessus, le switch était gardé openjusqu'à t = 0 et il était fermé à t = 0. Ainsi, la source de tension continue de V volts n'est pas connectée au circuit série RL jusqu'à cet instant. Par conséquent, il y ano initial current traverse l'inducteur.
Le schéma de circuit, lorsque le switch est dans closed la position est indiquée dans la figure suivante.
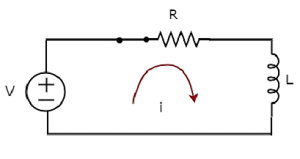
Maintenant, le courant i circule dans tout le circuit, la source de tension continue ayant V volts est connecté au circuit série RL.
Maintenant, postulez KVL autour de la boucle.
$$V = Ri + L \frac{di}{dt}$$
$\frac{di}{dt} + \lgroup \frac{R}{L} \rgroup i = \frac{V}{L}$Equation 1
L'équation ci-dessus est une équation différentielle du premier ordre et se présente sous la forme de
$\frac{dy}{dt} + Py = Q$Equation 2
Par comparing Équation 1 et équation 2, nous obtiendrons les relations suivantes.
$$x = t$$
$$y = i$$
$$P = \frac{R}{L}$$
$$Q = \frac{V}{L}$$
le solution de l'équation 2 sera
$ye^{\int p dx} = \int Q e^{\int p dx} dx + k$Equation 3
Où, k est la constante.
Remplacez, les valeurs de x, y, P et Q dans l'équation 3.
$ie^{\int {\lgroup \frac{R}{L} \rgroup}dt} = \int (\frac{V}{L}) \lgroup e^{\int {\lgroup \frac{R}{L} \rgroup}dt} \rgroup dt + k$
$\Rightarrow ie^{\lgroup \frac{R}{L} \rgroup t} = \frac{V}{L} \int e^{\lgroup \frac{R}{L} \rgroup t} dt + k$
$\Rightarrow ie^{\lgroup \frac{R}{L} \rgroup t} = \frac{V}{L} \lbrace \frac{e^{\lgroup \frac{R}{L} \rgroup}t}{\frac{R}{L}} \rbrace + k$
$\Rightarrow i = \frac{V}{R} + k e^{-\lgroup \frac{R}{L} \rgroup}t$Equation 4
Nous savons qu'il n'y a pas de courant initial dans le circuit. Par conséquent, remplacez, t = 0 et = 0 dans l'équation 4 afin de trouver la valeur de la constante k.
$$0 = \frac{V}{R} + ke^{-\lgroup \frac{R}{L} \rgroup(0)}$$
$$0 = \frac{V}{R} + k(1)$$
$$k = - \frac{V}{R}$$
Remplacez, la valeur de k dans l'équation 4.
$$i = \frac{V}{R} + \lgroup - \frac{V}{R} \rgroup e^{-\lgroup \frac{R}{L} \rgroup t}$$
$$i = \frac{V}{R} - \frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t}$$
Par conséquent, la current circulant dans le circuit est
$i = - \frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t} + \frac{V}{R}$Equation 5
Ainsi, la réponse du circuit série RL, lorsqu'il est excité par une source de tension continue, a les deux termes suivants.
Le premier terme $-\frac{V}{R}e^{-\lgroup \frac{R}{L} \rgroup t}$ correspond à la transient response.
Le deuxième terme $\frac{V}{R}$ correspond à la steady state response. Ces deux réponses sont illustrées dans la figure suivante.
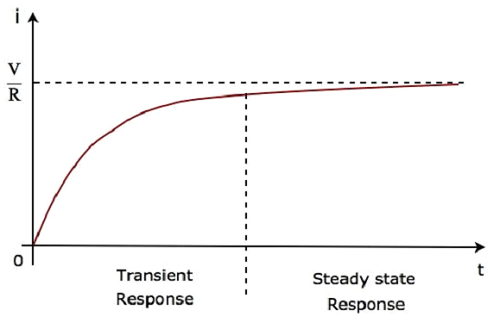
Nous pouvons réécrire l'équation 5 comme suit -
$i = \frac{V}{R} \lgroup 1 - e^{-\lgroup \frac{R}{L} \rgroup t} \rgroup$
$\Rightarrow i = \frac{V}{R} \lgroup 1 - e^{-\lgroup \frac{t}{\tau} \rgroup} \rgroup$Equation 6
Où, τ est le time constant et sa valeur est égale à $\frac{L}{R}$.
L'équation 5 et l'équation 6 sont identiques. Mais, nous pouvons facilement comprendre la forme d'onde ci-dessus du courant circulant dans le circuit à partir de l'équation 6 en substituant quelques valeurs det comme 0, τ, 2τ, 5τ, etc.
Dans la forme d'onde ci-dessus du courant circulant dans le circuit, la réponse transitoire présentera jusqu'à cinq constantes de temps à partir de zéro, tandis que la réponse en régime permanent présentera à partir de cinq constantes de temps.
Dans le chapitre précédent, nous avons discuté de la réponse transitoire et de la réponse en régime permanent du circuit CC. Dans ce chapitre, parlons de laresponse of AC circuit. Les concepts de réponse transitoire et de réponse en régime permanent, dont nous avons discuté dans le chapitre précédent, seront également utiles ici.
Recherche de la réponse du circuit série RL
Considérer ce qui suit series RL circuit diagramme.

Dans le circuit ci-dessus, le switch était gardé openjusqu'à t = 0 et il a été fermé à t = 0 . Ainsi, la source de tension alternative ayant une tension de crête de V m volts n'est pas connectée au circuit série RL jusqu'à cet instant. Par conséquent, il y ano initial current traverse l'inducteur.
Le schéma de circuit, lorsque le switch est dans closed position, est illustré dans la figure suivante.
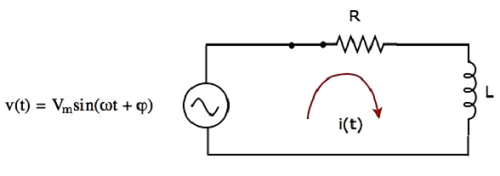
Or, le courant i (t) circule dans tout le circuit, puisque la source de tension alternative ayant une tension de crête de V m volts est connectée au circuit série RL.
Nous savons que le courant i (t) circulant dans le circuit ci-dessus aura deux termes, l'un qui représente la partie transitoire et l'autre terme représente l'état stationnaire.
Mathématiquement, il peut être représenté comme
$i(t) = i_{Tr}(t) + i_{ss}(t)$Equation 1
Où,
$i_{Tr}(t)$ est la réponse transitoire du courant traversant le circuit.
$i_{ss}(t)$ est la réponse en régime permanent du courant circulant dans le circuit.
Dans le chapitre précédent, nous avons obtenu la réponse transitoire du courant traversant le circuit série RL. C'est sous la forme de$Ke^{-\lgroup \frac{t}{\tau} \rgroup}$.
Remplacer $i_{Tr}(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup}$ dans l'équation 1.
$i(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup} + i_{ss}(t)$Equation 2
Calcul du courant à l'état d'équilibre
Si un signal sinusoïdal est appliqué en tant qu'entrée à un circuit électrique linéaire, il produit une sortie en régime permanent, qui est également un sinusoidal signal. Les signaux sinusoïdaux d'entrée et de sortie auront la même fréquence, mais des amplitudes et des angles de phase différents.
Nous pouvons calculer la réponse en régime permanent d'un circuit électrique, lorsqu'il est excité par une source de tension sinusoïdale en utilisant Laplace Transform approach.
Le schéma de circuit du domaine s, lorsque le switch est dans closed position, est illustré dans la figure suivante.
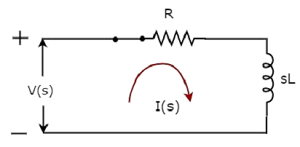
Dans le circuit ci-dessus, toutes les grandeurs et paramètres sont représentés en s-domain. Ce sont les transformées de Laplace des grandeurs et paramètres du domaine temporel.
le Transfer function du circuit ci-dessus est
$$H(s) = \frac{I(s)}{V(s)}$$
$$\Rightarrow H(s) = \frac{1}{Z(s)}$$
$$\Rightarrow H(s) = \frac{1}{R + sL}$$
Remplacer $s = j \omega$ dans l'équation ci-dessus.
$$H(j \omega) = \frac{1}{R + j \omega L}$$
Magnitude of $\mathbf{\mathit{H(j \omega)}}$ est
$$|H(j \omega)| = \frac{1}{\sqrt{R^2 + {\omega}^2}L^2}$$
Phase angle of $\mathbf{\mathit{H(j \omega)}}$ est
$$\angle H(j \omega) = -tan^{-1} \lgroup \frac{\omega L}{R} \rgroup$$
Nous obtiendrons le steady state current $i_{ss}(t)$ en effectuant les deux étapes suivantes -
Multipliez la tension de crête de la tension sinusoïdale d'entrée et l'amplitude de $H(j \omega)$.
Ajouter les angles de phase de la tension sinusoïdale d'entrée et $H(j \omega)$.
le steady state current $i_{ss}(t)$ sera
$$i_{ss}(t) = \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
Remplacez la valeur de $i_{ss}(t)$ dans l'équation 2.
$i(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$Equation 3
Nous savons qu'il n'y a pas de courant initial dans le circuit. Par conséquent, substituez t = 0 & i (t) = 0 dans l'équation 3 afin de trouver la valeur de constante, K.
$$0 = Ke^{-\lgroup \frac{0}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega (0) + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
$$\Rightarrow 0 = K + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
$$\Rightarrow K = - \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
Remplacez la valeur de K dans l'équation 3.
$i(t) = - \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup e^{-\lgroup \frac{t}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$Equation 4
L'équation 4 représente le courant circulant dans le circuit série RL, lorsqu'il est excité par une source de tension sinusoïdale. Il a deux mandats. Les premier et second termes représentent respectivement la réponse transitoire et la réponse en régime permanent du courant.
nous pouvons neglect the first termde l'équation 4 parce que sa valeur sera bien inférieure à un. Ainsi, le courant résultant circulant dans le circuit sera
$$i(t) = \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$
Il ne contient que le steady state term. Par conséquent, nous ne pouvons trouver que la réponse en régime permanent des circuits CA et en négliger la réponse transitoire.
Resonancese produit dans les circuits électriques en raison de la présence d'éléments de stockage d'énergie comme l'inductance et le condensateur. C'est le concept fondamental sur lequel les récepteurs de radio et de télévision sont conçus de manière à ne pouvoir sélectionner que la fréquence de la station souhaitée.
Il y a two typesde résonances, à savoir résonance série et résonance parallèle. Ceux-ci sont classés en fonction des éléments du réseau connectés en série ou en parallèle. Dans ce chapitre, parlons de la résonance des séries.
Schéma du circuit de résonance en série
Si la résonance se produit dans un circuit RLC série, elle est appelée Series Resonance. Considérer ce qui suitseries RLC circuit, qui est représenté dans le domaine du phaseur.
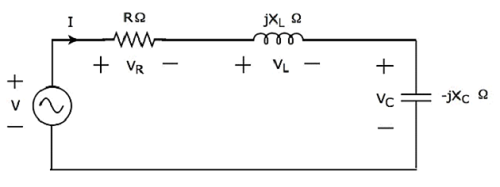
Ici, les éléments passifs tels que la résistance, l'inductance et le condensateur sont connectés en série. Toute cette combinaison est enseries avec la source de tension sinusoïdale d'entrée.
Appliquer KVL autour de la boucle.
$$V - V_R - V_L - V_C = 0$$
$$\Rightarrow V - IR - I(j X_L) - I(-j X_C) = 0$$
$$\Rightarrow V = IR + I(j X_L) + I(-j X_C)$$
$\Rightarrow V = I[R + j(X_L - X_C)]$Equation 1
L'équation ci-dessus est sous la forme de V = IZ.
Par conséquent, la impedance Z du circuit RLC série sera
$$Z = R + j(X_L - X_C)$$
Paramètres et grandeurs électriques à la résonance
Maintenant, dérivons les valeurs des paramètres et des grandeurs électriques à la résonance du circuit série RLC une par une.
Fréquence de résonance
La fréquence à laquelle se produit la résonance est appelée resonant frequency fr. En série, la résonance du circuit RLC se produit lorsque le terme imaginaire de l'impédance Z est nul, c'est-à-dire la valeur de$X_L - X_C$ doit être égal à zéro.
$$\Rightarrow X_L = X_C$$
Remplacer $X_L = 2 \pi f L$ et $X_C = \frac{1}{2 \pi f C}$ dans l'équation ci-dessus.
$$2 \pi f L = \frac{1}{2 \pi f C}$$
$$\Rightarrow f^2 = \frac{1}{(2 \pi)^2 L C}$$
$$\Rightarrow f = \frac{1}{(2 \pi) \sqrt{LC}}$$
Par conséquent, la resonant frequency fr du circuit RLC série est
$$f_r = \frac{1}{(2 \pi) \sqrt{LC}}$$
Où, L est l'inductance d'un inducteur et C est la capacité d'un condensateur.
le resonant frequency fr du circuit RLC série ne dépend que de l'inductance L et capacité C. Mais, c'est indépendant de la résistanceR.
Impédance
Nous avons le impedance Z du circuit RLC série comme
$$Z = R + j(X_L - X_C)$$
Remplacer $X_L = X_C$ dans l'équation ci-dessus.
$$Z = R + j(X_C - X_C)$$
$$\Rightarrow Z = R + j(0)$$
$$\Rightarrow Z = R$$
À la résonance, le impedance Z du circuit RLC série est égal à la valeur de la résistance R, c'est à dire, Z = R.
Courant circulant dans le circuit
Remplacer $X_L - X_C = 0$ dans l'équation 1.
$$V = I[R + j(0)]$$
$$\Rightarrow V = IR$$
$$\Rightarrow I = \frac{V}{R}$$
Par conséquent, current circulant à travers le circuit RLC série à la résonance est $\mathbf{\mathit{I = \frac{V}{R}}}$.
À la résonance, l'impédance du circuit RLC série atteint sa valeur minimale. D'où lemaximum current traverse ce circuit à la résonance.
Tension à travers la résistance
La tension aux bornes de la résistance est
$$V_R = IR$$
Remplacez la valeur de I dans l'équation ci-dessus.
$$V_R = \lgroup \frac{V}{R} \rgroup R$$
$$\Rightarrow V_R = V$$
Par conséquent, la voltage across resistor à la résonance est VR = V.
Tension à travers l'inducteur
La tension aux bornes de l'inducteur est
$$V_L = I(jX_L)$$
Remplacez la valeur de I dans l'équation ci-dessus.
$$V_L = \lgroup \frac{V}{R} \rgroup (jX_L)$$
$$\Rightarrow V_L = j \lgroup \frac{X_L}{R} \rgroup V$$
$$\Rightarrow V_L = j QV$$
Par conséquent, la voltage across inductor à la résonance est $V_L = j QV$.
Alors le magnitude de tension aux bornes de l'inductance à la résonance sera
$$|V_L| = QV$$
Où Q est le Quality factor et sa valeur est égale à $\frac{X_L}{R}$
Tension à travers le condensateur
La tension aux bornes du condensateur est
$$V_C = I(-j X_C)$$
Remplacez la valeur de I dans l'équation ci-dessus.
$$V_C = \lgroup \frac{V}{R} \rgroup (-j X_C)$$
$$\Rightarrow V_C = -j \lgroup \frac{X_C}{R} \rgroup V$$
$$\Rightarrow V_C = -jQV$$
Par conséquent, la voltage across capacitor à la résonance est $\mathbf{\mathit{V_C = -jQV}}$.
Alors le magnitude de tension aux bornes du condensateur à la résonance sera
$$|V_C| = QV$$
Où Q est le Quality factor et sa valeur est égale à $\frac{X_{C}}{R}$
Note - Le circuit RLC de résonance en série est appelé voltage magnificationcircuit, parce que l'amplitude de tension aux bornes de l'inductance et le condensateur est égale à Q fois la tension sinusoïdale d' entrée V .
Dans le chapitre précédent, nous avons discuté de l'importance de la résonance des séries. Parlons maintenant de la résonance parallèle dans les circuits RLC.
Schéma du circuit de résonance parallèle
Si la résonance se produit dans un circuit RLC parallèle, elle est appelée Parallel Resonance. Considérer ce qui suitparallel RLC circuit, qui est représenté dans le domaine du phaseur.
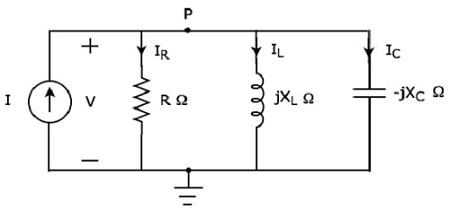
Ici, les éléments passifs tels que la résistance, l'inductance et le condensateur sont connectés en parallèle. Toute cette combinaison est enparallel avec la source de courant sinusoïdal d'entrée.
Écrire nodal equation au nœud P.
$$- I + I_R + I_L + I_C = 0$$
$$\Rightarrow - I + \frac{V}{R} + \frac{V}{j X_L} + \frac{V}{-j X_C} = 0$$
$$\Rightarrow I = \frac{V}{R} - \frac{jV}{X_L} + \frac{jV}{X_C}$$
$\Rightarrow I = V[\frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_L} \rgroup]$Equation 1
L'équation ci-dessus est sous la forme de I = VY.
Par conséquent, la admittance Y du circuit RLC parallèle sera
$$Y = \frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_L} \rgroup$$
Paramètres et grandeurs électriques à la résonance
Maintenant, dérivons les valeurs des paramètres et des grandeurs électriques à la résonance du circuit RLC parallèle une par une.
Fréquence de résonance
Nous savons que le resonant frequency, frest la fréquence à laquelle la résonance se produit. Dans le circuit RLC parallèle, la résonance se produit, lorsque le terme imaginaire d'admittance, Y est nul. c'est-à-dire la valeur de$\frac{1}{X_C} - \frac{1}{X_L}$ devrait être égal à zéro
$$\Rightarrow \frac{1}{X_C} = \frac{1}{X_L}$$
$$\Rightarrow X_L = X_C$$
La condition de résonance ci-dessus est la même que celle du circuit RLC série. Alors leresonant frequency, fr sera le même dans le circuit RLC série et le circuit RLC parallèle.
Par conséquent, la resonant frequency, fr du circuit RLC parallèle est
$$f_r = \frac{1}{2 \pi \sqrt{LC}}$$
Où,
- L est l'inductance d'un inducteur.
- C est la capacité d'un condensateur.
le resonant frequency, fr du circuit RLC parallèle ne dépend que de l'inductance L et capacité C. Mais, c'est indépendant de la résistanceR.
Admission
Nous avons le admittance Y du circuit RLC parallèle comme
$$Y = \frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_L} \rgroup$$
Remplacer, $X_L = X_C$ dans l'équation ci-dessus.
$$Y = \frac{1}{R} + j \lgroup \frac{1}{X_C} - \frac{1}{X_C} \rgroup$$
$$\Rightarrow Y = \frac{1}{R} + j(0)$$
$$\Rightarrow Y = \frac{1}{R}$$
À la résonance, le admittance, Y du circuit RLC parallèle est égal à l'inverse de la résistance, R. c'est-à-dire, $\mathbf{\mathit{Y = \frac{1}{R}}}$
Tension à travers chaque élément
Remplacer, $\frac{1}{X_C} - \frac{1}{X_L} = 0$ dans l'équation 1
$$I = V [\frac{1}{R} + j(0)]$$
$$\Rightarrow I = \frac{V}{R}$$
$$\Rightarrow V = IR$$
Par conséquent, la voltage à travers tous les éléments du circuit RLC parallèle à la résonance est V = IR.
À la résonance, l'admittance du circuit RLC parallèle atteint la valeur minimale. Par conséquent,maximum voltage est présent à travers chaque élément de ce circuit à la résonance.
Courant traversant la résistance
Le courant traversant la résistance est
$$I_R = \frac{V}{R}$$
Remplacez la valeur de V dans l'équation ci-dessus.
$$I_R = \frac{IR}{R}$$
$$\Rightarrow I_R = I$$
Par conséquent, la current flowing through resistor à la résonance est $\mathbf{\mathit{I_R = I}}$.
Courant circulant à travers l'inducteur
Le courant traversant l'inducteur est
$$I_L = \frac{V}{j X_L}$$
Remplacez la valeur de V dans l'équation ci-dessus.
$$I_L = \frac{IR}{j X_L}$$
$$\Rightarrow I_L = -j \lgroup \frac{R}{X_L} \rgroup I$$
$$\Rightarrow I_L = -jQI$$
Par conséquent, la current flowing through inductor à la résonance est $I_L = -jQI$.
Alors le magnitude du courant traversant l'inducteur à la résonance sera
$$|I_L| = QI$$
Où, Q est le Quality factor et sa valeur est égale à $\frac{R}{X_L}$
Courant traversant le condensateur
Le courant traversant le condensateur est
$$I_C = \frac{V}{-j X_C}$$
Remplacez la valeur de V dans l'équation ci-dessus.
$$I_C = \frac{IR}{-j X_C}$$
$$\Rightarrow I_C = j \lgroup \frac{R}{X_C} \rgroup I$$
$$\Rightarrow I_C = jQI$$
Par conséquent, la current flowing through capacitor à la résonance est $I_C = jQI$
Alors le magnitude du courant traversant le condensateur à la résonance sera
$$|I_C| = QI$$
Où, Q est le Quality factor et sa valeur est égale à $\frac{R}{X_C}$
Note - Le circuit RLC à résonance parallèle est appelé current magnificationcircuit. Parce que l'amplitude du courant circulant à travers l' inductance et le condensateur est égale à Q fois l'entrée sinusoïdale de courant I .
On dit qu'un circuit électrique est un coupled circuit, lorsqu'il existe une inductance mutuelle entre les bobines (ou inductances) présentes dans ce circuit. La bobine n'est rien d'autre que la combinaison en série d'une résistance et d'un inducteur. En l'absence de résistance, la bobine devient inductance. Parfois, les termes bobine et inducteur sont utilisés de manière interchangeable.
Dans ce chapitre, parlons d'abord de la convention de point, puis de la classification du couplage.
Convention de points
La convention de points est une technique qui donne des détails sur la polarité de la tension à la borne pointillée. Ces informations sont utiles lors de l'écriture d'équations KVL.
Si le courant entre à la borne pointillée d'une bobine (ou inductance), alors il induit une tension à une autre bobine (ou inductance), qui a positive polarity au terminal pointillé.
Si le courant part de la borne en pointillé d'une bobine (ou inductance), alors il induit une tension à une autre bobine (ou inductance), qui a negative polarity au terminal pointillé.
Classification de l'accouplement
Nous pouvons classer coupling dans les deux catégories suivantes.
- Couplage électrique
- Accouplement magnétique
Maintenant, parlons de chaque type de couplage un par un.
Couplage électrique
Le couplage électrique se produit, lorsqu'il existe un physical connectionentre deux bobines (ou inducteurs). Ce couplage peut être de type auxiliaire ou de type opposé. Il est basé sur le fait que le courant entre à la borne pointillée ou sort de la borne pointillée.
Accouplement de type Aiding
Considérez le circuit électrique suivant, qui a deux inducteurs connectés en series.
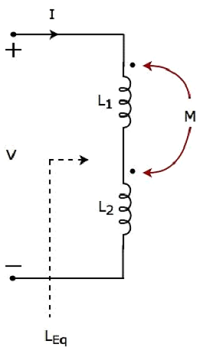
Puisque les deux inducteurs sont connectés en série, le same current Icirculent à travers les deux inductances ayant des self-inductances L 1 et L 2 .
Dans ce cas, le courant, j'entre à la borne pointillée de chaque inducteur. Par conséquent, la tension induite dans chaque inducteur aurapositive polarity à la borne pointillée en raison du courant circulant dans une autre bobine.
Appliquer KVL autour de la boucle du circuit électrique ou du réseau ci-dessus.
$$V - L_1 \frac{dI}{dt} - M \frac{dI}{dt} - L_2 \frac{dI}{dt} - M \frac{dI}{dt} = 0$$
$$V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} + 2M \frac{dI}{dt}$$
$$V = (L_1 + L_2 + 2M)\frac{dI}{dt}$$
L'équation ci-dessus est sous la forme de $\mathbf{\mathit{V = L_{Eq} \frac{dI}{dt}}}$
Par conséquent, la equivalent inductance de la combinaison en série d'inducteurs montrés dans la figure ci-dessus est
$$L_{Eq} = L_1 + L_2 + 2M$$
Dans ce cas, l'inductance équivalente a été augmentée de 2M. Par conséquent, le circuit électrique ci-dessus est un exemple deelectrical couplage qui est de aiding type.
Accouplement de type opposé
Considérez le circuit électrique suivant, qui a deux inducteurs connectés en series.
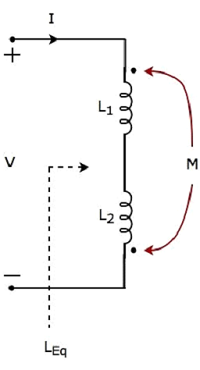
Dans le circuit ci-dessus, le courant I entre à la borne pointillée de l'inducteur ayant une inductance de L1. Par conséquent, il induit une tension dans l'autre inducteur ayant une inductance deL2. Alors,positive polarity de la tension induite est présente à la borne en pointillé de cet inducteur.
Dans le circuit ci-dessus, le courant I feuilles de la borne en pointillé de l'inducteur ayant une inductance de L2. Par conséquent, il induit une tension dans l'autre inducteur ayant une inductance deL1. Alors,negative polarity de la tension induite est présente à la borne en pointillé de cet inducteur.
Appliquer KVL autour de la boucle du circuit électrique ou du réseau ci-dessus.
$$V - L_1 \frac{dI}{dt} + M \frac{dI}{dt} - L_2 \frac{dI}{dt} + M \frac{dI}{dt} = 0$$
$$\Rightarrow V = L_1 \frac{dI}{dt} + L_2 \frac{dI}{dt} - 2M \frac{dI}{dt}$$
$$\Rightarrow V = (L_1 + L_2 - 2M)\frac{dI}{dt}$$
L'équation ci-dessus est sous la forme de $\mathbf{\mathit{V = L_{Eq} \frac{dI}{dt}}}$
Par conséquent, la equivalent inductance de la combinaison en série d'inducteurs montrés dans la figure ci-dessus est
$$L_{Eq} = L_1 + L_2 - 2M$$
Dans ce cas, l'inductance équivalente a été diminuée de 2M. Par conséquent, le circuit électrique ci-dessus est un exemple deelectrical couplage qui est de opposing type.
Accouplement magnétique
Le couplage magnétique se produit, lorsqu'il y a no physical connectionentre deux bobines (ou inducteurs). Ce couplage peut être de type auxiliaire ou de type opposé. Il est basé sur le fait que le courant entre à la borne pointillée ou sort de la borne pointillée.
Accouplement de type Aiding
Considérez l'équivalent électrique suivant circuit of transformer. Il a deux bobines et celles-ci sont appelées bobines primaires et secondaires.
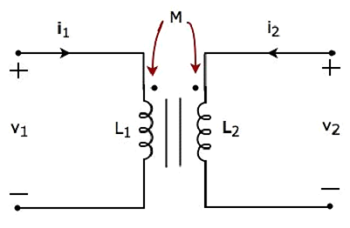
Les courants circulant dans les bobines primaire et secondaire sont respectivement i 1 et i 2 . Dans ce cas, ces courantsenterà la borne pointillée de la bobine respective. Par conséquent, la tension induite dans chaque bobine aura une polarité positive à la borne en pointillé en raison du courant circulant dans une autre bobine.
Appliquer KVL autour de la bobine primaire.
$$v_1 - L_1 \frac{d i_1}{dt} - M \frac{d i_2}{dt} = 0$$
$\Rightarrow v_1 = L_1 \frac{d i_1}{dt} + M \frac{d i_2}{dt}$Equation 1
Appliquer KVL autour de la bobine secondaire.
$$v_2 - L_2 \frac{d i_2}{dt} - M \frac{d i_1}{dt} = 0$$
$\Rightarrow v_2 = L_2 \frac{d i_2}{dt} + M \frac{d i_1}{dt}$Equation 2
Dans l'équation 1 et l'équation 2, la tension auto-induite et la tension induite mutuellement ont la même polarité. Par conséquent, le circuit de transformateur ci-dessus est un exemple demagnetic coupling, qui est de aiding type.
Accouplement de type opposé
Considérez l'équivalent électrique suivant circuit of transformer.

Les courants circulant dans les bobines primaire et secondaire sont respectivement i 1 et i 2 . Dans ce cas, le courant, i 1 entre à la borne en pointillé de la bobine primaire. Par conséquent, il induit une tension dans la bobine secondaire. Alors,positive polarity de la tension induite est présente à la borne en pointillé de cette bobine secondaire.
Dans le circuit ci-dessus, le courant, i 2 part de la borne en pointillé de la bobine secondaire. Par conséquent, il induit une tension dans la bobine primaire. Alors,negative polarity de la tension induite est présente à la borne en pointillé de cette bobine primaire.
Appliquer KVL autour de la bobine primaire.
$$v_1 - L_1 \frac{d i_1}{dt} + M \frac{d i_2}{dt} = 0$$
$\Rightarrow v_1 = L_1 \frac{d i_1}{dt} - M \frac{d i_2}{dt}$Equation 3
Appliquer KVL autour de la bobine secondaire.
$$v_2 - L_2 \frac{d i_2}{dt} + M \frac{d i_1}{dt} = 0$$
$\Rightarrow v_2 = L_2 \frac{d i_2}{dt} - M \frac{d i_1}{dt}$Equation 4
Dans l'équation 3 et l'équation 4, la tension auto-induite et la tension induite mutuellement ont une polarité opposée. Par conséquent, le circuit de transformateur ci-dessus est un exemple demagnetic coupling, qui est de opposing type.
En général, il est facile d'analyser n'importe quel réseau électrique, s'il est représenté avec un modèle équivalent, qui donne la relation entre les variables d'entrée et de sortie. Pour cela, nous pouvons utilisertwo port networkreprésentations. Comme son nom l'indique, deux réseaux de ports contiennent deux ports. Parmi eux, un port est utilisé comme port d'entrée et l'autre port est utilisé comme port de sortie. Les premier et second ports sont appelés respectivement port1 et port2.
One port networkest un réseau électrique à deux terminaux dans lequel le courant entre par un terminal et sort par un autre terminal. Les résistances, inductances et condensateurs sont les exemples d'un réseau à un port car chacun a deux bornes. Une représentation de réseau de port est illustrée dans la figure suivante.
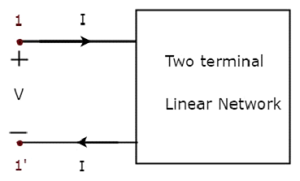
Ici, la paire de terminaux, 1 & 1 'représente un port. Dans ce cas, nous n'avons qu'un seul port puisqu'il s'agit d'un réseau à un port.
De même, two port networkest une paire de réseau électrique à deux terminaux dans lequel le courant entre par un terminal et sort par un autre terminal de chaque port. La représentation du réseau à deux ports est illustrée dans la figure suivante.
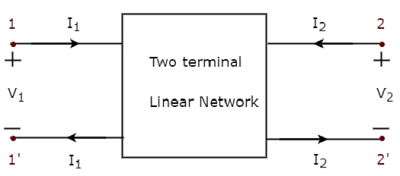
Ici, une paire de terminaux, 1 & 1 'représente un port, qui est appelé comme port1 et l'autre paire de terminaux, 2 & 2 'représente un autre port, qui est appelé comme port2.
Il y a four variablesV 1 , V 2 , I 1 et I 2 dans un réseau à deux ports comme indiqué sur la figure. À partir de laquelle, nous pouvons choisir deux variables comme indépendantes et deux autres variables comme dépendantes. Ainsi, nous obtiendrons six paires d'équations possibles. Ces équations représentent les variables dépendantes en termes de variables indépendantes. Les coefficients des variables indépendantes sont appelés commeparameters. Ainsi, chaque paire d'équations donnera un ensemble de quatre paramètres.
Paramètres de réseau à deux ports
Les paramètres d'un réseau à deux ports sont appelés two port network parametersou simplement, deux paramètres de port. Voici les types de paramètres réseau à deux ports.
- Paramètres Z
- Paramètres Y
- Paramètres T
- Paramètres T '
- h-parameters
- g-parameters
Maintenant, laissez-nous discuter de ces deux paramètres de réseau de ports un par un.
Paramètres Z
Nous obtiendrons l'ensemble suivant de deux équations en considérant les variables V 1 & V 2 comme dépendantes et I 1 & I 2 comme indépendantes. Les coefficients des variables indépendantes, I 1 et I 2 sont appelésZ parameters.
$$V_1 = Z_{11} I_1 + Z_{12} I_2$$
$$V_2 = Z_{21} I_1 + Z_{22} I_2$$
le Z parameters sont
$$Z_{11} = \frac{V_1}{I_1}, \: when \: I_2 = 0$$
$$Z_{12} = \frac{V_1}{I_2}, \: when \: I_1 = 0$$
$$Z_{21} = \frac{V_2}{I_1}, \: when \: I_2 = 0$$
$$Z_{22} = \frac{V_2}{I_2}, \: when \: I_1 = 0$$
Les paramètres Z sont appelés comme impedance parameterscar ce sont simplement les rapports des tensions et des courants. Les unités des paramètres Z sont Ohm (Ω).
Nous pouvons calculer deux paramètres Z, Z 11 et Z 21 , en faisant un circuit ouvert du port2. De même, on peut calculer les deux autres paramètres Z, Z 12 et Z 22 en faisant un circuit ouvert du port1. Par conséquent, les paramètres Z sont également appelésopen-circuit impedance parameters.
Paramètres Y
Nous obtiendrons l'ensemble suivant de deux équations en considérant les variables I 1 & I 2 comme dépendantes et V 1 & V 2 comme indépendantes. Les coefficients des variables indépendantes, V 1 et V 2 sont appelésY parameters.
$$I_1 = Y_{11} V_1 + Y_{12} V_2$$
$$I_2 = Y_{21} V_1 + Y_{22} V_2$$
le Y parameters sont
$$Y_{11} = \frac{I_1}{V_1}, \: when \: V_2 = 0$$
$$Y_{12} = \frac{I_1}{V_2}, \: when \: V_1 = 0$$
$$Y_{21} = \frac{I_2}{V_1}, \: when \: V_2 = 0$$
$$Y_{22} = \frac{I_2}{V_2}, \: when \: V_1 = 0$$
Les paramètres Y sont appelés admittance parametersparce que ce sont simplement les rapports des courants et des tensions. Les unités des paramètres Y sont mho.
Nous pouvons calculer deux paramètres Y, Y 11 et Y 21 en faisant un court-circuit du port2. De même, nous pouvons calculer les deux autres paramètres Y, Y 12 et Y 22 en faisant court-circuit du port1. Par conséquent, les paramètres Y sont également appelésshort-circuit admittance parameters.
Paramètres T
Nous obtiendrons l'ensemble suivant de deux équations en considérant les variables V 1 & I 1 comme dépendantes et V 2 & I 2 comme indépendantes. Les coefficients de V 2 et -I 2 sont appelésT parameters.
$$V_1 = A V_2 - B I_2$$
$$I_1 = C V_2 - D I_2$$
le T parameters sont
$$A = \frac{V_1}{V_2}, \: when \: I_2 = 0$$
$$B = -\frac{V_1}{I_2}, \: when \: V_2 = 0$$
$$C = \frac{I_1}{V_2}, \: when \: I_2 = 0$$
$$D = -\frac{I_1}{I_2}, \: when \: V_2 = 0$$
Les paramètres T sont appelés comme paramètres de transmission ou ABCD parameters. Les paramètres A et D n'ont pas d'unité, car ceux-ci sont de dimension inférieure. Les unités de paramètres, B et C sont respectivement ohm et mho.
Nous pouvons calculer deux paramètres, A et C en faisant un circuit ouvert de port2. De même, on peut calculer les deux autres paramètres, B et D en faisant court-circuit du port2.
Paramètres T '
Nous obtiendrons l'ensemble suivant de deux équations en considérant les variables V 2 & I 2 comme dépendantes et V 1 & I 1 comme indépendantes. Les coefficients de V 1 et -I 1 sont appelésT’ parameters.
$$V_2 = A' V_1 - B' I_1$$
$$I_2 = C' V_1 - D' I_1$$
le T’ parameters sont
$$A' = \frac{V_2}{V_1}, \: when\: I_1 = 0$$
$$B' = -\frac{V_2}{I_1}, \: when\: V_1 = 0$$
$$C' = \frac{I_2}{V_1}, \: when\: I_1 = 0$$
$$D' = -\frac{I_2}{I_1}, \: when \: V_1 = 0$$
Les paramètres T 'sont appelés paramètres de transmission inverse ou A’B’C’D’ parameters. Les paramètres A 'et D' n'ont pas d'unité, car ceux-ci sont de dimension inférieure. Les unités de paramètres, B 'et C', sont respectivement Ohm et Mho.
On peut calculer deux paramètres, A 'et C', en faisant un circuit ouvert de port1. De même, on peut calculer les deux autres paramètres, B 'et D', en faisant un court-circuit de port1.
paramètres h
Nous obtiendrons l'ensemble suivant de deux équations en considérant les variables V 1 & I 2 comme dépendantes et I 1 & V 2 comme indépendantes. Les coefficients des variables indépendantes, I 1 et V 2 , sont appelésh-parameters.
$$V_1 = h_{11} I_1 + h_{12} V_2$$
$$I_2 = h_{21} I_1 + h_{22} V_2$$
Les paramètres h sont
$$h_{11} = \frac{V_1}{I_1},\: when\: V_2 = 0$$
$$h_{12} = \frac{V_1}{V_2},\: when\: I_1 = 0$$
$$h_{21} = \frac{I_2}{I_1},\: when\: V_2 = 0$$
$$h_{22} = \frac{I_2}{V_2},\: when\: I_1 = 0$$
Les paramètres h sont appelés comme hybrid parameters. Les paramètres, h 12 et h 21 , n'ont pas d'unité, car ils sont sans dimension. Les unités de paramètres, h 11 et h 22 , sont respectivement Ohm et Mho.
On peut calculer deux paramètres, h 11 et h 21 en faisant court-circuit du port2. De même, on peut calculer les deux autres paramètres, h 12 et h 22 en faisant un circuit ouvert de port1.
Les paramètres h ou paramètres hybrides sont utiles dans les circuits de modélisation de transistors (réseaux).
paramètres g
Nous obtiendrons l'ensemble suivant de deux équations en considérant les variables I 1 & V 2 comme dépendantes et V 1 & I 2 comme indépendantes. Les coefficients des variables indépendantes, V 1 et I 2 sont appelésg-parameters.
$$I_1 = g_{11} V_1 + g_{12} I_2$$
$$V_2 = g_{21} V_1 + g_{22} I_2$$
le g-parameters sont
$$g_{11} = \frac{I_1}{V_1},\: when\: I_2 = 0$$
$$g_{12} = \frac{I_1}{I_2},\: when\: V_1 = 0$$
$$g_{21} = \frac{V_2}{V_1},\: when\: I_2 = 0$$
$$g_{22} = \frac{V_2}{I_2},\: when \: V_1 = 0$$
Les paramètres g sont appelés comme inverse hybrid parameters. Les paramètres g 12 et g 21 n'ont pas d'unité, car ceux-ci sont de dimension inférieure. Les unités de paramètres, g 11 et g 22 sont respectivement mho et ohm.
Nous pouvons calculer deux paramètres, g 11 et g 21 en faisant un circuit ouvert du port2. De même, on peut calculer les deux autres paramètres, g 12 et g 22 en faisant court-circuit du port1.
Dans le chapitre précédent, nous avons discuté de six types de paramètres de réseau à deux ports. Maintenant, convertissons un ensemble de paramètres réseau à deux ports en un autre ensemble de paramètres réseau à deux ports. Cette conversion est connue sous le nom de conversion de paramètres réseau à deux ports ou simplement,two-port parameters conversion.
Parfois, il est facile de trouver facilement un ensemble de paramètres d'un réseau électrique donné. Dans ces situations, nous pouvons convertir ces paramètres en l'ensemble de paramètres requis au lieu de calculer ces paramètres directement avec plus de difficulté.
Maintenant, laissez-nous discuter de certaines des deux conversions de paramètres de port.
Procédure de conversion de deux paramètres de port
Suivez ces étapes tout en convertissant un ensemble de paramètres réseau à deux ports en un autre ensemble de paramètres réseau à deux ports.
Step 1 - Écrivez les équations d'un réseau à deux ports en fonction des paramètres souhaités.
Step 2 - Ecrire les équations d'un réseau à deux ports en termes de paramètres donnés.
Step 3 - Réorganiser les équations de Step2 de manière à ce qu'elles soient similaires aux équations de Step1.
Step 4- En assimilant les équations similaires de Step1 et Step3, nous obtiendrons les paramètres souhaités en termes de paramètres donnés. Nous pouvons représenter ces paramètres sous forme matricielle.
Paramètres Z en paramètres Y
Ici, nous devons représenter les paramètres Y en termes de paramètres Z. Donc, dans ce cas, les paramètres Y sont les paramètres souhaités et les paramètres Z sont les paramètres donnés.
Step 1 - Nous savons que l'ensemble suivant de deux équations, qui représente un réseau à deux ports en termes de Y parameters.
$$I_1 = Y_{11} V_1 + Y_{12} V_2$$
$$I_2 = Y_{21} V_1 + Y_{22} V_2$$
Nous pouvons représenter les deux équations ci-dessus dans matrix forme comme
$\begin{bmatrix}I_1 \\I_2 \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} \begin{bmatrix}V_1 \\V_2 \end{bmatrix}$Equation 1
Step 2 - Nous savons que l'ensemble suivant de deux équations, qui représente un réseau à deux ports en termes de Z parameters.
$$V_1 = Z_{11} I_1 + Z_{12} I_2$$
$$V_2 = Z_{21} I_1 + Z_{22} I_2$$
Nous pouvons représenter les deux équations ci-dessus dans matrix forme comme
$$\begin{bmatrix}V_1 \\V_2 \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} \begin{bmatrix}I_1 \\I_2 \end{bmatrix}$$
Step 3 - Nous pouvons le modifier comme
$\begin{bmatrix}I_1 \\I_2 \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix}^{-1} \begin{bmatrix}V_1 \\V_2 \end{bmatrix}$Equation 2
Step 4 - En mettant l'équation 1 et l'équation 2, nous obtiendrons
$$\begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix}^{-1} $$
$$\Rightarrow \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} = \frac{\begin{bmatrix}Z_{22} & -Z_{12} \\-Z_{21} & Z_{11} \end{bmatrix}}{\Delta Z}$$
Où,
$$\Delta Z = Z_{11} Z_{22} - Z_{12} Z_{21}$$
Donc, juste en faisant le inverse of Z parameters matrix, nous obtiendrons une matrice de paramètres Y.
Paramètres Z en paramètres T
Ici, nous devons représenter les paramètres T en termes de paramètres Z. Donc, dans ce cas, les paramètres T sont les paramètres souhaités et les paramètres Z sont les paramètres donnés.
Step 1 - Nous savons que, l'ensemble suivant de deux équations, qui représente un réseau à deux ports en termes de T parameters.
$$V_1 = A V_2 - B I_2$$
$$I_1 = C V_2 - D I_2$$
Step 2 - Nous savons que l'ensemble suivant de deux équations, qui représente un réseau à deux ports en termes de Z parameters.
$$V_1 = Z_{11} I_1 + Z_{12} I_2$$
$$V_2 = Z_{21} I_1 + Z_{22} I_2$$
Step 3 - Nous pouvons modifier l'équation ci-dessus comme
$$\Rightarrow V_2 - Z_{22} I_2 = Z_{21} I_1$$
$$\Rightarrow I_1 = \lgroup \frac{1}{Z_{21}} \rgroup V_2 - \lgroup \frac{Z_{22}}{Z_{21}} \rgroup I_2$$
Step 4 - L'équation ci-dessus se présente sous la forme de $I_1 = CV_2 − DI_2$. Ici,
$$C = \frac{1}{Z_{21}}$$
$$D = \frac{Z_{22}}{Z_{21}}$$
Step 5 - Remplaçant $I_1$ valeur de l'étape 3 dans $V_1$ équation de l'étape 2.
$$V_1 = Z_{11} \lbrace \lgroup \frac {1}{Z_{12}} \rgroup V_2 - \lgroup \frac {Z_{22}}{Z_{21}} \rgroup I_2 \rbrace + Z_{12} I_2$$
$$\Rightarrow V_1 = \lgroup \frac {Z_{11}}{Z_{21}} \rgroup V_2 - \lgroup \frac{Z_{11} Z_{22} - Z_{12} Z_{21}}{Z_{21}} \rgroup I_2$$
Step 6 - L'équation ci-dessus se présente sous la forme de $V_1 = AV_2 − BI_2$. Ici,
$$A = \frac{Z_{11}}{Z_{21}}$$
$$B = \frac{Z_{11} Z_{22} - Z_{12} Z_{21}}{Z_{21}}$$
Step 7 - Par conséquent, le T parameters matrix est
$$\begin{bmatrix}A & B \\C & D \end{bmatrix} = \begin{bmatrix}\frac{Z_{11}}{Z_{21}} & \frac{Z_{11}Z_{22} - Z_{12}Z_{21}}{Z_{21}} \\\frac{1}{Z_{21}} & \frac{Z_{22}}{Z_{21}} \end{bmatrix}$$
Paramètres Y en paramètres Z
Ici, nous devons représenter les paramètres Z en termes de paramètres Y. Donc, dans ce cas, les paramètres Z sont les paramètres souhaités et les paramètres Y sont les paramètres donnés.
Step 1 - Nous savons que, l'équation matricielle suivante du réseau à deux ports concernant les paramètres Z comme
$\begin{bmatrix}V_1 \\V_2 \end{bmatrix} = \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} \begin{bmatrix}I_1 \\I_2 \end{bmatrix}$Equation 3
Step 2 - Nous savons que, l'équation matricielle suivante du réseau à deux ports concernant les paramètres Y comme
$$\begin{bmatrix}I_1 \\I_2 \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix} \begin{bmatrix}V_1 \\V_2 \end{bmatrix}$$
Step 3 - Nous pouvons le modifier comme
$\begin{bmatrix}V_1 \\V_2 \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix}^{-1} \begin{bmatrix}I_1 \\I_2 \end{bmatrix}$Equation 4
Step 4 - En mettant l'équation 3 et l'équation 4, nous obtiendrons
$$\begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} = \begin{bmatrix}Y_{11} & Y_{12} \\Y_{21} & Y_{22} \end{bmatrix}^{-1}$$
$$\Rightarrow \begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} = \frac{\begin{bmatrix}Y_{22} & - Y_{12} \\- Y_{21} & Y_{11} \end{bmatrix}}{\Delta Y}$$
Où,
$$\Delta Y = Y_{11} Y_{22} - Y_{12} Y_{21}$$
Donc, juste en faisant le inverse of Y parameters matrix, nous obtiendrons la matrice des paramètres Z.
Paramètres Y en paramètres T
Ici, nous devons représenter les paramètres T en termes de paramètres Y. Donc, dans ce cas, les paramètres T sont les paramètres souhaités et les paramètres Y sont les paramètres donnés.
Step 1 - Nous savons que, l'ensemble suivant de deux équations, qui représente un réseau à deux ports en termes de T parameters.
$$V_1 = A V_2 - B I_2$$
$$I_1 = C V_2 - D I_2$$
Step 2 - Nous savons que l'ensemble suivant de deux équations du réseau à deux ports concernant les paramètres Y.
$$I_1 = Y_{11} V_1 + Y_{12} V_2$$
$$I_2 = Y_{21} V_1 + Y_{22} V_2$$
Step 3 - Nous pouvons modifier l'équation ci-dessus comme
$$\Rightarrow I_2 - Y_{22} V_2 = Y_{21} V_1$$
$$\Rightarrow V_1 = \lgroup \frac{- Y_{22}}{Y_{21}} \rgroup V_2 - \lgroup \frac{-1}{Y_{21}} \rgroup I_2$$
Step 4 - L'équation ci-dessus se présente sous la forme de $V_1 = AV_2 − BI_2$. Ici,
$$A = \frac{- Y_{22}}{Y_{21}}$$
$$B = \frac{-1}{Y_{21}}$$
Step 5 - Remplaçant $V_1$ valeur de l'étape 3 dans $I_1$ équation de l'étape 2.
$$I_1 = Y_{11} \lbrace \lgroup \frac{- Y_{22}}{Y_{21}} \rgroup V_2 - \lgroup \frac{-1}{Y_{21}} \rgroup I_2 \rbrace + Y_{12} V_2$$
$$\Rightarrow I_1 = \lgroup \frac {Y_{12} Y_{21} - Y_{11} Y_{22}}{Y_{21}} \rgroup V_2 - \lgroup \frac{- Y_{11}} {Y_{21}} \rgroup I_2$$
Step 6 - L'équation ci-dessus se présente sous la forme de $I_1 = CV_2 − DI_2$. Ici,
$$C = \frac {Y_{12} Y_{21} - Y_{11} Y_{22}}{Y_{21}}$$
$$D = \frac{- Y_{11}} {Y_{21}}$$
Step 7 - Par conséquent, le T parameters matrix est
$$\begin{bmatrix}A & B \\C & D \end{bmatrix} = \begin{bmatrix}\frac{-Y_{22}}{Y_{21}} & \frac{-1}{Y_{21}} \\\frac{Y_{12}Y_{21} - Y_{11}Y_{22}}{Y_{21}} & \frac{-Y_{11}}{Y_{21}} \end{bmatrix}$$
Paramètres T en paramètres h
Ici, nous devons représenter les paramètres h en termes de paramètres T. Donc, dans ce cas, hparameters sont les paramètres souhaités et les paramètres T sont les paramètres donnés.
Step 1 - Nous savons que, ce qui suit h-parameters d'un réseau à deux ports.
$$h_{11} = \frac{V_1}{I_1}, \: when \: V_2 = 0$$
$$h_{12} = \frac{V_1}{V_2}, \: when \: I_1 = 0$$
$$h_{21} = \frac{I_2}{I_1}, \: when \: V_2 = 0$$
$$h_{22} = \frac{I_2}{V_2}, \: when \: I_1 = 0$$
Step 2 - Nous savons que l'ensemble suivant de deux équations du réseau à deux ports concernant T parameters.
$V_1 = A V_2 - B I_2$Equation 5
$I_1 = C V_2 - D I_2$Equation 6
Step 3 - Remplaçant $V_2 = 0$ dans les équations ci-dessus afin de trouver les deux paramètres h, $h_{11}$ et $h_{21}$.
$$\Rightarrow V_1 = -B I_2$$
$$\Rightarrow I_1 = -D I_2$$
Remplacer, $V_1$ et $I_1$ valeurs en paramètre h, $h_{11}$.
$$h_{11} = \frac{-B I_2}{-D I_2}$$
$$\Rightarrow h_{11} = \frac{B}{D}$$
Remplacer $I_1$ valeur en paramètre h $h_{21}$.
$$h_{21} = \frac{I_2}{- D I_2}$$
$$\Rightarrow h_{21} = - \frac{1}{D}$$
Step 4 - Remplaçant $I_1 = 0$ dans la deuxième équation de l'étape 2 afin de trouver le paramètre h $h_{22}$.
$$0 = C V_2 - D I_2$$
$$\Rightarrow C V_2 = D I_2$$
$$\Rightarrow \frac{I_2}{V_2} = \frac{C}{D}$$
$$\Rightarrow h_{22} = \frac{C}{D}$$
Step 5 - Remplaçant $I_2 = \lgroup \frac{C}{D} \rgroup V_2$ dans la première équation de l'étape 2 pour trouver le paramètre h, $h_{12}$.
$$V_1 = A V_2 - B \lgroup \frac{C}{D} \rgroup V_2$$
$$\Rightarrow V_1 = \lgroup \frac{AD - BC}{D} \rgroup V_2$$
$$\Rightarrow \frac{V_1}{V_2} = \frac{AD - BC}{D}$$
$$\Rightarrow h_{12} = \frac{AD - BC}{D}$$
Step 6 - Par conséquent, la matrice des paramètres h est
$$\begin{bmatrix}h_{11} & h_{12} \\h_{21} & h_{22} \end{bmatrix} = \begin{bmatrix}\frac{B}{D} & \frac{AD - BC}{D} \\-\frac{1}{D} & \frac{C}{D} \end{bmatrix}$$
Paramètres h en paramètres Z
Ici, nous devons représenter les paramètres Z en termes de paramètres h. Donc, dans ce cas, les paramètres Z sont les paramètres souhaités et les paramètres h sont les paramètres donnés.
Step 1 - Nous savons que, l'ensemble suivant de deux équations du réseau à deux ports concernant Z parameters.
$$V_1 = Z_{11} I_1 + Z_{12} I_2$$
$$V_2 = Z_{21} I_1 + Z_{22} I_2$$
Step 2 - Nous savons que, l'ensemble suivant de deux équations de réseau à deux ports concernant h-parameters.
$$V_1 = h_{11} I_1 + h_{12} V_2$$
$$I_2 = h_{21} I_1 + h_{22} V_2$$
Step 3 - Nous pouvons modifier l'équation ci-dessus comme
$$\Rightarrow I_2 - h_{21} I_1 = h_{22} V_2$$
$$\Rightarrow V_2 = \frac{I_2 - h_{21} I_1}{h_{22}}$$
$$\Rightarrow V_2 = \lgroup \frac{-h_{21}}{h_{22}} \rgroup I_1 + \lgroup \frac{1}{h_{22}} \rgroup I_2$$
L'équation ci-dessus est sous la forme de $V_2 = Z_{21} I_1 + Z_{22} I_2. Here,$
$$Z_{21} = \frac{-h_{21}}{h_{22}}$$
$$Z_{22} = \frac{1}{h_{22}}$$
Step 4- Remplacez la valeur V 2 dans la première équation de l'étape 2.
$$V_1 = h_{11} I_1 + h_{21} \lbrace \lgroup \frac{-h_{21}}{h_{22}} \rgroup I_1 + \lgroup \frac{1}{h_{22}} \rgroup I_2 \rbrace$$
$$\Rightarrow V_1 = \lgroup \frac{h_{11}h_{22} - h_{12}h_{21}}{h_{22}} \rgroup I_1 + \lgroup \frac{h_{12}}{h_{22}} \rgroup I_2$$
L'équation ci-dessus est sous la forme de $V_1 = Z_{11}I_1 + Z_{12}I_2$. Ici,
$$Z_{11} = \frac{h_{11}h_{22} - h_{12}h_{21}}{h_{22}}$$
$$Z_{12} = \frac{h_{12}}{h_{22}}$$
Step 5 - Par conséquent, la matrice des paramètres Z est
$$\begin{bmatrix}Z_{11} & Z_{12} \\Z_{21} & Z_{22} \end{bmatrix} = \begin{bmatrix}\frac{h_{11}h_{22} - h_{12}h_{21}}{h_{22}} & \frac{h_{12}}{h_{22}} \\\frac{-h_{21}}{h_{22}} & \frac{1}{h_{22}} \end{bmatrix}$$
De cette manière, nous pouvons convertir un ensemble de paramètres en un autre ensemble de paramètres.
Filtres comme son nom l'indique, ils filtrent les composantes de fréquence. Cela signifie qu'ils autorisent certaines composantes de fréquence et / ou rejettent certaines autres composantes de fréquence.
Dans ce chapitre, parlons de la passive filters. Ce sont les circuits électriques ou les réseaux ayant des éléments passifs comme la résistance, l'inductance et le condensateur.
Types de filtres
Les filtres sont principalement classés en four typesbasé sur la bande de fréquences qui autorise et / ou la bande de fréquences qui rejettent. Voici les types de filtres.
- Filtre passe bas
- Filtre passe-haut
- Filtre passe-bande
- Filtre d'arrêt de bande
Filtre passe bas
Filtre passe-bas comme son nom l'indique, il permet (passe) uniquement low frequencyComposants. Cela signifie qu'il rejette (bloque) tous les autres composants haute fréquence.
Le domaine s circuit diagram (réseau) du filtre passe-bas est illustré dans la figure suivante.
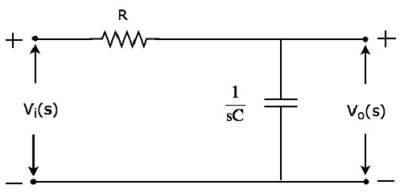
Il se compose de deux éléments passifs résistance et condensateur, qui sont connectés en series. La tension d'entrée est appliquée sur toute cette combinaison et la sortie est considérée comme la tension aux bornes du condensateur.
Ici, $V_i(s)$ et $V_o(s)$ sont les transformées de Laplace de la tension d'entrée, $v_i(t)$ et tension de sortie, $v_o(t)$ respectivement.
le transfer function du réseau ci-dessus est
$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{\frac{1}{sC}}{R + \frac{1}{sC}}$$
$$\Rightarrow H(s) = \frac{1}{1 + sCR}$$
Remplacer, $s = j \omega$ dans l'équation ci-dessus.
$$H(j \omega) = \frac{1}{1 + j \omega CR}$$
L'ampleur de la fonction de transfert est
$$|H(j \omega)| = \frac{1}{\sqrt{(1 + (\omega CR)^2}}$$
À ω = 0, la grandeur de la fonction de transfert est égale à 1.
À $\omega = \frac{1}{CR}$, la grandeur de la fonction de transfert est égale à 0,707.
À ω = ∞, la grandeur de la fonction de transfert est égale à 0.
Par conséquent, l'ampleur de la fonction de transfert de Low pass filtervariera de 1 à 0 car ω varie de 0 à ∞.
Filtre passe-haut
Filtre passe-haut comme son nom l'indique, il permet (passe) uniquement high frequencyComposants. Cela signifie qu'il rejette (bloque) tous les composants basse fréquence.
Le domaine s circuit diagram (réseau) du filtre passe-haut est illustré dans la figure suivante.
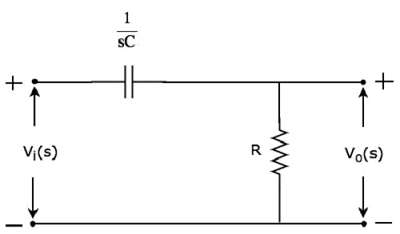
Il se compose de deux éléments passifs condensateur et résistance, qui sont connectés en series. La tension d'entrée est appliquée sur toute cette combinaison et la sortie est considérée comme la tension aux bornes de la résistance.
Ici, $V_i(s)$ et $V_o(s)$ sont les transformées de Laplace de la tension d'entrée, $v_i(t)$ et tension de sortie, $v_o(t)$ respectivement.
le transfer function du réseau ci-dessus est
$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{R}{R + \frac{1}{sC}}$$
$$\Rightarrow H(s) = \frac{sCR}{1 + sCR}$$
Remplacer, $s = j \omega$ dans l'équation ci-dessus.
$$H(j \omega) = \frac{j \omega CR}{1 + j \omega CR}$$
L'ampleur de la fonction de transfert est
$$|H(j \omega)| = \frac{\omega CR}{\sqrt{(1 + (\omega CR)^2}}$$
À ω = 0, la grandeur de la fonction de transfert est égale à 0.
À $\omega = \frac{1}{CR}$, la grandeur de la fonction de transfert est égale à 0,707.
À ω = ∞, la grandeur de la fonction de transfert est égale à 1.
Par conséquent, l'ampleur de la fonction de transfert de High pass filtervariera de 0 à 1 car ω varie de 0 à ∞.
Filtre passe-bande
Filtre passe-bande comme son nom l'indique, il allows (passes) seulement one bandde fréquences. En général, cette bande de fréquences se situe entre la plage des basses fréquences et la plage des hautes fréquences. Cela signifie que ce filtre rejette (bloque) les composants à basse et haute fréquence.
Le domaine s circuit diagram (réseau) du filtre passe-bande est illustré dans la figure suivante.
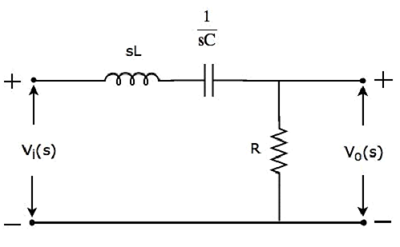
Il se compose de trois éléments passifs inductance, condensateur et résistance, qui sont connectés en series. La tension d'entrée est appliquée sur toute cette combinaison et la sortie est considérée comme la tension aux bornes de la résistance.
Ici, $V_i(s)$ et $V_o(s)$ sont les transformées de Laplace de la tension d'entrée, $v_i(t)$ et tension de sortie, $v_o(t)$ respectivement.
le transfer function du réseau ci-dessus est
$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{R}{R + \frac{1}{sC} + sL}$$
$$\Rightarrow H(s) = \frac{s CR}{s^2 LC + sCR + 1}$$
Remplacer $s = j \omega$ dans l'équation ci-dessus.
$$H(j \omega) = \frac{j \omega CR}{1 - \omega^2 LC + j \omega CR}$$
L'ampleur de la fonction de transfert est
$$|H(j \omega)| = \frac{\omega CR}{\sqrt{(1 - \omega^2 LC)^2 + (\omega CR)^2}}$$
À ω = 0, la grandeur de la fonction de transfert est égale à 0.
À $\omega = \frac{1}{\sqrt{LC}}$, la grandeur de la fonction de transfert est égale à 1.
À ω = ∞, la grandeur de la fonction de transfert est égale à 0.
Par conséquent, l'ampleur de la fonction de transfert de Band pass filtervariera de 0 à 1 & 1 à 0 car ω varie de 0 à ∞.
Filtre d'arrêt de bande
Filtre coupe-bande comme son nom l'indique, il ne rejette (bloque) qu'une seule bande de fréquences. En général, cette bande de fréquences se situe entre la plage des basses fréquences et la plage des hautes fréquences. Cela signifie que ce filtre permet (laisse passer) les composants à basse et haute fréquence.
Le s-domain (réseau) de circuit diagramet le filtre d'arrêt est illustré dans la figure suivante.
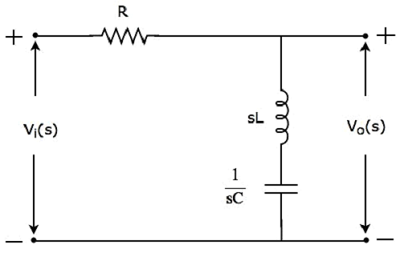
Il se compose de trois éléments passifs résistance, inductance et condensateur, qui sont connectés en series. La tension d'entrée est appliquée à travers toute cette combinaison et la sortie est considérée comme la tension à travers la combinaison de l'inductance et du condensateur.
Ici, $V_i(s)$ et $V_o(s)$ sont les transformées de Laplace de la tension d'entrée, $v_i(t)$ et tension de sortie, $v_o(t)$ respectivement.
le transfer function du réseau ci-dessus est
$$H(s) = \frac{V_o(s)}{V_i(s)} = \frac{sL + \frac{1}{sC}}{R + sL + \frac{1}{sC}}$$
$$\Rightarrow H(s) = \frac{s^2 LC + 1}{s^2 LC + sCR + 1}$$
Remplacer, $s = j \omega$ dans l'équation ci-dessus.
$$H(j \omega) = \frac{1 - \omega^2 LC}{1 - \omega^2 LC + j \omega CR}$$
L'ampleur de la fonction de transfert est
$$|H(j \omega)| = \frac{1 - \omega^2 LC}{\sqrt{(1 - \omega^2 LC)^2 + (\omega CR)^2}}$$
À ω = 0, la grandeur de la fonction de transfert est égale à 1.
À $\omega = \frac{1}{\sqrt{LC}}$, la grandeur de la fonction de transfert est égale à 0.
À ω = ∞, la grandeur de la fonction de transfert est égale à 1.
Par conséquent, l'ampleur de la fonction de transfert de Band stop filtervariera de 1 à 0 et de 0 à 1 car ω varie de 0 à ∞.