Théorie des réseaux - Théorème de Thevenin
Thevenin’s theoremindique que tout réseau ou circuit linéaire à deux bornes peut être représenté avec un réseau ou un circuit équivalent, qui consiste en une source de tension en série avec une résistance. Il est connu comme le circuit équivalent de Thevenin. Un circuit linéaire peut contenir des sources indépendantes, des sources dépendantes et des résistances.
Si le circuit contient plusieurs sources indépendantes, sources dépendantes et résistances, la réponse dans un élément peut être facilement trouvée en remplaçant l'ensemble du réseau à gauche de cet élément par un Thevenin’s equivalent circuit.
le response in an element peut être la tension à travers cet élément, le courant traversant cet élément ou la puissance dissipée à travers cet élément.
Ce concept est illustré dans les figures suivantes.
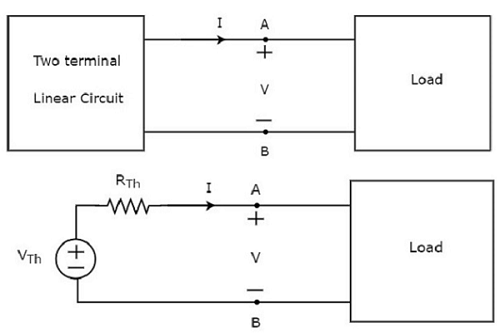
Thevenin’s equivalent circuitressemble à une source de tension pratique. Par conséquent, il a une source de tension en série avec une résistance.
La source de tension présente dans le circuit équivalent de Thevenin est appelée tension équivalente de Thevenin ou simplement Thevenin’s voltage, VTh.
La résistance présente dans le circuit équivalent de Thevenin est appelée résistance équivalente de Thevenin ou simplement Thevenin’s resistor, RTh.
Méthodes de recherche du circuit équivalent de Thevenin
Il existe trois méthodes pour trouver un circuit équivalent de Thevenin. Basé surtype of sourcesprésentes dans le réseau, nous pouvons choisir l'une de ces trois méthodes. Maintenant, laissez-nous discuter de deux méthodes une par une. Nous discuterons de la troisième méthode dans le chapitre suivant.
Méthode 1
Suivez ces étapes afin de trouver le circuit équivalent du Thevenin, lorsque seul le sources of independent type sont présents.
Step 1 - Considérez le schéma électrique en ouvrant les bornes par rapport auxquelles se trouve le circuit équivalent de Thevenin.
Step 2 - Trouvez la tension de Thevenin VTh aux bornes ouvertes du circuit ci-dessus.
Step 3 - Trouvez la résistance de Thevenin RTh aux bornes ouvertes du circuit ci-dessus en éliminant les sources indépendantes qui y sont présentes.
Step 4 - Dessinez le Thevenin’s equivalent circuiten connectant une tension de Thevenin V Th en série avec une résistance de Thevenin R Th .
Maintenant, nous pouvons trouver la réponse dans un élément qui se trouve sur le côté droit du circuit équivalent de Thevenin.
Exemple
Trouvez le courant traversant la résistance de 20 Ω en trouvant d'abord un Thevenin’s equivalent circuit à gauche des bornes A et B.
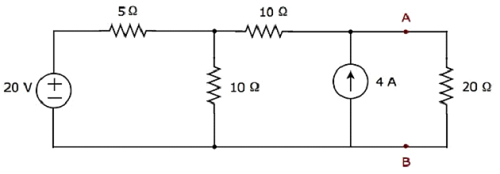
Step 1 - Afin de trouver le circuit équivalent de Thevenin sur le côté gauche des bornes A et B, nous devons retirer la résistance de 20 Ω du réseau en opening the terminals A & B. Le schéma de circuit modifié est illustré dans la figure suivante.
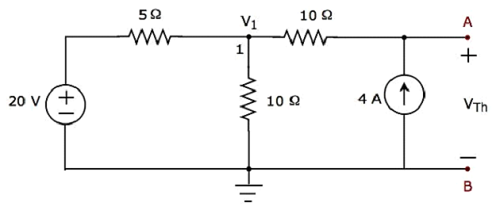
Step 2 - Calcul de Thevenin’s voltage VTh.
Il n'y a qu'un seul nœud principal sauf Ground dans le circuit ci-dessus. Donc, nous pouvons utilisernodal analysisméthode. La tension de nœud V 1 et la tension de Thevenin V Th sont indiquées dans la figure ci-dessus. Ici, V 1 est la tension du nœud 1 par rapport à la masse et V Th est la tension aux bornes de la source de courant 4 A.
le nodal equation au nœud 1 est
$$ \ frac {V_1 - 20} {5} + \ frac {V_1} {10} - 4 = 0 $$
$$ \ Rightarrow \ frac {2V_1 - 40 + V_1 - 40} {10} = 0 $$
$$ \ Rightarrow 3V_1 - 80 = 0 $$
$$ \ Rightarrow V_1 = \ frac {80} {3} V $$
La tension aux bornes de la résistance de la branche série 10 Ω est
$$ V_ {10 \ Omega} = (-4) (10) = -40V $$
Il y a deux mailles dans le circuit ci-dessus. leKVL equation autour du deuxième maillage est
$$ V_1 - V_ {10 \ Omega} - V_ {Th} = 0 $$
Remplacez les valeurs de $ V_1 $ et $ V_ {10 \ Omega} $ dans l'équation ci-dessus.
$$ \ frac {80} {3} - (-40) - V_ {Th} = 0 $$
$$ V_ {Th} = \ frac {80 + 120} {3} = \ frac {200} {3} V $$
Par conséquent, la tension de Thevenin est $ V_ {Th} = \ frac {200} {3} V $
Step 3 - Calcul de Thevenin’s resistance RTh.
Court-circuitez la source de tension et ouvrez la source de courant du circuit ci-dessus afin de calculer la résistance de Thevenin R Th aux bornes A et B.modified circuit diagram est illustré dans la figure suivante.
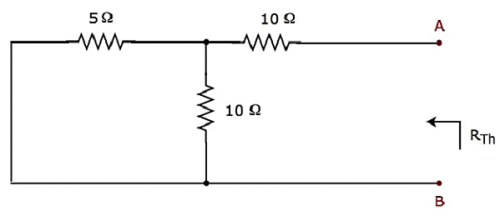
La résistance de Thevenin entre les bornes A et B sera
$$ R_ {Th} = \ lgroup \ frac {5 \ times 10} {5 + 10} \ rgroup + 10 = \ frac {10} {3} + 10 = \ frac {40} {3} \ Omega $$
Par conséquent, la résistance de Thevenin est $ \ mathbf {R_ {Th} = \ frac {40} {3} \ Omega} $.
Step 4- Le circuit équivalent de Thevenin est placé à gauche des bornes A et B dans le circuit donné. Ce schéma de circuit est illustré dans la figure suivante.

Le courant traversant la résistance de 20 Ω peut être trouvé en substituant les valeurs de V Th , R Th et R dans l'équation suivante.
$$ l = \ frac {V_ {Th}} {R_ {Th} + R} $$
$$ l = \ frac {\ frac {200} {3}} {\ frac {40} {3} + 20} = \ frac {200} {100} = 2A $$
Par conséquent, le courant traversant la résistance de 20 Ω est 2 A.
Méthode 2
Suivez ces étapes afin de trouver le circuit équivalent du Thevenin, lorsque le sources of both independent type and dependent type sont présents.
Step 1 - Considérez le schéma électrique en ouvrant les bornes par rapport auxquelles se trouve le circuit équivalent de Thevenin.
Step 2 - Trouvez la tension de Thevenin VTh aux bornes ouvertes du circuit ci-dessus.
Step 3 - Trouver le courant de court-circuit ISC en court-circuitant les deux bornes ouvertes du circuit ci-dessus.
Step 4 - Trouvez la résistance de Thevenin RTh en utilisant la formule suivante.
$$ R_ {Th} = \ frac {V_ {Th}} {I_ {SC}} $$
Step 5 - Dessinez le Thevenin’s equivalent circuiten connectant une tension de Thevenin V Th en série avec une résistance de Thevenin R Th .
Maintenant, nous pouvons trouver la réponse dans un élément qui se trouve sur le côté droit du circuit équivalent de Thevenin.