Théorie des réseaux - Analyse nodale
Il existe deux méthodes de base utilisées pour résoudre tout réseau électrique: Nodal analysis et Mesh analysis. Dans ce chapitre, parlons de laNodal analysis méthode.
Dans l'analyse nodale, nous considérerons les tensions des nœuds par rapport à la terre. Par conséquent, l'analyse nodale est également appeléeNode-voltage method.
Procédure d'analyse nodale
Suivez ces étapes lors de la résolution de tout réseau ou circuit électrique à l'aide de l'analyse nodale.
Step 1 - Identifier le principal nodes et choisissez l'un d'entre eux comme reference node. Nous traiterons ce nœud de référence comme le sol.
Step 2 - Étiqueter le node voltages par rapport à Ground à partir de tous les nœuds principaux sauf le nœud de référence.
Step 3 - Ecrire nodal equationsà tous les nœuds principaux à l'exception du nœud de référence. L'équation nodale est obtenue en appliquant d'abord KCL, puis la loi d'Ohm.
Step 4 - Résolvez les équations nodales obtenues à l'étape 3 afin d'obtenir les tensions des nœuds.
Maintenant, nous pouvons trouver le courant traversant n'importe quel élément et la tension à travers n'importe quel élément présent dans le réseau donné en utilisant les tensions de nœud.
Exemple
Trouvez le courant traversant la résistance de 20 Ω du circuit suivant en utilisant Nodal analysis.
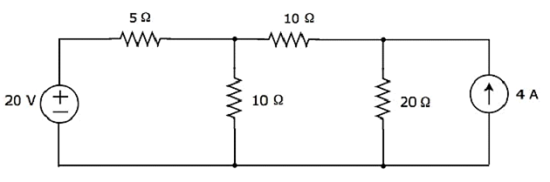
Step 1 - Il y a three principle nodesdans le circuit ci-dessus. Ceux-ci sont étiquetés comme 1, 2 et 3 dans la figure suivante.
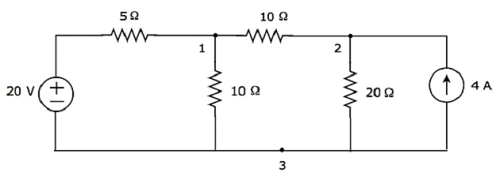
Dans la figure ci-dessus, considérez node 3 comme nœud de référence (Ground).
Step 2- Les tensions aux nœuds, V 1 et V 2 , sont indiquées dans la figure suivante.
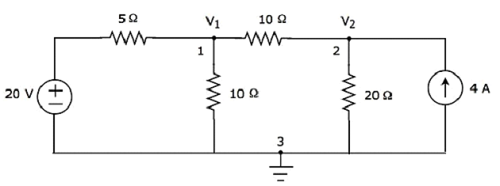
Sur la figure ci-dessus, V 1 est la tension du noeud 1 par rapport à la terre et V 2 est la tension du noeud 2 par rapport à la terre.
Step 3 - Dans ce cas, nous obtiendrons two nodal equations, car il y a deux nœuds principaux, 1 et 2, autres que Ground. Lorsque nous écrivons les équations nodales à un nœud, supposons que tous les courants partent du nœud pour lequel le sens du courant n'est pas mentionné et que la tension de ce nœud est supérieure aux autres tensions de nœud dans le circuit.
le nodal equation au nœud 1 est
$$ \ frac {V_1 - 20} {5} + \ frac {V_1} {10} + \ frac {V_1 - V_2} {10} = 0 $$
$$ \ Rightarrow \ frac {2 V_1 - 40 + V_1 + V_1 - V_2} {10} = 0 $$
$$ \ Flèche droite 4V_1 - 40 - V_2 = 0 $$
$ \ Rightarrow V_2 = 4V_1 - 40 $ Equation 1
le nodal equation au nœud 2 est
$$ - 4 + \ frac {V_2} {20} + \ frac {V_2 - V_1} {10} = 0 $$
$$ \ Rightarrow \ frac {-80 + V_2 + 2V_2 - 2V_2} {20} = 0 $$
$ \ Flèche droite 3V_2 - 2V_1 = 80 $ Equation 2
Step 4- Recherche des tensions de nœud, V 1 et V 2 en résolvant l'équation 1 et l'équation 2.
Remplacez l'équation 1 dans l'équation 2.
$$ 3 (4 V_1 - 40) - 2 V_1 = 80 $$
$$ \ Flèche droite 12 V_1 - 120 - 2V_1 = 80 $$
$$ \ Rightarrow 10 V_1 = 200 $$
$$ \ Flèche droite V_1 = 20V $$
Remplacez V 1 = 20 V dans l'équation 1.
$$ V_2 = 4 (20) - 40 $$
$$ \ Flèche droite V_2 = 40V $$
Donc, nous avons les tensions de nœud V 1 et V 2 comme20 V et 40 V respectivement.
Step 5- La tension aux bornes de la résistance de 20 Ω n'est rien d'autre que la tension du nœud V 2 et elle est égale à 40 V. Maintenant, nous pouvons trouver le courant traversant la résistance de 20 Ω en utilisant la loi d'Ohm.
$$ I_ {20 \ Omega} = \ frac {V_2} {R} $$
Remplacez les valeurs de V 2 et R dans l'équation ci-dessus.
$$ I_ {20 \ Omega} = \ frac {40} {20} $$
$$ \ Rightarrow I_ {20 \ Omega} = 2A $$
Par conséquent, le courant traversant la résistance de 20 Ω d'un circuit donné est 2 A.
Note- De l'exemple ci-dessus, nous pouvons conclure que nous devons résoudre 'n' équations nodales, si le circuit électrique a 'n' nœuds principaux (sauf le nœud de référence). Par conséquent, nous pouvons choisir l'analyse nodale lorsque lenumber of principal nodes (sauf noeud de référence) est inférieur au nombre de mailles de tout circuit électrique.