Théorie des réseaux - Conversion étoile en triangle
Dans le chapitre précédent, nous avons discuté de la conversion d'un réseau delta en un réseau en étoile équivalent. Parlons maintenant de la conversion du réseau en étoile en un réseau delta équivalent. Cette conversion est appeléeStar to Delta Conversion.
Dans le chapitre précédent, nous avons obtenu le resistances of star network du réseau delta comme
$ R_A = \ frac {R_1 R_2} {R_1 + R_2 + R_3} $ Equation 1
$ R_B = \ frac {R_2 R_3} {R_1 + R_2 + R_3} $ Equation 2
$ R_C = \ frac {R_3 R_1} {R_1 + R_2 + R_3} $ Equation 3
Résistances du réseau Delta en termes de résistances du réseau en étoile
Manipulons les équations ci-dessus afin d'obtenir les résistances du réseau delta en termes de résistances du réseau en étoile.
Multiply chaque ensemble de deux équations, puis add.
$$ R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 ^ 2 R_3 + R_2 R_3 ^ 2 R_1 + R_3 R_1 ^ 2 R_2} {(R_1 + R_2 + R_3) ^ 2} $$
$$ \ Rightarrow R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 R_3 (R_1 + R_2 + R_3)} {(R_1 + R_2 + R_3) ^ 2} $$
$ \ Rightarrow R_A R_B + R_B R_C + R_C R_A = \ frac {R_1 R_2 R_3} {R_1 + R_2 + R_3} $ Equation 4
En divisant l'équation 4 par l'équation 2, nous obtiendrons
$$ \ frac {R_A R_B + R_B R_C + R_C R_A} {R_B} = R_1 $$
$$ \ Rightarrow R_1 = R_C + R_A + \ frac {R_C R_A} {R_B} $$
En divisant l'équation 4 par l'équation 3, nous obtiendrons
$$ R_2 = R_A + R_B + \ frac {R_A R_B} {R_C} $$
En divisant l'équation 4 par l'équation 1, nous obtiendrons
$$ R_3 = R_B + R_C + \ frac {R_B R_C} {R_A} $$
En utilisant les relations ci-dessus, nous pouvons trouver les résistances du réseau delta à partir des résistances du réseau en étoile. De cette façon, nous pouvons convertirstar network into delta network.
Exemple
Calculons le resistances of delta network, qui sont équivalents à celui du réseau en étoile comme indiqué dans la figure suivante.
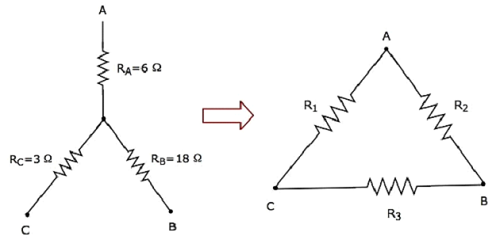
Compte tenu du resistances of star networkcomme R A = 6 Ω, R B = 18 Ω et R C = 3 Ω .
Nous connaissons les relations suivantes du resistances of delta network en termes de résistances de réseau en étoile.
$$ R_1 = R_C + R_A + \ frac {R_C R_A} {R_B} $$
$$ R_2 = R_A + R_B + \ frac {R_A R_B} {R_C} $$
$$ R_3 = R_B + R_C + \ frac {R_B R_C} {R_A} $$
Remplacez les valeurs de R A , R B et R C dans les équations ci-dessus.
$$ R_1 = 3 + 6 + \ frac {3 \ fois 6} {18} = 9 + 1 = 10 \ Omega $$
$$ R_2 = 6 + 18 + \ frac {6 \ fois 18} {3} = 24 + 36 = 60 \ Omega $$
$$ R_3 = 18 + 3 + \ frac {18 \ fois 3} {6} = 21 + 9 = 30 \ Omega $$
Donc, nous avons les résistances du réseau delta comme R1 = 10 Ω, R2 = 60 Ω et R3 = 30 Ω, qui sont équivalentes aux résistances du réseau en étoile donné.