Théorie des réseaux - Réponse des circuits CC
Si la sortie d'un circuit électrique pour une entrée varie en fonction du temps, alors elle est appelée comme time response. La réponse temporelle comprend les deux parties suivantes.
- Réponse transitoire
- Réponse en régime permanent
Dans ce chapitre, discutons d'abord de ces deux réponses, puis observons ces deux réponses dans un circuit série RL, lorsqu'il est excité par une source de tension continue.
Réponse transitoire
Après avoir appliqué une entrée à un circuit électrique, la sortie prend un certain temps pour atteindre un état stable. Ainsi, la sortie sera dans un état transitoire jusqu'à ce qu'elle passe à un état stable. Par conséquent, la réponse du circuit électrique pendant l'état transitoire est connue sous le nom detransient response.
La réponse transitoire sera nulle pour les grandes valeurs de «t». Idéalement, cette valeur de «t» devrait être l'infini. Mais, pratiquementfive time constants suffisent.
Présence ou absence de transitoires
Des transitoires se produisent dans la réponse en raison de sudden changedans les sources qui sont appliquées au circuit électrique et / ou en raison de l'action de commutation. Il existe deux actions de commutation possibles. Ce sont l'interrupteur d'ouverture et l'interrupteur de fermeture.
le transient une partie sera not presenten réponse à un circuit ou réseau électrique, s'il ne contient que des résistances. Carresistor a la capacité d'ajuster n'importe quelle quantité de tension et de courant.
le transient part occurs en réponse à un circuit ou réseau électrique en raison de la présence d'éléments de stockage d'énergie tels que inductor and capacitor. Parce qu'ils ne peuvent pas changer instantanément l'énergie stockée dans ces éléments.
Comportement de l'inducteur
Supposons que l'action de commutation a lieu à t = 0.Inductor currentne change pas instantanément, lorsque l'action de commutation a lieu. Cela signifie que la valeur du courant d'inductance juste après l'action de commutation sera la même que celle juste avant l'action de commutation.
Mathématiquement, il peut être représenté comme
$$ i_L (0 ^ +) = i_L (0 ^ -) $$
Comportement du condensateur
le capacitor voltagene change pas instantanément de la même manière que le courant de l'inducteur, lorsque l'action de commutation a lieu. Cela signifie que la valeur de la tension du condensateur juste après l'action de commutation sera la même que celle juste avant l'action de commutation.
Mathématiquement, il peut être représenté comme
$$ v_c (0 ^ +) = v_c (0 ^ -) $$
Réponse en régime permanent
La partie de la réponse temporelle qui reste même après que la réponse transitoire est devenue une valeur nulle pour les grandes valeurs de `` t '' est appelée steady state response. Cela signifie qu'il n'y aura pas de partie transitoire dans la réponse en régime permanent.
Comportement de l'inducteur
Si la source indépendante est connectée au circuit électrique ou au réseau ayant une ou plusieurs inductances et résistances (facultatives) pendant une longue période, alors ce circuit ou réseau électrique est dit en régime permanent. Par conséquent, l'énergie stockée dans le ou les inducteurs de ce circuit électrique est maximale et constante.
Mathématiquement, il peut être représenté comme
$ W_L = \ frac {L {i_L} ^ 2} {2} = $ Maximum & constant
$ \ Rightarrow i_L = $ Maximum & constant
Par conséquent, l'inducteur agit comme un constant current source en état d'équilibre.
La tension aux bornes de l'inducteur sera
$$ V_L = L \ frac {di_ {L}} {dt} = 0V $$
Ainsi, l'inducteur agit comme un short circuit en état d'équilibre.
Comportement du condensateur
Si la source indépendante est connectée au circuit électrique ou au réseau ayant un ou plusieurs condensateurs et résistances (facultatifs) pendant une longue période, alors ce circuit ou réseau électrique est dit en état stationnaire. Par conséquent, l'énergie stockée dans le ou les condensateurs de ce circuit électrique est maximale et constante.
Mathématiquement, il peut être représenté comme
$ W_c = \ frac {C {v_c} ^ 2} {2} = $ Maximum & constant
$ \ Rightarrow v_c = $ Maximum & constant
Par conséquent, le condensateur agit comme un constant voltage source en état d'équilibre.
Le courant traversant le condensateur sera
$$ i_c = C \ frac {dv_c} {dt} = 0A $$
Ainsi, le condensateur agit comme un open circuit en état d'équilibre.
Recherche de la réponse du circuit série RL
Considérer ce qui suit series RL circuit diagramme.
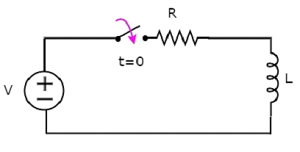
Dans le circuit ci-dessus, le switch était gardé openjusqu'à t = 0 et il était fermé à t = 0. Ainsi, la source de tension continue ayant V volts n'est pas connectée au circuit série RL jusqu'à cet instant. Par conséquent, il y ano initial current traverse l'inducteur.
Le schéma de circuit, lorsque le switch est dans closed la position est indiquée dans la figure suivante.
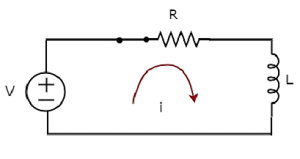
Maintenant, le courant i circule dans tout le circuit, la source de tension continue ayant V volts est connecté au circuit série RL.
Maintenant, postulez KVL autour de la boucle.
$$ V = Ri + L \ frac {di} {dt} $$
$ \ frac {di} {dt} + \ lgroup \ frac {R} {L} \ rgroup i = \ frac {V} {L} $Equation 1
L'équation ci-dessus est une équation différentielle du premier ordre et se présente sous la forme de
$ \ frac {dy} {dt} + Py = Q $Equation 2
Par comparing Équation 1 et équation 2, nous obtiendrons les relations suivantes.
$$ x = t $$
$$ y = i $$
$$ P = \ frac {R} {L} $$
$$ Q = \ frac {V} {L} $$
le solution de l'équation 2 sera
$ ye ^ {\ int p dx} = \ int Q e ^ {\ int p dx} dx + k $Equation 3
Où, k est la constante.
Remplacez, les valeurs de x, y, P & Q dans l'équation 3.
$ ie ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} = \ int (\ frac {V} {L}) \ lgroup e ^ {\ int {\ lgroup \ frac {R} {L} \ rgroup} dt} \ rgroup dt + k $
$ \ Rightarrow ie ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ int e ^ {\ lgroup \ frac {R} {L} \ rgroup t} dt + k $
$ \ Rightarrow ie ^ {\ lgroup \ frac {R} {L} \ rgroup t} = \ frac {V} {L} \ lbrace \ frac {e ^ {\ lgroup \ frac {R} {L} \ rgroup} t} {\ frac {R} {L}} \ rbrace + k $
$ \ Rightarrow i = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup} t $Equation 4
Nous savons qu'il n'y a pas de courant initial dans le circuit. Par conséquent, remplacez, t = 0 et = 0 dans l'équation 4 afin de trouver la valeur de la constante k.
$$ 0 = \ frac {V} {R} + ke ^ {- \ lgroup \ frac {R} {L} \ rgroup (0)} $$
$$ 0 = \ frac {V} {R} + k (1) $$
$$ k = - \ frac {V} {R} $$
Remplacez, la valeur de k dans l'équation 4.
$$ i = \ frac {V} {R} + \ lgroup - \ frac {V} {R} \ rgroup e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$
$$ i = \ frac {V} {R} - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $$
Par conséquent, la current circulant dans le circuit est
$ i = - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} + \ frac {V} {R} $Equation 5
Ainsi, la réponse du circuit série RL, lorsqu'il est excité par une source de tension continue, a les deux termes suivants.
Le premier terme $ - \ frac {V} {R} e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} $ correspond au transient response.
Le second terme $ \ frac {V} {R} $ correspond au steady state response. Ces deux réponses sont illustrées dans la figure suivante.
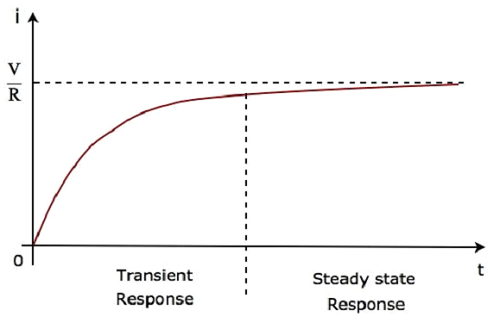
Nous pouvons réécrire l'équation 5 comme suit -
$ i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {R} {L} \ rgroup t} \ rgroup $
$ \ Rightarrow i = \ frac {V} {R} \ lgroup 1 - e ^ {- \ lgroup \ frac {t} {\ tau} \ rgroup} \ rgroup $Equation 6
Où, τ est le time constant et sa valeur est égale à $ \ frac {L} {R} $.
L'équation 5 et l'équation 6 sont identiques. Mais, nous pouvons facilement comprendre la forme d'onde ci-dessus du courant circulant dans le circuit à partir de l'équation 6 en substituant quelques valeurs det comme 0, τ, 2τ, 5τ, etc.
Dans la forme d'onde ci-dessus du courant circulant dans le circuit, la réponse transitoire présentera jusqu'à cinq constantes de temps à partir de zéro, tandis que la réponse en régime permanent présentera à partir de cinq constantes de temps.