Théorie des réseaux - Analyse du maillage
Dans l'analyse de maillage, nous considérerons les courants circulant à travers chaque maillage. Par conséquent, l'analyse de maillage est également appeléeMesh-current method.
UNE branchest un chemin qui relie deux nœuds et contient un élément de circuit. Si une branche appartient à un seul maillage, alors le courant de branche sera égal au courant de maillage.
Si une branche est commune à deux mailles, alors le courant de branche sera égal à la somme (ou à la différence) de deux courants de maillage, lorsqu'ils sont dans le même sens (ou dans le sens opposé).
Procédure d'analyse du maillage
Suivez ces étapes lors de la résolution de tout réseau ou circuit électrique à l'aide de l'analyse de maillage.
Step 1 - Identifier le meshes et étiquetez les courants de maillage dans le sens horaire ou anti-horaire.
Step 2 - Observez la quantité de courant qui traverse chaque élément en termes de courants de maillage.
Step 3 - Ecrire mesh equationsà tous les maillages. L'équation de maillage est obtenue en appliquant d'abord KVL puis la loi d'Ohm.
Step 4 - Résoudre les équations de maillage obtenues à l'étape 3 afin d'obtenir le mesh currents.
Maintenant, nous pouvons trouver le courant traversant n'importe quel élément et la tension à travers n'importe quel élément présent dans le réseau donné en utilisant des courants de maillage.
Exemple
Trouvez la tension aux bornes de la résistance de 30 Ω en utilisant Mesh analysis.
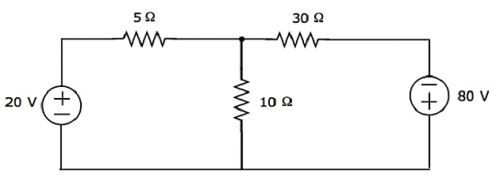
Step 1- Il y a deux mailles dans le circuit ci-dessus. lemesh currentsI 1 et I 2 sont considérés dans le sens des aiguilles d'une montre. Ces courants de maillage sont illustrés dans la figure suivante.
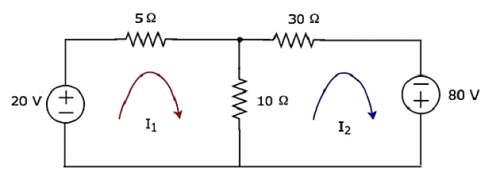
Step 2- Le courant de maillage I 1 traverse une source de tension de 20 V et une résistance de 5 Ω. De même, le courant de maillage I 2 circule à travers une résistance de 30 Ω et une source de tension -80 V. Mais, la différence de deux courants de maillage, I 1 et I 2 , traverse une résistance de 10 Ω, car il s'agit de la branche commune de deux mailles.
Step 3 - Dans ce cas, nous obtiendrons two mesh equationscar il y a deux mailles dans le circuit donné. Lorsque nous écrivons les équations de maillage, supposons que le courant de maillage de ce maillage particulier est supérieur à tous les autres courants de maillage du circuit.
le mesh equation du premier maillage est
$$ 20 - 5I_1 -10 (I_1 - I_2) = 0 $$
$$ \ Flèche droite 20 - 15I_1 + 10I_2 = 0 $$
$$ \ Rightarrow 10I_2 = 15I_1 - 20 $$
Divisez l'équation ci-dessus par 5.
$$ 2I_2 = 3I_1 - 4 $$
Multipliez l'équation ci-dessus par 2.
$ 4I_2 = 6I_1 - 8 $ Equation 1
le mesh equation du deuxième maillage est
$$ - 10 (I_2 - I_1) - 30I_2 + 80 = 0 $$
Divisez l'équation ci-dessus par 10.
$$ - (I_2 - I_1) - 3I_2 + 8 = 0 $$
$$ \ Flèche droite -4I_2 + I_1 + 8 = 0 $$
$ 4I_2 = I_1 + 8 $ Equation 2
Step 4- Trouver les courants de maillage I 1 et I 2 en résolvant l'équation 1 et l'équation 2.
Les termes de gauche de l'équation 1 et de l'équation 2 sont les mêmes. Par conséquent, assimilez les termes de droite de l'équation 1 et de l'équation 2 afin de trouver la valeur de I 1 .
$$ 6I_1 - 8 = I_1 + 8 $$
$$ \ Rightarrow 5I_1 = 16 $$
$$ \ Rightarrow I_1 = \ frac {16} {5} A $$
Remplacez la valeur I 1 dans l'équation 2.
$$ 4I_2 = \ frac {16} {5} + 8 $$
$$ \ Rightarrow 4I_2 = \ frac {56} {5} $$
$$ \ Rightarrow I_2 = \ frac {14} {5} A $$
Donc, nous avons obtenu les courants de maillage I 1 et I 2 comme $ \ mathbf {\ frac {16} {5}} $A et $ \ mathbf {\ frac {14} {5}} $ A respectivement.
Step 5- Le courant traversant la résistance 30 Ω n'est rien d'autre que le courant de maillage I 2 et il est égal à $ \ frac {14} {5} $ A. Maintenant, nous pouvons trouver la tension à travers la résistance 30 Ω en utilisant la loi d'Ohm.
$$ V_ {30 \ Omega} = I_2 R $$
Remplacez les valeurs de I 2 et R dans l'équation ci-dessus.
$$ V_ {30 \ Omega} = \ lgroup \ frac {14} {5} \ rgroup 30 $$
$$ \ Rightarrow V_ {30 \ Omega} = 84V $$
Par conséquent, la tension aux bornes de la résistance de 30 Ω du circuit donné est 84 V.
Note 1- A partir de l'exemple ci-dessus, nous pouvons conclure que nous devons résoudre les équations de maillage 'm', si le circuit électrique a des mailles 'm'. C'est pourquoi on peut choisir l'analyse de maillage lorsque le nombre de mailles est inférieur au nombre de nœuds principaux (sauf le nœud de référence) de n'importe quel circuit électrique.
Note 2 - On peut choisir soit l'analyse nodale, soit l'analyse de maillage, lorsque le nombre de mailles est égal au nombre de nœuds principaux (sauf le nœud de référence) dans n'importe quel circuit électrique.