Théorie des réseaux - Théorème de superposition
Superposition theoremest basé sur le concept de linéarité entre la réponse et l'excitation d'un circuit électrique. Il déclare que la réponse dans une branche particulière d'un circuit linéaire lorsque plusieurs sources indépendantes agissent en même temps est équivalente à la somme des réponses dues à chaque source indépendante agissant à la fois.
Dans cette méthode, nous ne considérerons que one independent sourceà la fois. Nous devons donc éliminer les sources indépendantes restantes du circuit. On peut éliminer les sources de tension en court-circuitant leurs deux bornes et de même, les sources de courant en ouvrant leurs deux bornes.
Par conséquent, nous devons trouver la réponse dans une branche particulière ‘n’ timess'il y a 'n' sources indépendantes. La réponse dans une branche particulière peut être soit un courant circulant dans cette branche, soit une tension à travers cette branche.
Procédure du théorème de superposition
Suivez ces étapes afin de trouver la réponse dans une branche particulière en utilisant le théorème de superposition.
Step 1 - Trouvez la réponse dans une branche particulière en considérant une source indépendante et en éliminant les sources indépendantes restantes présentes dans le réseau.
Step 2 - Répétez l'étape 1 pour toutes les sources indépendantes présentes sur le réseau.
Step 3 - Ajouter toutes les réponses afin d'obtenir la réponse globale dans une branche particulière lorsque toutes les sources indépendantes sont présentes dans le réseau.
Exemple
Trouvez le courant traversant la résistance de 20 Ω du circuit suivant en utilisant superposition theorem.
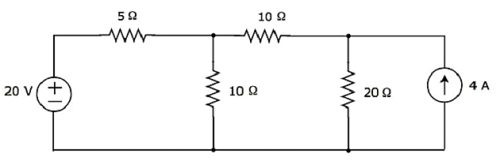
Step 1 - Trouvons le courant traversant la résistance de 20 Ω en considérant uniquement 20 V voltage source. Dans ce cas, on peut éliminer la source de courant 4 A en en faisant un circuit ouvert. Le schéma de circuit modifié est illustré dans la figure suivante.

Il n'y a qu'un seul nœud principal sauf Ground dans le circuit ci-dessus. Donc, nous pouvons utilisernodal analysisméthode. La tension de nœud V 1 est indiquée dans la figure suivante. Ici, V 1 est la tension du nœud 1 par rapport à la masse.
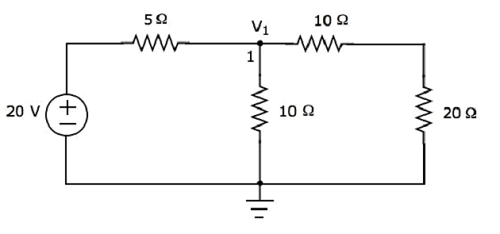
le nodal equation au nœud 1 est
$$ \ frac {V_1 - 20} {5} + \ frac {V_1} {10} + \ frac {V_1} {10 + 20} = 0 $$
$$ \ Rightarrow \ frac {6V_1 - 120 + 3V_1 + V_1} {30} = 0 $$
$$ \ Rightarrow 10V_1 = 120 $$
$$ \ Rightarrow V_1 = 12 V $$
le current flowing through 20 Ω resistor peut être trouvée en faisant la simplification suivante.
$$ I_1 = \ frac {V_1} {10 + 20} $$
Remplacez la valeur de V 1 dans l'équation ci-dessus.
$$ I_1 = \ frac {12} {10 + 20} = \ frac {12} {30} = 0,4 A $$
Par conséquent, le courant traversant la résistance de 20 Ω est 0.4 A, lorsque seule une source de tension de 20 V est prise en compte.
Step 2 - Trouvons le courant traversant la résistance de 20 Ω en considérant uniquement 4 A current source. Dans ce cas, on peut éliminer la source de tension 20 V en la faisant en court-circuit. Le schéma de circuit modifié est illustré dans la figure suivante.
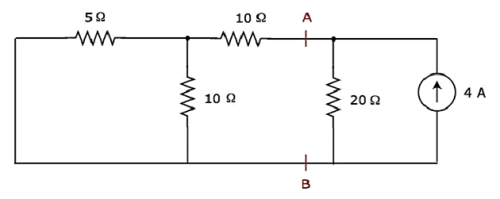
Dans le circuit ci-dessus, il y a trois résistances à gauche des bornes A et B.Nous pouvons remplacer ces résistances par une seule equivalent resistor. Ici, les résistances 5 Ω et 10 Ω sont connectées en parallèle et toute la combinaison est en série avec une résistance de 10 Ω.
le equivalent resistance à gauche des terminaux A et B sera
$$ R_ {AB} = \ lgroup \ frac {5 \ times 10} {5 + 10} \ rgroup + 10 = \ frac {10} {3} + 10 = \ frac {40} {3} \ Omega $$
Le schéma de circuit simplifié est illustré dans la figure suivante.
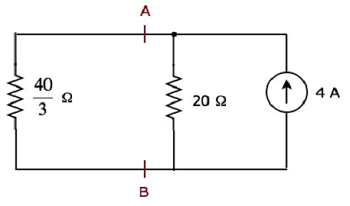
Nous pouvons trouver le courant traversant la résistance de 20 Ω, en utilisant current division principle.
$$ I_2 = I_S \ lgroup \ frac {R_1} {R_1 + R_2} \ rgroup $$
Remplacez $ I_S = 4A, \: R_1 = \ frac {40} {3} \ Omega $ et $ R_2 = 20 \ Omega $ dans l'équation ci-dessus.
$$ I_2 = 4 \ lgroup \ frac {\ frac {40} {3}} {\ frac {40} {3} + 20} \ rgroup = 4 \ lgroup \ frac {40} {100} \ rgroup = 1,6 A $$
Par conséquent, le courant traversant la résistance de 20 Ω est 1.6 A, lorsque seulement une source de courant de 4 A est prise en compte.
Step 3 - Nous obtiendrons le courant traversant la résistance de 20 Ω du circuit donné en faisant le addition of two currents que nous avons obtenu aux étapes 1 et 2. Mathématiquement, il peut s'écrire
$$ I = I_1 + I_2 $$
Remplacez par les valeurs de I 1 et I 2 dans l'équation ci-dessus.
$$ I = 0,4 + 1,6 = 2 A $$
Par conséquent, le courant traversant la résistance de 20 Ω d'un circuit donné est 2 A.
Note - On ne peut pas appliquer directement le théorème de superposition pour trouver la quantité de powerlivré à toute résistance présente dans un circuit linéaire, simplement en ajoutant les puissances délivrées à cette résistance en raison de chaque source indépendante. Au contraire, nous pouvons calculer soit le courant total traversant ou la tension à travers cette résistance en utilisant le théorème de superposition et à partir de cela, nous pouvons calculer la quantité de puissance fournie à cette résistance en utilisant $ I ^ 2 R $ ou $ \ frac {V ^ 2} {R} $.