Théorie des réseaux - Résonance parallèle
Dans le chapitre précédent, nous avons discuté de l'importance de la résonance des séries. Parlons maintenant de la résonance parallèle dans les circuits RLC.
Schéma du circuit de résonance parallèle
Si la résonance se produit dans un circuit RLC parallèle, elle est appelée Parallel Resonance. Considérer ce qui suitparallel RLC circuit, qui est représenté dans le domaine du phaseur.
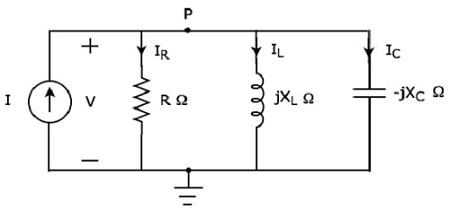
Ici, les éléments passifs tels que la résistance, l'inductance et le condensateur sont connectés en parallèle. Toute cette combinaison est enparallel avec la source de courant sinusoïdale d'entrée.
Écrire nodal equation au nœud P.
$$ - I + I_R + I_L + I_C = 0 $$
$$ \ Rightarrow - I + \ frac {V} {R} + \ frac {V} {j X_L} + \ frac {V} {- j X_C} = 0 $$
$$ \ Rightarrow I = \ frac {V} {R} - \ frac {jV} {X_L} + \ frac {jV} {X_C} $$
$ \ Rightarrow I = V [\ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup] $Equation 1
L'équation ci-dessus se présente sous la forme de I = VY.
Par conséquent, la admittance Y du circuit RLC parallèle sera
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup $$
Paramètres et grandeurs électriques à la résonance
Maintenant, dérivons les valeurs des paramètres et des grandeurs électriques à la résonance du circuit RLC parallèle une par une.
Fréquence de résonance
Nous savons que le resonant frequency, frest la fréquence à laquelle la résonance se produit. Dans le circuit RLC parallèle, la résonance se produit, lorsque le terme imaginaire d'admittance, Y est nul. c'est-à-dire que la valeur de $ \ frac {1} {X_C} - \ frac {1} {X_L} $ doit être égale à zéro
$$ \ Rightarrow \ frac {1} {X_C} = \ frac {1} {X_L} $$
$$ \ Rightarrow X_L = X_C $$
La condition de résonance ci-dessus est la même que celle du circuit RLC série. Alors leresonant frequency, fr sera le même dans le circuit RLC série et le circuit RLC parallèle.
Par conséquent, la resonant frequency, fr du circuit RLC parallèle est
$$ f_r = \ frac {1} {2 \ pi \ sqrt {LC}} $$
Où,
- L est l'inductance d'un inducteur.
- C est la capacité d'un condensateur.
le resonant frequency, fr du circuit RLC parallèle ne dépend que de l'inductance L et capacité C. Mais, c'est indépendant de la résistanceR.
Admission
Nous avons le admittance Y du circuit RLC parallèle comme
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_L} \ rgroup $$
Remplacez, $ X_L = X_C $ dans l'équation ci-dessus.
$$ Y = \ frac {1} {R} + j \ lgroup \ frac {1} {X_C} - \ frac {1} {X_C} \ rgroup $$
$$ \ Rightarrow Y = \ frac {1} {R} + j (0) $$
$$ \ Rightarrow Y = \ frac {1} {R} $$
À la résonance, le admittance, Y du circuit RLC parallèle est égal à l'inverse de la résistance, R. ie, $ \ mathbf {\ mathit {Y = \ frac {1} {R}}} $
Tension à travers chaque élément
Substitut, $ \ frac {1} {X_C} - \ frac {1} {X_L} = 0 $ dans l'équation 1
$$ I = V [\ frac {1} {R} + j (0)] $$
$$ \ Rightarrow I = \ frac {V} {R} $$
$$ \ Rightarrow V = IR $$
Par conséquent, la voltage à travers tous les éléments du circuit RLC parallèle à la résonance est V = IR.
À la résonance, l'admittance du circuit RLC parallèle atteint la valeur minimale. Par conséquent,maximum voltage est présent à travers chaque élément de ce circuit à la résonance.
Courant traversant la résistance
Le courant traversant la résistance est
$$ I_R = \ frac {V} {R} $$
Remplacez la valeur de V dans l'équation ci-dessus.
$$ I_R = \ frac {IR} {R} $$
$$ \ Rightarrow I_R = I $$
Par conséquent, la current flowing through resistor à la résonance est $ \ mathbf {\ mathit {I_R = I}} $.
Courant circulant à travers l'inducteur
Le courant traversant l'inducteur est
$$ I_L = \ frac {V} {j X_L} $$
Remplacez la valeur de V dans l'équation ci-dessus.
$$ I_L = \ frac {IR} {j X_L} $$
$$ \ Rightarrow I_L = -j \ lgroup \ frac {R} {X_L} \ rgroup I $$
$$ \ Rightarrow I_L = -jQI $$
Par conséquent, la current flowing through inductor à la résonance est $ I_L = -jQI $.
Alors le magnitude du courant traversant l'inducteur à la résonance sera
$$ | I_L | = QI $$
Où, Q est le Quality factor et sa valeur est égale à $ \ frac {R} {X_L} $
Courant traversant le condensateur
Le courant traversant le condensateur est
$$ I_C = \ frac {V} {- j X_C} $$
Remplacez la valeur de V dans l'équation ci-dessus.
$$ I_C = \ frac {IR} {- j X_C} $$
$$ \ Rightarrow I_C = j \ lgroup \ frac {R} {X_C} \ rgroup I $$
$$ \ Rightarrow I_C = jQI $$
Par conséquent, la current flowing through capacitor à la résonance est $ I_C = jQI $
Alors le magnitude du courant traversant le condensateur à la résonance sera
$$ | I_C | = QI $$
Où, Q est le Quality factor et sa valeur est égale à $ \ frac {R} {X_C} $
Note - Le circuit RLC à résonance parallèle est appelé current magnificationcircuit. Parce que l'amplitude du courant circulant à travers l' inductance et le condensateur est égale à Q fois l'entrée sinusoïdale de courant I .