Théorie des réseaux - Résonance des séries
Resonancese produit dans les circuits électriques en raison de la présence d'éléments de stockage d'énergie comme l'inductance et le condensateur. C'est le concept fondamental sur lequel les récepteurs de radio et de télévision sont conçus de manière à ne pouvoir sélectionner que la fréquence de la station souhaitée.
Il y a two typesde résonances, à savoir résonance série et résonance parallèle. Ceux-ci sont classés en fonction des éléments du réseau connectés en série ou en parallèle. Dans ce chapitre, parlons de la résonance des séries.
Schéma du circuit de résonance en série
Si la résonance se produit dans le circuit RLC série, elle est appelée Series Resonance. Considérer ce qui suitseries RLC circuit, qui est représenté dans le domaine du phaseur.
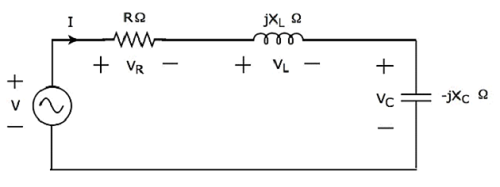
Ici, les éléments passifs tels que la résistance, l'inductance et le condensateur sont connectés en série. Toute cette combinaison est enseries avec la source de tension sinusoïdale d'entrée.
Appliquer KVL autour de la boucle.
$$ V - V_R - V_L - V_C = 0 $$
$$ \ Flèche droite V - IR - I (j X_L) - I (-j X_C) = 0 $$
$$ \ Flèche droite V = IR + I (j X_L) + I (-j X_C) $$
$ \ Flèche droite V = I [R + j (X_L - X_C)] $Equation 1
L'équation ci-dessus se présente sous la forme de V = IZ.
Par conséquent, la impedance Z du circuit RLC série sera
$$ Z = R + j (X_L - X_C) $$
Paramètres et grandeurs électriques à la résonance
Maintenant, dérivons les valeurs des paramètres et des grandeurs électriques à la résonance du circuit série RLC une par une.
Fréquence de résonance
La fréquence à laquelle la résonance se produit est appelée resonant frequency fr. En série, la résonance du circuit RLC se produit, lorsque le terme imaginaire de l'impédance Z est nul, c'est-à-dire que la valeur de $ X_L - X_C $ doit être égale à zéro.
$$ \ Rightarrow X_L = X_C $$
Remplacez $ X_L = 2 \ pi f L $ et $ X_C = \ frac {1} {2 \ pi f C} $ dans l'équation ci-dessus.
$$ 2 \ pi f L = \ frac {1} {2 \ pi f C} $$
$$ \ Rightarrow f ^ 2 = \ frac {1} {(2 \ pi) ^ 2 LC} $$
$$ \ Rightarrow f = \ frac {1} {(2 \ pi) \ sqrt {LC}} $$
Par conséquent, la resonant frequency fr du circuit RLC série est
$$ f_r = \ frac {1} {(2 \ pi) \ sqrt {LC}} $$
Où, L est l'inductance d'un inducteur et C est la capacité d'un condensateur.
le resonant frequency fr du circuit RLC série ne dépend que de l'inductance L et capacité C. Mais, c'est indépendant de la résistanceR.
Impédance
Nous avons le impedance Z du circuit RLC série comme
$$ Z = R + j (X_L - X_C) $$
Remplacez $ X_L = X_C $ dans l'équation ci-dessus.
$$ Z = R + j (X_C - X_C) $$
$$ \ Flèche droite Z = R + j (0) $$
$$ \ Flèche droite Z = R $$
À la résonance, le impedance Z du circuit RLC série est égal à la valeur de la résistance R, c'est à dire, Z = R.
Courant circulant dans le circuit
Remplacez $ X_L - X_C = 0 $ dans l'équation 1.
$$ V = I [R + j (0)] $$
$$ \ Rightarrow V = IR $$
$$ \ Rightarrow I = \ frac {V} {R} $$
Par conséquent, current circulant à travers le circuit RLC série à la résonance est $ \ mathbf {\ mathit {I = \ frac {V} {R}}} $.
À la résonance, l'impédance du circuit RLC série atteint sa valeur minimale. D'où lemaximum current traverse ce circuit à la résonance.
Tension à travers la résistance
La tension aux bornes de la résistance est
$$ V_R = IR $$
Remplacez la valeur de I dans l'équation ci-dessus.
$$ V_R = \ lgroup \ frac {V} {R} \ rgroup R $$
$$ \ Flèche droite V_R = V $$
Par conséquent, la voltage across resistor à la résonance est VR = V.
Tension à travers l'inducteur
La tension aux bornes de l'inducteur est
$$ V_L = I (jX_L) $$
Remplacez la valeur de I dans l'équation ci-dessus.
$$ V_L = \ lgroup \ frac {V} {R} \ rgroup (jX_L) $$
$$ \ Rightarrow V_L = j \ lgroup \ frac {X_L} {R} \ rgroup V $$
$$ \ Rightarrow V_L = j QV $$
Par conséquent, la voltage across inductor à la résonance est $ V_L = j QV $.
Alors le magnitude de tension aux bornes de l'inductance à la résonance sera
$$ | V_L | = QV $$
Où Q est le Quality factor et sa valeur est égale à $ \ frac {X_L} {R} $
Tension à travers le condensateur
La tension aux bornes du condensateur est
$$ V_C = I (-j X_C) $$
Remplacez la valeur de I dans l'équation ci-dessus.
$$ V_C = \ lgroup \ frac {V} {R} \ rgroup (-j X_C) $$
$$ \ Rightarrow V_C = -j \ lgroup \ frac {X_C} {R} \ rgroup V $$
$$ \ Rightarrow V_C = -jQV $$
Par conséquent, la voltage across capacitor à la résonance est $ \ mathbf {\ mathit {V_C = -jQV}} $.
Alors le magnitude de tension aux bornes du condensateur à la résonance sera
$$ | V_C | = QV $$
Où Q est le Quality factor et sa valeur est égale à $ \ frac {X_ {C}} {R} $
Note - Le circuit RLC de résonance en série est appelé voltage magnificationcircuit, parce que l'amplitude de tension aux bornes de l'inductance et le condensateur est égale à Q fois la tension sinusoïdale d' entrée V .