アナログ通信-FM変調器
この章では、NBFM波とWBFM波を生成する変調器について説明します。まず、NBFMの生成について説明します。
NBFMの生成
FM波の標準方程式は次のとおりです。
$$ s \ left(t \ right)= A_c \ cos \ left(2 \ pi f_ct + 2 \ pi k_f \ int m \ left(t \ right)dt \ right)$$
$ \ Rightarrow s \ left(t \ right)= A_c \ cos \ left(2 \ pi f_ct \ right)\ cos \ left(2 \ pi k_f \ int m \ left(t \ right)dt \ right)-$
$ A_c \ sin \ left(2 \ pi f_ct \ right)\ sin \ left(2 \ pi k_f \ int m \ left(t \ right)dt \ right)$
NBFMの場合、
$$ \左| 2 \ pi k_f \ int m \ left(t \ right)dt \ right | << 1 $$
$ \ theta $が非常に小さい場合、$ \ cos \ theta \ upper x 1 $と$ \ sin \ theta \ upper x 1 $がわかります。
上記の関係を使用することにより、 NBFM equation なので
$$ s \ left(t \ right)= A_c \ cos \ left(2 \ pi f_ct \ right)-A_c \ sin \ left(2 \ pi f_ct \ right)2 \ pi k_f \ int m \ left(t \右)dt $$
NBFM変調器のブロック図を次の図に示します。
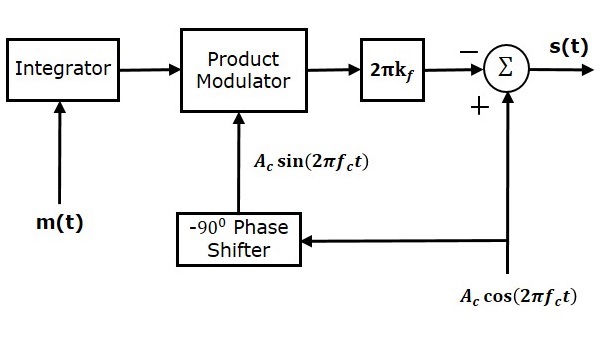
ここでは、積分器を使用して変調信号$ m \ left(t \ right)$を積分します。キャリア信号$ A_c \ cos \ left(2 \ pi f_ct \ right)$は、$ A_c \ sin \ left(2 \ pi f_ct \ right)$を取得するために$ -90 ^ 0 $だけ位相シフトされます。 $ -90 ^ 0 $移相器。積変調器には、2つの入力$ \ int m \ left(t \ right)dt $と$ A_c \ sin \ left(2 \ pi f_ct \ right)$があります。これら2つの入力の積である出力を生成します。
これは、フォワードパスにブロック$ 2 \ pi k_f $を配置することにより、$ 2 \ pi k_f $でさらに乗算されます。サマーブロックには2つの入力があり、これはNBFM方程式の2つの項に他なりません。正と負の符号は、サマーブロックの入力でキャリア信号と他の項に割り当てられます。最後に、夏のブロックはNBFM波を生成します。
WBFMの生成
次の2つの方法でWBFM波を生成します。
- 直接法
- 間接法
直接法
この方法は、広帯域FM波を直接生成するため、直接法と呼ばれます。この方法では、電圧制御発振器(VCO)を使用してWBFMを生成します。VCOは、周波数が入力信号電圧に比例する出力信号を生成します。これはFM波の定義に似ています。WBFM波の発生のブロック図を次の図に示します。

ここでは、変調信号$ m \ left(t \ right)$が電圧制御発振器(VCO)の入力として適用されます。VCOは、WBFMに他ならない出力を生成します。
$$ f_i \:\ alpha \:m \ left(t \ right)$$
$$ \ Rightarrow f_i = f_c + k_fm \ left(t \ right)$$
どこ、
$ f_i $は、WBFM波の瞬時周波数です。
間接法
この方法は、広帯域FM波を間接的に生成しているため、間接法と呼ばれます。つまり、最初にNBFM波を生成し、次に周波数逓倍器を使用してWBFM波を生成します。WBFM波の発生のブロック図を次の図に示します。

このブロック図には、主に2つの段階が含まれています。最初の段階では、NBFM変調器を使用してNBFM波が生成されます。この章の冒頭で、NBFM変調器のブロック図を見てきました。NBFM波の変調指数は1未満であることがわかっています。したがって、FM波に必要な変調指数(1より大きい)を取得するには、周波数逓倍器の値を適切に選択します。
Frequency multiplierは非線形デバイスであり、周波数が入力信号周波数の「n」倍である出力信号を生成します。ここで、「n」は乗算係数です。
変調指数$ \ beta $が1未満のNBFM波が周波数逓倍器の入力として適用される場合、周波数逓倍器は、変調指数が 'n'×$ \ beta $で、周波数も 'nである出力信号を生成します。 'WBFM波の周波数の倍。
FM波の周波数偏差と変調指数を上げるために、周波数逓倍器とミキサーの複数のステージが必要になる場合があります。