アナログ通信-SNR計算
この章では、受信機で復調されるさまざまな変調波の信号対雑音比と性能指数を計算しましょう。
信号対雑音比
Signal-to-Noise Ratio (SNR)は、信号電力とノイズ電力の比率です。SNRの値が高いほど、受信出力の品質が高くなります。
さまざまなポイントでの信号対雑音比は、次の式を使用して計算できます。
Input SNR = $ \ left(SNR \ right)_I = \ frac {Average \:\:power \:\:of \:\:modulating \:\:signal} {Average \:\:power \:\:of \: \:noise \:\:at \:\:input} $
Output SNR = $ \ left(SNR \ right)_O = \ frac {Average \:\:power \:\:of \:\:demodulated \:\:signal} {Average \:\:power \:\:of \: \:noise \:\:at \:\:output} $
Channel SNR = $ \ left(SNR \ right)_C = \ frac {Average \:\:power \:\:of \:\:modulated \:\:signal} {Average \:\:power \:\:of \: \:noise \:\:in \:\:message \:\:bandwidth} $
性能指数
出力SNRと入力SNRの比率は、次のように表すことができます。 Figure of Merit。それはによって示されますF。デバイスのパフォーマンスについて説明します。
$$ F = \ frac {\ left(SNR \ right)_O} {\ left(SNR \ right)_I} $$
受信機の性能指数は
$$ F = \ frac {\ left(SNR \ right)_O} {\ left(SNR \ right)_C} $$
これは、受信機の場合、チャネルが入力であるためです。
AMシステムでのSNR計算
ノイズを分析するために、AMシステムの次の受信機モデルを検討してください。

振幅変調(AM)波は
$$ s \ left(t \ right)= A_c \ left [1 + k_am \ left(t \ right)\ right] \ cos \ left(2 \ pi f_ct \ right)$$
$$ \ Rightarrow s \ left(t \ right)= A_c \ cos \ left(2 \ pi f_ct \ right)+ A_ck_am \ left(t \ right)\ cos \ left(2 \ pi f_ct \ right)$$
AM波の平均パワーは
$$ P_s = \ left(\ frac {A_c} {\ sqrt {2}} \ right)^ 2 + \ left(\ frac {A_ck_am \ left(t \ right)} {\ sqrt {2}} \ right) ^ 2 = \ frac {{A_ {c}} ^ {2}} {2} + \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2} $ $
$$ \ Rightarrow P_s = \ frac {{A_ {c}} ^ {2} \ left(1+ {k_ {a}} ^ {2} P \ right)} {2} $$
メッセージ帯域幅のノイズの平均パワーは
$$ P_ {nc} = WN_0 $$
代わりに、これらの値は channel SNR 式
$$ \ left(SNR \ right)_ {C、AM} = \ frac {Average \:\:Power \:\:of \:\:AM \:\:Wave} {Average \:\:Power \: \:of \:\:ノイズ\:\:in \:\:メッセージ\:\:帯域幅} $$
$$ \ Rightarrow \ left(SNR \ right)_ {C、AM} = \ frac {{A_ {c}} ^ {2} \ left(1+ {k_ {a}} ^ {2} \ right)P } {2WN_0} $$
どこ、
P メッセージ信号のパワーです= $ \ frac {{A_ {m}} ^ {2}} {2} $
W メッセージの帯域幅です
上図に示すように、バンドパスノイズがチャネル内のAM波と混合されていると仮定します。この組み合わせは、AM復調器の入力に適用されます。したがって、AM復調器の入力はです。
$$ v \ left(t \ right)= s \ left(t \ right)+ n \ left(t \ right)$$
$ \ Rightarrow v \ left(t \ right)= A_c \ left [1 + k_am \ left(t \ right)\ right] \ cos \ left(2 \ pi f_ct \ right)+ $
$ \ left [n_1 \ left(t \ right)\ cos \ left(2 \ pi f_ct \ right)-n_Q \ left(t \ right)\ sin \ left(2 \ pi f_ct \ right)\ right] $
$ \ Rightarrow v \ left(t \ right)= \ left [A_c + A_ck_am \ left(t \ right)+ n_1 \ left(t \ right)\ right] \ cos \ left(2 \ pi f_ct \ right)- n_Q \ left(t \ right)\ sin \ left(2 \ pi f_ct \ right)$
ここで、$ n_I \ left(t \ right)$と$ n_Q \ left(t \ right)$は、ノイズの同相成分と直交位相成分です。
AM復調器の出力は、上記の信号のエンベロープに他なりません。
$$ d \ left(t \ right)= \ sqrt {\ left [A_c + A_cK_am \ left(t \ right)+ n_I \ left(t \ right)\ right] ^ 2 + \ left(n_Q \ left(t \ right)\ right)^ 2} $$
$$ \ Rightarrow d \ left(t \ right)\ approx A_c + A_ck_am \ left(t \ right)+ n_1 \ left(t \ right)$$
復調された信号の平均電力は
$$ P_m = \ left(\ frac {A_ck_am \ left(t \ right)} {\ sqrt {2}} \ right)^ 2 = \ frac {{A_ {c}} ^ {2} {k_ {a} } ^ {2} P} {2} $$
出力でのノイズの平均パワーは
$$ P_no = WN_0 $$
代わりに、これらの値は output SNR 式。
$$ \ left(SNR \ right)_ {O、AM} = \ frac {平均\:\:電力\:\:の\:\:復調\:\:信号} {平均\:\:電力\: \:of \:\:ノイズ\:\:at \:\:出力} $$
$$ \ Rightarrow \ left(SNR \ right)_ {O、AM} = \ frac {{A_ {c}} ^ {2} {k_ {a}} ^ {2} P} {2WN_0} $$
代用、の値 Figure of merit AM受信機式の。
$$ F = \ frac {\ left(SNR \ right)_ {O、AM}} {\ left(SNR \ right)_ {C、AM}} $$
$$ \ Rightarrow F = \ left(\ frac {{A_ {c} ^ {2}} {k_ {a} ^ {2}} P} {2WN_0} \ right)/ \ left(\ frac {{A_ { c}} ^ {2} \ left(1+ {k_ {a}} ^ {2} \ right)P} {2WN_0} \ right)$$
$$ \ Rightarrow F = \ frac {{K_ {a}} ^ {2} P} {1+ {K_ {a}} ^ {2} P} $$
したがって、AM受信機の性能指数は1未満です。
DSBSCシステムでのSNR計算
ノイズを分析するために、DSBSCシステムの次の受信機モデルを検討してください。

DSBSC変調波は
$$ s \ left(t \ right)= A_cm \ left(t \ right)\ cos \ left(2 \ pi f_ct \ right)$$
DSBSC変調波の平均パワーは
$$ P_s = \ left(\ frac {A_cm \ left(t \ right)} {\ sqrt {2}} \ right)^ 2 = \ frac {{A_ {c}} ^ {2} P} {2} $$
メッセージ帯域幅のノイズの平均パワーは
$$ P_ {nc} = WN_0 $$
代わりに、これらの値は channel SNR 式。
$$ \ left(SNR \ right)_ {C、DSBSC} = \ frac {Average \:\:Power \:\:of \:\:DSBSC \:\:modulated \:\:wave} {Average \: \:電力\:\:of \:\:ノイズ\:\:in \:\:メッセージ\:\:帯域幅} $$
$$ \ Rightarrow \ left(SNR \ right)_ {C、DSBSC} = \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$
上図に示すように、チャネル内でバンドパスノイズがDSBSC変調波と混合されていると仮定します。この組み合わせは、製品変調器への入力の1つとして適用されます。したがって、この積変調器の入力は次のようになります。
$$ v_1 \ left(t \ right)= s \ left(t \ right)+ n \ left(t \ right)$$
$$ \ Rightarrow v_1 \ left(t \ right)= A_cm \ left(t \ right)\ cos \ left(2 \ pi f_ct \ right)+ \ left [n_I \ left(t \ right)\ cos \ left( 2 \ pi f_ct \ right)-n_Q \ left(t \ right)\ sin \ left(2 \ pi f_ct \ right)\ right] $$
$$ \ Rightarrow v_1 \ left(t \ right)= \ left [A_cm \ left(t \ right)+ n_I \ left(t \ right)\ right] \ cos \ left(2 \ pi f_ct \ right)-n_Q \ left(t \ right)\ sin \ left(2 \ pi f_ct \ right)$$
局部発振器は、キャリア信号$ c \ left(t \ right)= \ cos \ left(2 \ pi f_ct \ right)$を生成します。この信号は、製品変調器への別の入力として適用されます。したがって、積変調器は、$ v_1 \ left(t \ right)$と$ c \ left(t \ right)$の積である出力を生成します。
$$ v_2 \ left(t \ right)= v_1 \ left(t \ right)c \ left(t \ right)$$
上記の式の$ v_1 \ left(t \ right)$と$ c \ left(t \ right)$の値を代入します。
$$ \ Rightarrow v_2 \ left(t \ right)= \ left(\ left [A_cm \ left(t \ right)+ n_I \ left(t \ right)\ right] \ cos \ left(2 \ pi f_ct \ right )-n_Q \ left(t \ right)\ sin \ left(2 \ pi f_ct \ right)\ right)\ cos \ left(2 \ pi f_ct \ right)$$
$$ \ Rightarrow v_2 \ left(t \ right)= \ left [A_c m \ left(t \ right)+ n_I \ left(t \ right)\ right] \ cos ^ 2 \ left(2 \ pi f_ct \ right )-n_Q \ left(t \ right)\ sin \ left(2 \ pi f_ct \ right)\ cos \ left(2 \ pi f_ct \ right)$$
$$ \ Rightarrow v_2 \ left(t \ right)= \ left [A_c m \ left(t \ right)+ n_I \ left(t \ right)\ right] \ left(\ frac {1+ \ cos \ left( 4 \ pi f_ct \ right)} {2} \ right)-n_Q \ left(t \ right)\ frac {\ sin \ left(4 \ pi f_ct \ right)} {2} $$
上記の信号をローパスフィルターへの入力として適用すると、ローパスフィルターの出力は次のようになります。
$$ d \ left(t \ right)= \ frac {\ left [A_c m \ left(t \ right)+ n_I \ left(t \ right)\ right]} {2} $$
復調された信号の平均電力は
$$ P_m = \ left(\ frac {A_cm \ left(t \ right)} {2 \ sqrt {2}} \ right)^ 2 = \ frac {{A_ {c}} ^ {2} P} {8 } $$
出力でのノイズの平均パワーは
$$ P_ {no} = \ frac {WN_0} {4} $$
代わりに、これらの値は output SNR 式。
$$ \ left(SNR \ right)_ {O、DSBSC} = \ frac {平均\:\:電力\:\:の\:\:復調\:\:信号} {平均\:\:電力\: \:of \:\:ノイズ\:\:at \:\:出力} $$
$$ \ Rightarrow \ left(SNR \ right)_ {O、DSBSC} = \ left(\ frac {{A_ {c}} ^ {2} P} {8} \ right)/ \ left(\ frac {WN_0 } {4} \ right)= \ frac {{A_ {c}} ^ {2} P} {2WN_0} $$
代用、の値 Figure of merit DSBSC受信機式の。
$$ F = \ frac {\ left(SNR \ right)_ {O、DSBSC}} {\ left(SNR \ right)_ {C、DSBSC}} $$
$$ \ Rightarrow F = \ left(\ frac {{A_ {c}} ^ {2} P} {2WN_0} \ right)/ \ left(\ frac {{A_ {c}} ^ {2} P} { 2WN_0} \ right)$$
$$ \ Rightarrow F = 1 $$
したがって、DSBSC受信機の性能指数は1です。
SSBSCシステムでのSNR計算
ノイズを分析するために、SSBSCシステムの次の受信機モデルを検討してください。
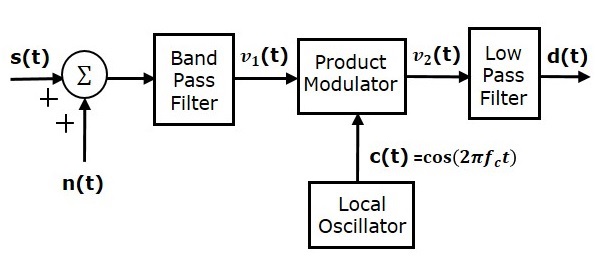
側波帯が低いSSBSC変調波は
$$ s \ left(t \ right)= \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left(f_c-f_m \ right)t \ right] $$
SSBSC変調波の平均パワーは
$$ P_s = \ left(\ frac {A_mA_c} {2 \ sqrt {2}} \ right)^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8} $$
メッセージ帯域幅のノイズの平均パワーは
$$ P_ {nc} = WN_0 $$
代わりに、これらの値は channel SNR 式。
$$ \ left(SNR \ right)_ {C、SSBSC} = \ frac {平均\:\:電力\:\:の\:\:SSBSC \:\:変調\:\:波} {平均\: \:電力\:\:の\:\:ノイズ\:\:in \:\:メッセージ\:\:帯域幅} $$
$$ \ Rightarrow \ left(SNR \ right)_ {C、SSBSC} = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$
上図に示すように、チャネル内でバンドパスノイズがSSBSC変調波と混合されていると仮定します。この組み合わせは、製品変調器への入力の1つとして適用されます。したがって、この積変調器の入力は次のようになります。
$$ v_1 \ left(t \ right)= s \ left(t \ right)+ n \ left(t \ right)$$
$$ v_1 \ left(t \ right)= \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left(f_c-f_m \ right)t \ right] + n_I \ left(t \ right)\ cos \ left(2 \ pi f_ct \ right)-n_Q \ left(t \ right)\ sin \ left(2 \ pi f_ct \ right)$$
局部発振器は、キャリア信号$ c \ left(t \ right)= \ cos \ left(2 \ pi f_ct \ right)$を生成します。この信号は、製品変調器への別の入力として適用されます。したがって、積変調器は、$ v_1 \ left(t \ right)$と$ c \ left(t \ right)$の積である出力を生成します。
$$ v_2 \ left(t \ right)= v_1 \ left(t \ right)c \ left(t \ right)$$
上記の式の$ v_1 \ left(t \ right)$と$ c \ left(t \ right)$の値を代入します。
$ \ Rightarrow v_2(t)=(\ frac {A_mA_c} {2} \ cos [2 \ pi(f_c-f_m)t] + n_I(t)\ cos(2 \ pi f_ct)-$
$ n_Q(t)\ sin(2 \ pi f_ct))\ cos(2 \ pi f_ct)$
$ \ Rightarrow v_2 \ left(t \ right)= \ frac {A_mA_c} {2} \ cos \ left [2 \ pi \ left(f_c-f_m \ right)t \ right] \ cos \ left(2 \ pi f_ct \ right)+ $
$ n_I \ left(t \ right)\ cos ^ 2 \ left(2 \ pi f_ct \ right)-n_Q \ left(t \ right)\ sin \ left(2 \ pi f_ct \ right)\ cos \ left(2 \ pi f_ct \ right)$
$ \ Rightarrow v_2 \ left(t \ right)= \ frac {A_mA_c} {4} \ left \ {\ cos \ left [2 \ pi \ left(2f_c-f_m \ right)t \ right] + \ cos \ left (2 \ pi f_mt \ right)\ right \} + $
$ n_I \ left(t \ right)\ left(\ frac {1+ \ cos \ left(4 \ pi f_ct \ right)} {2} \ right)-n_Q \ left(t \ right)\ frac {\ sin \ left(4 \ pi f_ct \ right)} {2} $
上記の信号をローパスフィルターへの入力として適用すると、ローパスフィルターの出力は次のようになります。
$$ d \ left(t \ right)= \ frac {A_mA_c} {2} \ cos \ left(2 \ pi f_mt \ right)+ \ frac {n_I \ left(t \ right)} {2} $$
復調された信号の平均電力は
$$ P_m = \ left(\ frac {A_mA_c} {4 \ sqrt {2}} \ right)^ 2 = \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} $$
出力でのノイズの平均パワーは
$$ P_ {no} = \ frac {WN_0} {4} $$
代わりに、これらの値は output SNR 式
$$ \ left(SNR \ right)_ {O、SSBSC} = \ frac {平均\:\:電力\:\:の\:\:復調\:\:信号} {平均\:\:電力\: \:of \:\:ノイズ\:\:at \:\:output} $$
$$ \ Rightarrow \ left(SNR \ right)_ {O、SSBSC} = \ left(\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {32} \ right )/ \ left(\ frac {WN_0} {4} \ right)= \ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} $$
代用、の値 Figure of merit SSBSC受信機式の
$$ F = \ frac {\ left(SNR \ right)_ {O、SSBSC}} {\ left(SNR \ right)_ {C、SSBSC}} $$
$$ F = \ left(\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ right)/ \ left(\ frac {{A_ {m}} ^ {2} {A_ {c}} ^ {2}} {8WN_0} \ right)$$
$$ F = 1 $$
したがって、SSBSC受信機の性能指数は1です。