アナログ通信-VSBSC変調
前の章では、SSBSCの変調と復調について説明しました。SSBSC変調信号には、1つの側波帯周波数しかありません。理論的には、理想的なバンドパスフィルターを使用することで、1つの側波帯周波数成分を完全に取得できます。ただし、実際には、側波帯周波数成分全体を取得できない場合があります。このため、一部の情報が失われます。
この損失を回避するために、DSBSCとSSBSCの間の妥協点である手法が選択されます。この手法は、Vestigial Side Band Suppressed Carrier (VSBSC)技術。「痕跡」という言葉は、その名前の由来となった「一部」を意味します。
VSBSC Modulationは、痕跡と呼ばれる信号の一部が1つの側波帯とともに変調されるプロセスです。VSBSC波の周波数スペクトルを次の図に示します。

この手法では、上側波帯とともに下側波帯の一部も送信されます。同様に、上側波帯の一部とともに下側波帯を送信することもできます。干渉を避けるために、VSBの両側に非常に狭い幅のガードバンドが配置されています。VSB変調は、主にテレビ送信で使用されます。
VSBSC変調の帯域幅
SSBSC変調波の帯域幅は$ f_m $であることがわかっています。VSBSC変調波には、一方の側波帯の周波数成分ともう一方の側波帯の痕跡が含まれているため、その帯域幅は、SSBSC変調波の帯域幅と痕跡周波数$ f_v $の合計になります。
i.e., Bandwidth of VSBSC Modulated Wave = $f_m + f_v$
利点
VSBSC変調の利点は次のとおりです。
非常に効率的です。
AMおよびDSBSC波と比較した場合の帯域幅の減少。
高精度を必要としないため、フィルターの設計が容易です。
低周波成分の送信は問題なく可能です。
良好な位相特性を備えています。
短所
VSBSC変調の欠点は次のとおりです。
SSBSC波と比較すると、帯域幅は広くなります。
復調は複雑です。
アプリケーション
VSBSCの最も著名で標準的なアプリケーションは、テレビ信号の送信です。また、これは、帯域幅の使用を考慮する場合に最も便利で効率的な手法です。
ここで、VSBSC波を生成する変調器とVSBSC波を1つずつ復調する復調器について説明します。
VSBSCの生成
VSBSC波の生成は、SSBSC波の生成と同様です。VSBSC変調器を次の図に示します。
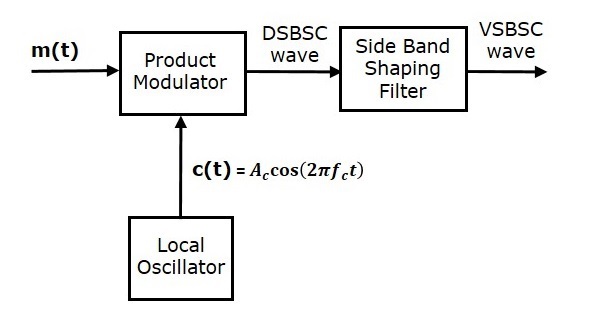
この方法では、最初に製品変調器を使用してDSBSC波を生成します。次に、このDSBSC波を側波帯整形フィルターの入力として適用します。このフィルターは、VSBSC波である出力を生成します。
変調信号$ m \ left(t \ right)$とキャリア信号$ A_c \ cos \ left(2 \ pi f_ct \ right)$は、積変調器への入力として適用されます。したがって、積変調器は、これら2つの入力の積である出力を生成します。
したがって、積変調器の出力は次のようになります。
$$ p \ left(t \ right)= A_c \ cos \ left(2 \ pi f_ct \ right)m \ left(t \ right)$$
両側にフーリエ変換を適用する
$$ P \ left(f \ right)= \ frac {A_c} {2} \ left [M \ left(f-f_c \ right)+ M \ left(f + f_c \ right)\ right] $$
上記の式は、DSBSC周波数スペクトルの式を表しています。
側波帯整形フィルターの伝達関数を$ H \ left(f \ right)$とします。このフィルターには入力$ p \ left(t \ right)$があり、出力はVSBSC変調波$ s \ left(t \ right)$です。$ p \ left(t \ right)$と$ s \ left(t \ right)$のフーリエ変換は、それぞれ$ P \ left(t \ right)$と$ S \ left(t \ right)$です。
数学的には、$ S \ left(f \ right)$を次のように書くことができます。
$$ S \ left(t \ right)= P \ left(f \ right)H \ left(f \ right)$$
上記の式に$ P \ left(f \ right)$の値を代入します。
$$ S \ left(f \ right)= \ frac {A_c} {2} \ left [M \ left(f-f_c \ right)+ M \ left(f + f_c \ right)\ right] H \ left( f \ right)$$
上記の式は、VSBSC周波数スペクトルの式を表しています。
VSBSCの復調
VSBSC波の復調は、SSBSC波の復調に似ています。ここでは、同じ搬送波信号(VSBSC波の生成に使用される)を使用してメッセージ信号を検出します。したがって、この検出プロセスは次のように呼ばれます。coherent または synchronous detection。VSBSC復調器を次の図に示します。

このプロセスでは、メッセージ信号は、VSBSC変調で使用されるキャリアの同じ周波数と位相を持つキャリアを乗算することによってVSBSC波から抽出できます。結果の信号は、ローパスフィルターを通過します。このフィルターの出力は、目的のメッセージ信号です。
VSBSC波を$ s \ left(t \ right)$とし、搬送波信号を$ A_c \ cos \ left(2 \ pi f_ct \ right)$とします。
この図から、積変調器の出力を次のように書くことができます。
$$ v \ left(t \ right)= A_c \ cos \ left(2 \ pi f_ct \ right)s \ left(t \ right)$$
両側にフーリエ変換を適用する
$$ V \ left(f \ right)= \ frac {A_c} {2} \ left [S \ left(f-f_c \ right)+ S \ left(f + f_c \ right)\ right] $$
我々は知っているH [M \(右\ F-F_C)を左+ M \は(F + F_C \右)\右から左]を\左= \ FRAC {A_C} {2}(\右F)$ S \左\左(f \ right)$
上記の式から、$ S \ left(f-f_c \ right)$と$ S \ left(f + f_c \ right)$を見つけましょう。
$$ S \ left(f-f_c \ right)= \ frac {A_c} {2} \ left [M \ left(f-f_c-f_c \ right)+ M \ left(f-f_c + f_c \ right)\右] H \ left(f-f_c \ right)$$
$ \ Rightarrow S \ left(f-f_c \ right)= \ frac {A_c} {2} \ left [M \ left(f-2f_c \ right)+ M \ left(f \ right)\ right] H \ left (f-f_c \ right)$
$$ S \ left(f + f_c \ right)= \ frac {A_c} {2} \ left [M \ left(f + f_c-f_c \ right)+ M \ left(f + f_c + f_c \ right)\右] H \ left(f + f_c \ right)$$
$ \ Rightarrow S \ left(f + f_c \ right)= \ frac {A_c} {2} \ left [M \ left(f \ right)+ M \ left(f + 2f_c \ right)\ right] H \ left (f + f_c \ right)$
$ V \ left(f \ right)$の$ S \ left(f-f_c \ right)$と$ S \ left(f + f_c \ right)$の値を代入します。
$ V(f)= \ frac {A_c} {2} [\ frac {A_c} {2} [M(f-2f_c)+ M(f)] H(f-f_c)+ $
$ \ frac {A_c} {2} [M(f)+ M(f + 2f_c)] H(f + f_c)] $
$ \ Rightarrow V \ left(f \ right)= \ frac {{A_ {c}} ^ {2}} {4} M \ left(f \ right)\ left [H \ left(f-f_c \ right) + H \ left(f + f_c \ right)\ right] $
$ + \ frac {{A_ {c}} ^ {2}} {4} \ left [M \ left(f-2f_c \ right)H \ left(f-f_c \ right)+ M \ left(f + 2f_c \ right)H \ left(f + f_c \ right)\ right] $
上記の式で、最初の項は、目的のメッセージ信号周波数スペクトルのスケーリングされたバージョンを表します。上記の信号をローパスフィルターに通すことで抽出できます。
$$ V_0 \ left(f \ right)= \ frac {{A_ {c}} ^ {2}} {4} M \ left(f \ right)\ left [H \ left(f-f_c \ right)+ H \ left(f + f_c \ right)\ right] $$