グラフ理論-カラーリング

グラフ彩色は、いくつかの制約の下で頂点、エッジ、領域などのグラフコンポーネントにラベルを付ける簡単な方法に他なりません。グラフでは、2つの隣接する頂点、隣接するエッジ、または隣接する領域が最小数の色で色付けされていません。この番号は、chromatic number グラフは properly colored graph。

グラフの彩色では、グラフに設定される制約は、色、彩色の順序、色の割り当て方法などです。彩色は、頂点または特定の領域に与えられます。したがって、同じ色を持つ頂点または領域は、独立したセットを形成します。

頂点彩色

頂点彩色は、グラフ「G」の頂点に色を割り当てて、2つの隣接する頂点が同じ色にならないようにすることです。簡単に言えば、エッジの2つの頂点が同じ色であってはなりません。

彩色数

グラフ 'G'の頂点彩色に必要な最小色数はGの彩色数と呼ばれ、X（G）で表されます。

'G'が空グラフである場合に限り、χ（G）= 1。'G'が空グラフでない場合、χ（G）≥2。

Example

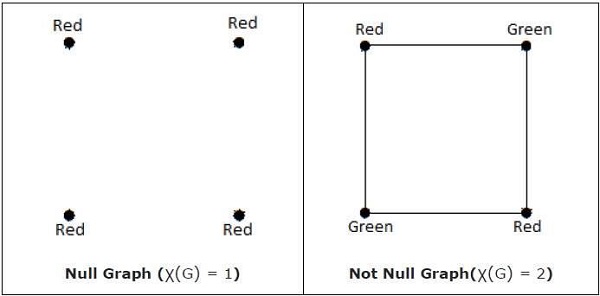
Note −グラフ 'G'は、最大n色を使用する頂点彩色がある場合、つまりX（G）≤nである場合、nでカバー可能であると言われます。

地域のカラーリング

領域の色付けは、2つの隣接する領域が同じ色にならないように、平面グラフの領域に色を割り当てることです。2つの領域が共通のエッジを持っている場合、それらは隣接していると言われます。

Example

次のグラフを見てください。領域「aeb」と「befc」は隣接しています。これは、これら2つの領域の間に共通のエッジ「be」があるためです。

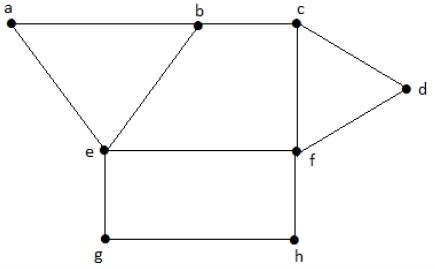
同様に、他の領域も隣接に基づいて色付けされます。このグラフは次のように色分けされています-

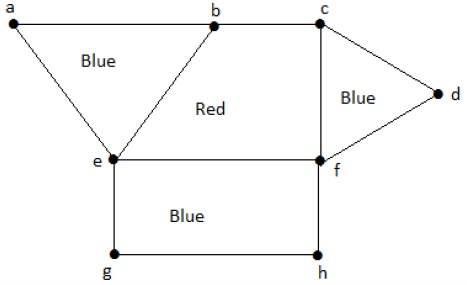
Example

Knの彩色数は

• n
• n–1
• [n/2]
• [n/2]

Kと、この例を考える₄。

完全グラフでは、各頂点は残りの（n – 1）頂点に隣接しています。したがって、各頂点には新しい色が必要です。したがって、K _n = nの彩色数。

グラフ彩色の応用

グラフ彩色は、グラフ理論の最も重要な概念の1つです。これは、次のようなコンピュータサイエンスの多くのリアルタイムアプリケーションで使用されます。

• Clustering
• データマイニング
• 画像キャプチャ
• 画像セグメンテーション
• Networking
• 資源配分
• プロセスのスケジューリング