グラフ理論-グラフの種類
頂点の数、エッジの数、相互接続性、およびそれらの全体的な構造に応じて、さまざまなタイプのグラフがあります。この章では、特定のいくつかの重要なタイプのグラフについてのみ説明します。
空グラフ
A graph having no edges ヌルグラフと呼ばれます。
例

上のグラフでは、「a」、「b」、「c」という名前の3つの頂点がありますが、それらの間にエッジはありません。したがって、それは空グラフです。
トリビアルグラフ
A graph with only one vertex トリビアルグラフと呼ばれます。
例

上に示したグラフでは、頂点 'a'は1つだけで、他のエッジはありません。したがって、それは自明なグラフです。
無向グラフ
無向グラフにはエッジが含まれていますが、エッジは有向グラフではありません。
例
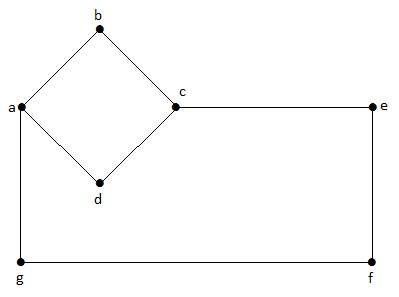
このグラフでは、「a」、「b」、「c」、「d」、「e」、「f」、「g」が頂点であり、「ab」、「bc」、「cd」、「da」です。 '、' ag '、' gf '、' ef 'はグラフの端です。これは無向グラフであるため、エッジ「ab」と「ba」は同じです。同様に、他のエッジも同じように考慮されます。
有向グラフ
有向グラフでは、各エッジに方向があります。
例

上のグラフでは、7つの頂点 'a'、 'b'、 'c'、 'd'、 'e'、 'f'、および 'g'と、8つのエッジ 'ab'、 'cb'、 ' dc '、' ad '、' ec '、' fe '、' gf '、および' ga '。有向グラフであるため、各エッジには方向を示す矢印マークが付いています。有向グラフでは、「ab」は「ba」とは異なることに注意してください。
シンプルなグラフ
グラフ with no loops といいえ parallel edges 単純グラフと呼ばれます。
'N'の頂点を持つ単一のグラフで可能なエッジの最大数はN C 2ここで、N C 2 = N(N - 1)/ 2。
'n'頂点= 2 n c 2 = 2 n(n-1)/ 2で可能な単純なグラフの数。
例
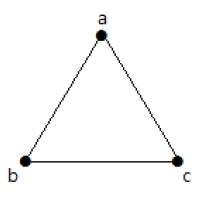
次のグラフには、平行なエッジとループを除いて最大である3つのエッジを持つ3つの頂点があります。これは、上記の式を使用して証明できます。
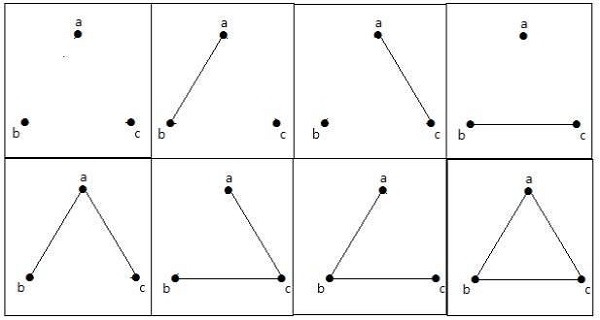
n = 3の頂点を持つエッジの最大数-
n = 3の頂点を持つ単純なグラフの最大数-
これらの8つのグラフは次のとおりです-
コネクテッドグラフ
グラフGは接続されていると言われています if there exists a path between every pair of vertices。グラフのすべての頂点に少なくとも1つのエッジが必要です。つまり、エッジの反対側にある他の頂点に接続されていると言えます。
例
次のグラフでは、各頂点に他のエッジに接続された独自のエッジがあります。したがって、それは接続されたグラフです。

切断されたグラフ
グラフGには、接続された頂点が2つ以上含まれていない場合、切断されます。
例1
次のグラフは、切断されたグラフの例です。1つは「a」、「b」、「c」、「d」の頂点を持ち、もう1つは「e」、「f」、「g」、 'h'頂点。
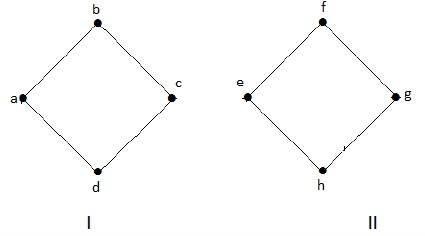
2つのコンポーネントは独立しており、相互に接続されていません。したがって、それは切断されたグラフと呼ばれます。
例2

この例では、abfeとcdの2つの独立したコンポーネントがあり、これらは互いに接続されていません。したがって、これは切り離されたグラフです。
正則グラフ
グラフGは規則的であると言われていますが、 if all its vertices have the same degree。グラフでは、各頂点の次数が「k」の場合、そのグラフは「k-正則グラフ」と呼ばれます。
例
次のグラフでは、すべての頂点の次数が同じです。したがって、これらのグラフは正則グラフと呼ばれます。
両方のグラフで、すべての頂点の次数は2です。これらは2-正則グラフと呼ばれます。
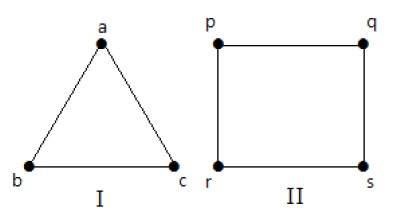
完全グラフ
'n'の相互頂点を持つ単純なグラフは完全グラフと呼ばれ、 denoted by ‘Kn’。グラフでは、a vertex should have edges with all other vertices、それからそれは完全グラフと呼ばれました。
言い換えると、頂点がグラフ内の他のすべての頂点に接続されている場合、それは完全グラフと呼ばれます。
例
次のグラフでは、グラフ内の各頂点は、それ自体を除いて、グラフ内の残りのすべての頂点に接続されています。
グラフIでは、
| A | b | c | |
|---|---|---|---|
| A | 接続されていません | 接続済み | 接続済み |
| b | 接続済み | 接続されていません | 接続済み |
| c | 接続済み | 接続済み | 接続されていません |
グラフIIでは、
| p | q | r | s | |
|---|---|---|---|---|
| p | 接続されていません | 接続済み | 接続済み | 接続済み |
| q | 接続済み | 接続されていません | 接続済み | 接続済み |
| r | 接続済み | 接続済み | 接続されていません | 接続済み |
| s | 接続済み | 接続済み | 接続済み | 接続されていません |
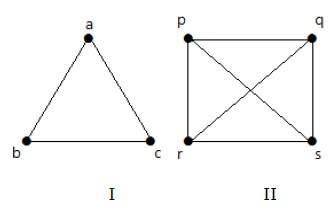
サイクルグラフ
'n'頂点(n> = 3)と 'n'エッジを持つ単純なグラフは、そのすべてのエッジが長さ 'n'のサイクルを形成する場合にサイクルグラフと呼ばれます。
グラフの各頂点の次数が2の場合、それは閉路グラフと呼ばれます。
Notation− cn
例
次のグラフを見てください-
グラフIには、サイクル「ab-bc-ca」を形成している3つのエッジを持つ3つの頂点があります。
グラフIIには、サイクル「pq-qs-sr-rp」を形成している4つのエッジを持つ4つの頂点があります。
グラフIIIには、サイクル「ik-km-ml-lj-ji」を形成している5つのエッジを持つ5つの頂点があります。

したがって、与えられたすべてのグラフは閉路グラフです。
ホイールグラフ
ホイールグラフは、新しい頂点を追加することにより、サイクルグラフCn-1から取得されます。その新しい頂点は、Hubこれは、Cの頂点全てに接続されているN。
表記法- W N
Wのエッジの数n =ハブから他のすべての頂点までのエッジの数+
ハブのない閉路グラフの他のすべてのノードからのエッジの数。
=(n–1)+(n–1)
= 2(n–1)
例
次のグラフを見てください。それらはすべてホイールグラフです。
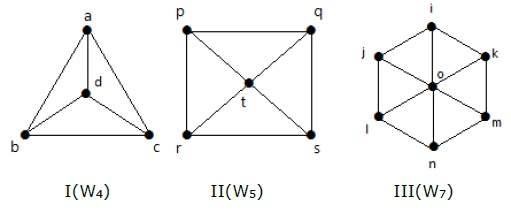
グラフIにおいて、Cから得られる3「D」と命名中央に頂点を追加することによって。これは、Wと表記される4。
W4のエッジの数= 2(n-1)= 2(3)= 6
グラフIIでは、C4から「t」という名前の頂点を中央に追加することで取得されます。これは、Wと表記される5。
W5のエッジの数= 2(n-1)= 2(4)= 8
グラフIIIには、Cから得られる6「O」と命名中央に頂点を追加することによって。これは、Wと表記される7。
W4のエッジの数= 2(n-1)= 2(6)= 12
閉路グラフ
グラフ with at least one サイクルは循環グラフと呼ばれます。
例
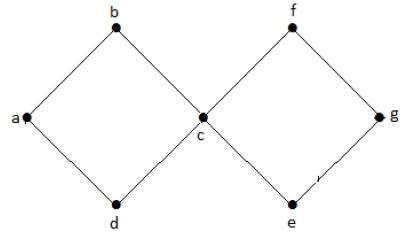
上記のグラフの例では、abcdaとcfgecの2つのサイクルがあります。したがって、それは閉路グラフと呼ばれます。
非巡回グラフ
グラフ with no cycles 非巡回グラフと呼ばれます。
例
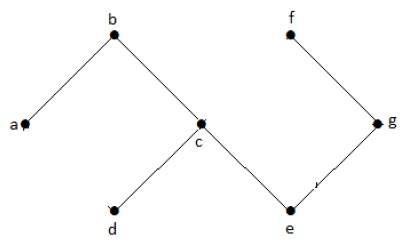
上記のグラフの例では、サイクルはありません。したがって、それは非閉路グラフです。
2部グラフ
頂点パーティションVとの単純なグラフG =(V、E)= {V 1 V、2部グラフと呼ばれています}if every edge of E joins a vertex in V1 to a vertex in V2。
一般に、Bipertiteグラフ頂点の二組を有している、私たちは、言うV1とV2、およびエッジが描かれている場合、それはセットV内の任意の頂点を接続する必要がありましょう1セットV内の任意の頂点に2。
例
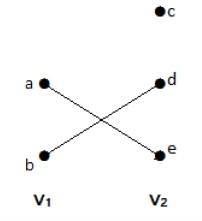
V -このグラフでは、頂点の二組を観察することができます1及びV 2を。ここで、「AE」と「BD」という名前の2つの縁部は、二組のVの頂点接続されている1及びV 2。
完全2部グラフ
パーティションVとの二部グラフ「G」、G =(V、E)= {V 1、V 2は} V内のすべての頂点の場合、完全な二部グラフであることが言われている1がVのすべての頂点に接続されている2。
一般に、完全な二部グラフは、集合Vの各頂点を接続する1セットVから各頂点に2。
例
それは集合Vの各頂点を接続するエッジ持っているので、次のグラフは、完全な二部グラフである1組のVから各頂点に2。
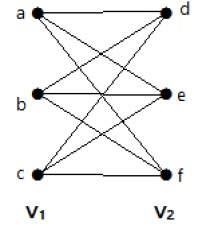
| V 1 |の場合 = mおよび| V 2 | = nの場合、完全2部グラフはK m、nで表されます。
- K m、nには、(m + n)個の頂点と(mn)個のエッジがあります。
- K m、nは、m = nの場合の正則グラフです。
一般的に、 complete bipartite graph is not a complete graph。
K m、nは、m = n = 1の場合の完全グラフです。
n個の頂点を持つ2部グラフのエッジの最大数は-です。
[N 2 /4]
もしN = 10、K5、5 = [N 2/4] = [10 2 /4] = 25。
同様に、K6、4 = 24
K7、3 = 21
K8、2 = 16
K9、1 = 9
n = 9の場合、k5、4 = [n2 / 4] = [92/4] = 20
同様に、K6、3 = 18
K7、2 = 14
K8、1 = 8
「G」に奇数の長さのサイクルがない場合、「G」は2部グラフです。2部グラフの特殊なケースはスターグラフです。
スターグラフ
K1、n-1の形式の完全2部グラフは、n個の頂点を持つスターグラフです。スターグラフは、1つの頂点が一方のセットに属し、残りのすべての頂点がもう一方のセットに属している場合、完全2部グラフです。
例
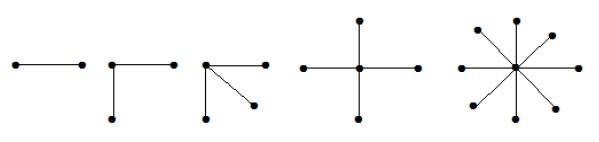
上記のグラフでは、「n」個の頂点のうち、すべての「n–1」個の頂点が単一の頂点に接続されています。したがって、スターグラフであるK 1、n-1の形式になります。
グラフの補集合
エッジがGに存在しない場合、「G-」を「G」の頂点と同じようにいくつかの頂点があり、エッジ{U、V}が「G-」に存在する単純なグラフとします。つまり、2つの頂点が隣接しています。 2つの頂点がGで隣接していない場合は、「G-」で。
グラフIに存在するエッジが別のグラフIIに存在せず、グラフIとグラフIIの両方が組み合わされて完全グラフを形成する場合、グラフIとグラフIIは互いに補数と呼ばれます。
例
次の例では、graph-Iには2つのエッジ「cd」と「bd」があります。その補グラフ-IIには4つのエッジがあります。
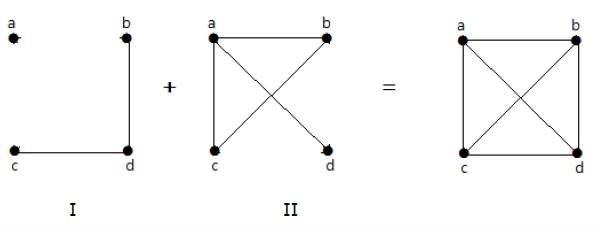
グラフIのエッジはグラフIIには存在せず、その逆も同様であることに注意してください。したがって、両方のグラフを組み合わせると、「n」個の頂点の完全グラフが得られます。
Note − 2つの補グラフを組み合わせると、完全なグラフが得られます。
'G'が単純なグラフの場合、
| E(G)| + | E( 'G-')| = | E(Kn)|、ここでn =グラフ内の頂点の数。
例
'G'を9つの頂点と12のエッジを持つ単純なグラフとし、 'G-'のエッジの数を見つけます。
あなたが持っている、| E(G)| + | E( 'G-')| = | E(Kn)|
12 + | E( 'G-')| =
9(9-1)/ 2 = 9 C 2
12 + | E( 'G-')| = 36
| E( 'G-')| = 24
「G」は40個のエッジを持つ単純なグラフであり、その補集合「G-」には38個のエッジがあります。グラフGまたは「G-」で頂点の数を見つけます。
グラフ内の頂点の数を「n」とします。
| E(G)| + | E( 'G-')| = | E(Kn)|
40 + 38 = n(n-1)/ 2
156 = n(n-1)
13(12)= n(n-1)
n = 13