グラフ理論-マッチング

マッチンググラフは、互いに隣接するエッジがないグラフのサブグラフです。単純に、2つのエッジの間に共通の頂点があってはなりません。

マッチング

'G' =（V、E）をグラフとします。サブグラフはマッチングM（G）と呼ばれ、if each vertex of G is incident with at most one edge in M、すなわち、

deg（V）≤1∀V∈G

つまり、マッチンググラフM（G）では、頂点の次数は1または0である必要があり、エッジはグラフGから入射する必要があります。

Notation − M（G）

Example

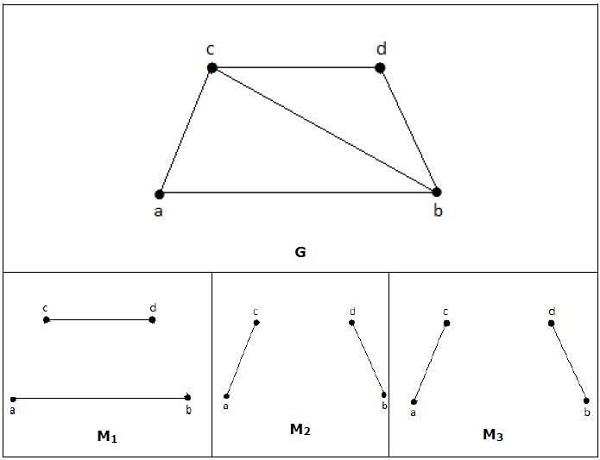
マッチングでは、

deg（V）= 1の場合、（V）は一致していると言われます

deg（V）= 0の場合、（V）は一致しません。

マッチングでは、2つのエッジが隣接していません。これは、2つのエッジが隣接している場合、それらの2つのエッジを結合している頂点の次数が2になり、マッチングルールに違反するためです。

グラフ「G」の一致するMは最大であると言われます if no other edges of ‘G’ can be added to M。

Example

上のグラフのM1、M2、M3は、Gの最大マッチングです。

これは、最大最大マッチングとも呼ばれます。最大マッチングは、エッジの最大数との最大マッチングとして定義されます。

「G」の最大マッチングにおけるエッジの数は、 matching number。

Example

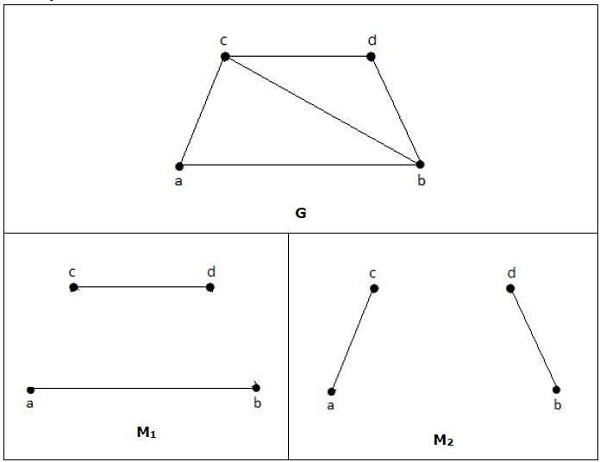
上記の例のグラフの場合、M1とM2は「G」の最大マッチングであり、そのマッチング数は2です。したがって、グラフGを使用すると、最大2つのエッジのみを持つサブグラフのみを形成できます。したがって、一致する番号は2になります。

グラフg（G）のすべての頂点が一致（M）のちょうど1つのエッジに入射する場合、グラフ（G）の一致（M）は完全一致であると言われます。

deg（V）=1∀V

サブグラフのすべての頂点の次数は1の次数である必要があります。

Example

次のグラフでは、M1とM2はGの完全一致の例です。

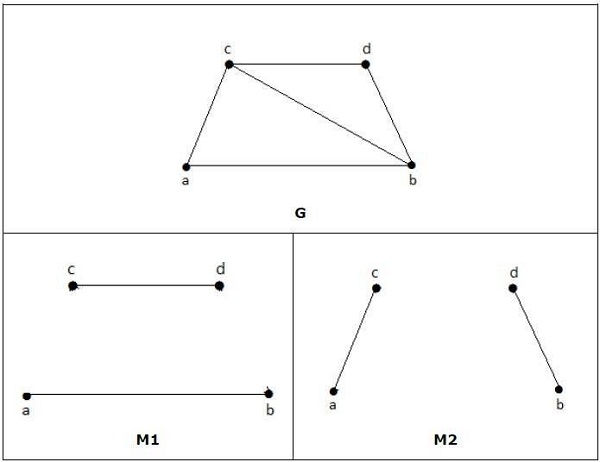
Note −完全一致グラフにエッジをもう1つ追加する可能性がないため、グラフのすべての完全一致はグラフの最大一致でもあります。

グラフの最大マッチングは完全である必要はありません。グラフ「G」が完全に一致する場合、頂点の数| V（G）| 均等です。奇数の場合、最後の頂点は他の頂点とペアになり、最後に、次数がゼロである他の頂点とペアにできない単一の頂点が残ります。それは明らかに完全一致の原則に違反しています。

Example

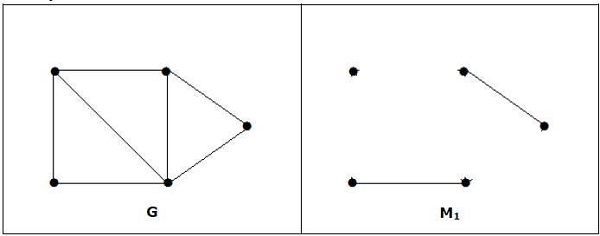
Note−上記のステートメントの逆は真である必要はありません。Gの頂点の数が偶数の場合、M1は完全である必要はありません。

Example

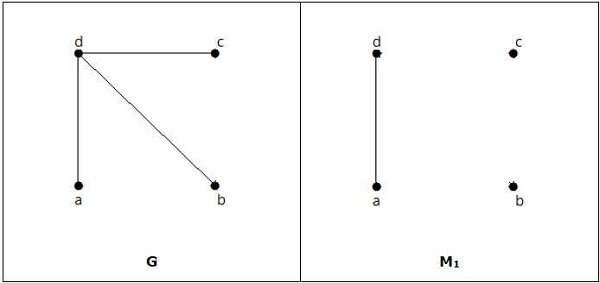
一致していますが、頂点の数が偶数であっても、完全には一致していません。