グラフ理論-独立集合

独立集合は集合で表され、

あるべきではない any edges adjacent to each other。2つのエッジの間に共通の頂点があってはなりません。
あるべきではない any vertices adjacent to each other。2つの頂点の間に共通のエッジがあってはなりません。

独立したラインセット

'G' =（V、E）をグラフとします。EのサブセットLは、Lの2つのエッジが隣接していない場合、「G」の独立したラインセットと呼ばれます。このようなセットは、独立したラインセットと呼ばれます。

Example

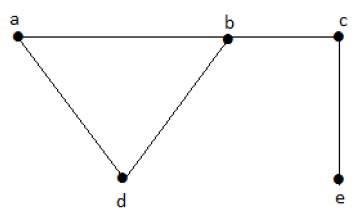
次のサブセットを考えてみましょう-

L₁ = {a,b}
L₂ = {a,b} {c,e}
L₃ = {a,d} {b,c}

この例では、サブセットL2とL3は、明らかに、指定されたグラフの隣接するエッジではありません。それらは独立したラインセットです。ただし、L1は独立したラインセットではありません。独立したラインセットを作成するには、少なくとも2つのエッジが必要です。

最大の独立したラインセット

独立線セットは、「G」の他のエッジを「L」に追加できない場合、グラフ「G」の最大の独立線セットであると言われます。

Example

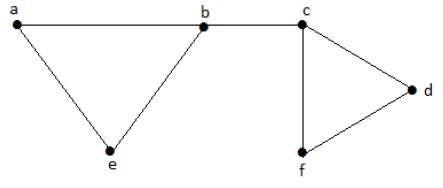
次のサブセットを考えてみましょう-

L₁ = {a, b}
L₂ = {{b, e}, {c, f}}
L₃ = {{a, e}, {b, c}, {d, f}}
L₄ = {{a, b}, {c, f}}

L ₂及びL _3は、最大の独立したラインセット/最大マッチングです。これらの2つのサブセットのみについては、隣接していない他のエッジを追加する可能性はありません。したがって、これら2つのサブセットは、最大の独立したラインセットと見なされます。

最大独立ラインセット

エッジの数が最大の「G」の最大独立線セットは、「G」の最大独立線セットと呼ばれます。

Number of edges in a maximum independent line set of G (β₁)
   = Line independent number of G
   = Matching number of G

Example

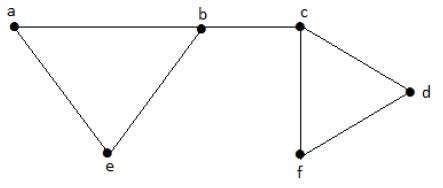
次のサブセットを考えてみましょう-

L₁ = {a, b}
L₂ = {{b, e}, {c, f}}
L₃ = {{a, e}, {b, c}, {d, f}}
L₄ = {{a, b}, {c, f}}

L ₃は、グラフ内の隣接するエッジではない最大エッジを持つGの最大独立線セットであり、β1= 3で表されます。

Note −孤立した頂点のないグラフGの場合、

α1+β1=グラフ内の頂点の数= | V |

Example

K _n / C _n / w _nの数をカバーする線、

$$ \ alpha 1 = \ lceil \ frac {n} {2} \ rceil \ begin {cases} \ frac {n} {2} \：if \：n \：is \：even \\\ frac {n + 1} {2} \：if \：n \：is \：odd \ end {cases} $$

行独立番号（マッチング数）=β ₁ = [N / 2]α ₁ +β ₁ = N。

独立した頂点セット

'G' =（V、E）をグラフとします。「S」の2つの頂点が隣接していない場合、「V」のサブセットは「G」の独立集合と呼ばれます。

Example

上記のグラフから次のサブセットを検討してください-

S₁ = {e}

S₂ = {e, f}
S₃ = {a, g, c}
S₄ = {e, d}

明らかに、S ₁は独立した頂点セットではありません。独立した頂点セットを取得するには、グラフから少なくとも2つの頂点が必要だからです。しかし、ここではそうではありません。サブセットS ₂、S ₃、及びS _4はサブセットからいずれかの頂点に隣接しない頂点が存在しないので、独立した頂点のセットです。

最大の独立した頂点セット

「G」をグラフとすると、「G」の他の頂点を「S」に追加できない場合、「G」の独立した頂点セットが最大であると言われます。

Example

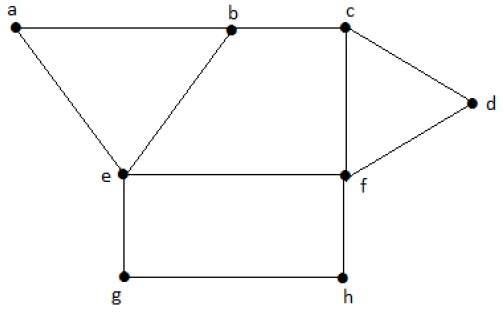
上記のグラフから次のサブセットを検討してください。

S₁ = {e}
S₂ = {e, f}
S₃ = {a, g, c}
S₄ = {e, d}

S ₂とS _3が「G」の最大独立頂点集合です。Sでは₁及びS ₄、我々は他の頂点を追加することができます。しかしSで₂及びS ₃、我々は他の頂点を追加することはできません。

最大独立頂点セット

最大数の頂点を持つ「G」の最大独立頂点セットは、最大独立頂点セットと呼ばれます。

Example

上記のグラフから次のサブセットを検討してください-

S₁ = {e}
S₂ = {e, f}
S₃ = {a, g, c}
S₄ = {e, d}

S ₃のみが、最大数の頂点をカバーするため、最大の独立した頂点セットです。「G」の最大独立頂点集合の頂点の数はGの独立した頂点数（βと呼ばれる₂）。

Example

完全グラフKnの_場合、

頂点被覆番号=α ₂ = n-1の

頂点独立番号=β ₂ = 1

あなたはα持っている₂ +β ₂ = Nを

完全グラフでは、各頂点は残りの（n − 1）頂点に隣接しています。したがって、K _nの最大独立集合には、頂点が1つだけ含まれます。

したがって、β ₂ = 1

及びα ₂ = | V | - β ₂ = n-1の

Note −任意のグラフの場合 'G' =（V、E）

α ₂ +β ₂ = | V |
「S」が「G」の独立した頂点セットである場合、（V – S）はGの頂点被覆です。