グラフ理論-基礎
グラフは、ポイントとポイントに接続された線の図です。2つの頂点のセットを結ぶ線が少なくとも1つあり、頂点がそれ自体を接続していません。グラフ理論におけるグラフの概念は、点、線、頂点、辺、頂点の次数、グラフの特性などのいくつかの基本的な用語に基づいています。ここでは、この章では、グラフ理論のこれらの基礎について説明します。
ポイント
A point1次元、2次元、または3次元空間の特定の位置です。理解を深めるために、ポイントはアルファベットで表すことができます。ドットで表すことができます。
例

ここで、ドットは「a」という名前の点です。
ライン
A Line2点間の接続です。実線で表すことができます。
Example

ここで、「a」と「b」がポイントです。これらの2点間のリンクは線と呼ばれます。
バーテックス
頂点は、複数の線が交わる点です。とも呼ばれますnode。ポイントと同様に、頂点もアルファベットで示されます。
Example

ここで、頂点はアルファベット「a」で名前が付けられています。
縁
エッジは、2つの頂点を結ぶ線の数学用語です。1つの頂点から多くのエッジを形成できます。頂点がないと、エッジを形成できません。エッジには開始頂点と終了頂点が必要です。
Example

ここで、「a」と「b」は2つの頂点であり、それらの間のリンクはエッジと呼ばれます。
グラフ
グラフ「G」は、G =(V、E)として定義されます。ここで、Vはすべての頂点のセットであり、Eはグラフ内のすべてのエッジのセットです。
Example 1

上記の例では、ab、ac、cd、およびbdがグラフのエッジです。同様に、a、b、c、およびdはグラフの頂点です。
Example 2
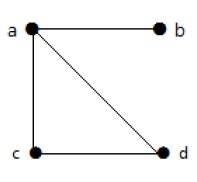
このグラフには、4つの頂点a、b、c、およびdと、4つのエッジab、ac、ad、およびcdがあります。
ループ
グラフでは、エッジが頂点からそれ自体に描画される場合、それはループと呼ばれます。
Example 1

上のグラフで、Vは、ループを形成するエッジ(V、V)を持つ頂点です。
Example 2

このグラフでは、頂点aと頂点bに形成される2つのループがあります。
頂点の次数
頂点Vに隣接する頂点の数です。
Notation − deg(V)。
n個の頂点を持つ単純なグラフでは、任意の頂点の次数は−です。
deg(v)≤n–1∀v∈G
頂点は、それ自体を除いて、他のすべての頂点とエッジを形成できます。したがって、頂点の次数は最大になりますnumber of vertices in the graph minus 1。この1は、それ自体ではループを形成できないため、自己頂点用です。いずれかの頂点にループがある場合、それは単純なグラフではありません。
頂点の次数は、グラフの2つのケースで考慮することができます-
無向グラフ
有向グラフ
無向グラフの頂点の次数
無向グラフには有向エッジがありません。次の例を検討してください。
Example 1
次のグラフを見てください-

上記の無向グラフでは、
頂点 'a'で交わる2つのエッジがあるため、deg(a)= 2です。
頂点 'b'で交わる3つのエッジがあるため、deg(b)= 3。
頂点 'c'に1つのエッジが形成されているため、deg(c)= 1
したがって、「c」は pendent vertex。
頂点 'd'で交わる2つのエッジがあるため、deg(d)= 2です。
頂点 'e'に0個のエッジが形成されているため、deg(e)= 0です。
したがって、「e」は isolated vertex。
Example 2
次のグラフを見てください-

上のグラフでは、
deg(a)= 2、deg(b)= 2、deg(c)= 2、deg(d)= 2、およびdeg(e)= 0。
頂点 'e'は孤立した頂点です。グラフにはペンダント頂点がありません。
有向グラフの頂点の次数
有向グラフでは、各頂点に indegree と outdegree。
グラフの程度
頂点Vの次数は、頂点Vに入るエッジの数です。
Notation − deg−(V)。
グラフのアウトディグリー
頂点Vのアウトディグリーは、頂点Vから出て行くエッジの数です。
Notation − deg +(V)。
次の例を検討してください。
Example 1
次の有向グラフを見てください。頂点「a」には、「ad」と「ab」の2つのエッジがあり、これらは外側に向かっています。したがって、そのアウトディグリーは2です。同様に、頂点「a」に向かってくるエッジ「ga」があります。したがって、「a」の次数は1です。

他の頂点のインディグリーとアウトディグリーを次の表に示します-
| バーテックス | インディグリー | アウトディグリー |
|---|---|---|
| A | 1 | 2 |
| b | 2 | 0 |
| c | 2 | 1 |
| d | 1 | 1 |
| e | 1 | 1 |
| f | 1 | 1 |
| g | 0 | 2 |
Example 2
次の有向グラフを見てください。頂点 'a'には、頂点 'a'から外側に向かうエッジ 'ae'があります。したがって、そのアウトディグリーは1です。同様に、グラフには頂点「a」に向かうエッジ「ba」があります。したがって、「a」の次数は1です。

他の頂点のインディグリーとアウトディグリーを次の表に示します-
| バーテックス | インディグリー | アウトディグリー |
|---|---|---|
| A | 1 | 1 |
| b | 0 | 2 |
| c | 2 | 0 |
| d | 1 | 1 |
| e | 1 | 1 |
ペンダント頂点
頂点の次数を使用することにより、2つの特別なタイプの頂点があります。次数1の頂点は、ペンダント頂点と呼ばれます。
Example

ここで、この例では、頂点「a」と頂点「b」に接続されたエッジ「ab」があります。したがって、頂点「a」に関しては、頂点「b」に向かってエッジが1つだけであり、同様に、頂点「b」に関しては、頂点「a」に向かってエッジが1つだけです。最後に、頂点 'a'と頂点 'b'の次数は、ペンダント頂点とも呼ばれます。
孤立した頂点
次数がゼロの頂点は、孤立頂点と呼ばれます。
Example

ここで、頂点 'a'と頂点 'b'は、相互に接続されておらず、他の頂点にも接続されていません。したがって、頂点「a」と「b」の両方の次数はゼロです。これらは、孤立した頂点とも呼ばれます。
隣接性
ここに隣接の規範があります-
グラフでは、2つの頂点は adjacent、2つの頂点の間にエッジがある場合。ここで、頂点の隣接性は、これら2つの頂点を接続している単一のエッジによって維持されます。
グラフでは、2つのエッジの間に共通の頂点がある場合、2つのエッジは隣接していると言われます。ここで、エッジの隣接性は、2つのエッジを接続している単一の頂点によって維持されます。
Example 1
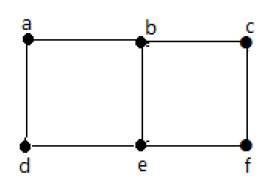
上のグラフでは-
「a」と「b」は隣接する頂点です。これらの間に共通のエッジ「ab」があるためです。
「a」と「d」は隣接する頂点です。これらの間に共通のエッジ「ad」があるためです。
ab 'と' be 'は隣接するエッジです。これは、それらの間に共通の頂点' b 'があるためです。
be 'と' de 'は隣接するエッジであり、それらの間に共通の頂点' e 'があります。
Example 2
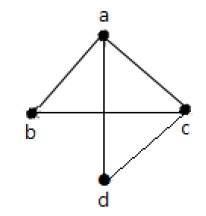
上のグラフでは-
「a」と「d」は隣接する頂点です。これらの間に共通のエッジ「ad」があるためです。
「c」と「b」は隣接する頂点です。これらの間に共通のエッジ「cb」があるためです。
「ad」と「cd」は隣接するエッジです。これらの間に共通の頂点「d」があるためです。
「ac」と「cd」は隣接するエッジです。これらの間に共通の頂点「c」があるためです。
平行辺
グラフでは、頂点のペアが複数のエッジで接続されている場合、それらのエッジは平行エッジと呼ばれます。
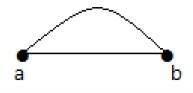
上のグラフでは、「a」と「b」は、それらの間の2つのエッジ「ab」と「ab」によって接続されている2つの頂点です。したがって、それは平行エッジと呼ばれます。
マルチグラフ
平行なエッジを持つグラフは、マルチグラフと呼ばれます。
Example 1

上のグラフには、「ab」、「ac」、「cd」、「cd」、「bd」の5つのエッジがあります。'c'と 'd'の間に2つの平行なエッジがあるため、マルチグラフになります。
Example 2
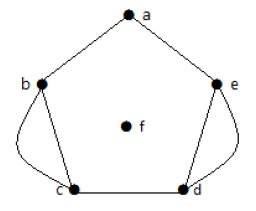
上のグラフでは、頂点「b」と「c」に2つのエッジがあります。頂点「e」と「d」にも2つのエッジがあります。したがって、それはマルチグラフです。
グラフの次数シーケンス
グラフ内のすべての頂点の次数が降順または昇順で配置されている場合、取得されたシーケンスはグラフの次数シーケンスと呼ばれます。
Example 1

| バーテックス | A | b | c | d | e |
|---|---|---|---|---|---|
| への接続 | 紀元前 | 広告 | 広告 | c、b、e | d |
| 程度 | 2 | 2 | 2 | 3 | 1 |
上のグラフでは、頂点{d、a、b、c、e}の場合、次数シーケンスは{3、2、2、2、1}です。
Example 2

| バーテックス | A | b | c | d | e | f |
|---|---|---|---|---|---|---|
| への接続 | b、e | 交流 | b、d | c、e | 広告 | - |
| 程度 | 2 | 2 | 2 | 2 | 2 | 0 |
上のグラフでは、頂点{a、b、c、d、e、f}の場合、次数シーケンスは{2、2、2、2、2、0}です。