グラフ理論-横断可能性

同じパスをたどることなく、すべての頂点間にパスを描画できる場合、グラフはトラバース可能です。このパスに基づいて、この章で説明するオイラーのパスやオイラーの回路などのいくつかのカテゴリがあります。

オイラーの道

オイラーのパスには、「G」の各エッジが1回だけ含まれ、「G」の各頂点が少なくとも1回含まれます。接続されたグラフGは、オイラーのパスが含まれている場合、トラバース可能であると言われます。

Example

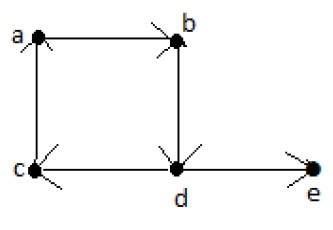
オイラーのパス= dcabde。

オイラーの回路

オイラーのパスでは、開始頂点が終了頂点と同じである場合、それはオイラー回路と呼ばれます。

Example

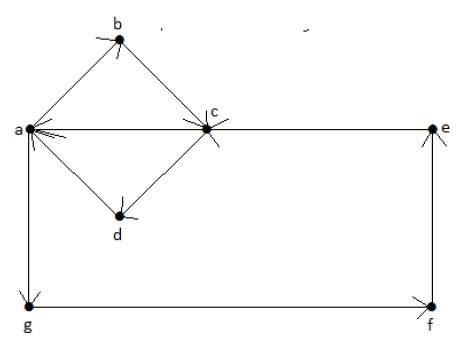
Euler’s Path = abcdagfeca。

オイラーの回路定理

連結グラフ「G」は、Gの次数が奇数の頂点の数が正確に2または0である場合にのみトラバース可能です。連結グラフGは、オイラーのパスを含むことができますが、オイラーの回路を含めることはできません。奇妙な程度。

Note −このオイラーパスは、奇数次数の頂点で始まり、奇数次数の他の頂点で終わります。

Example

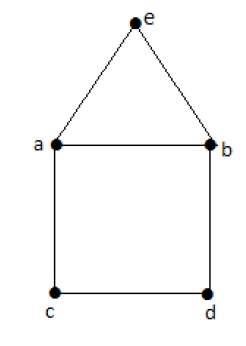
Euler’s Path− beabdcaはオイラーの回路ではありませんが、オイラーの経路です。明らかに、2つの奇数次数の頂点があります。

Note −連結グラフGで、次数が奇数の頂点の数= 0の場合、オイラーの回路が存在します。

ハミルトングラフ

連結グラフGは、Gのすべての頂点を含むサイクルが存在する場合、ハミルトングラフと呼ばれます。

すべてのサイクルは回路ですが、回路には複数のサイクルが含まれる場合があります。このようなサイクルは、Hamiltonian cycle Gの。

ハミルトンパス

接続されたグラフは、Gの各頂点が1回だけ含まれている場合、ハミルトンと呼ばれます。このようなパスは、Hamiltonian path。

Example

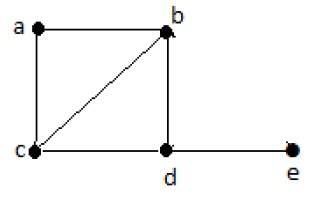
Hamiltonian Path−edbac。

Note

• オイラーの回路には、グラフの各エッジが1回だけ含まれています。

• ハミルトン閉路では、グラフの一部のエッジをスキップできます。

Example

次のグラフを見てください-

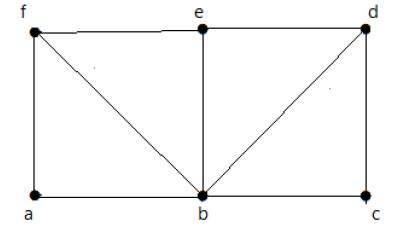
上記のグラフの場合-

• オイラーパスが存在します– false

• オイラー回路が存在する– false

• ハミルトン閉路が存在する– true

• ハミルトン経路が存在する– true

Gには、次数が奇数の4つの頂点があるため、通過できません。内部エッジをスキップすることにより、グラフはすべての頂点を通過するハミルトン閉路を持ちます。