グラフ理論-連結性

ある頂点から別の頂点にグラフをトラバースできるかどうかは、グラフがどのように接続されているかによって決まります。接続性はグラフ理論の基本的な概念です。接続性は、グラフが接続されているか切断されているかを定義します。エッジ接続と頂点接続として知られる、エッジと頂点に基づくサブトピックがあります。それらについて詳しく説明しましょう。

接続性

グラフは connected if there is a path between every pair of vertex。すべての頂点から他の頂点まで、トラバースするためのパスが必要です。これは、グラフの接続性と呼ばれます。複数の切断された頂点とエッジを持つグラフは、切断されていると言われます。

Example 1

次のグラフでは、1つの頂点から他の頂点に移動することができます。たとえば、パス「ab-e」を使用して、頂点「a」から頂点「e」にトラバースできます。

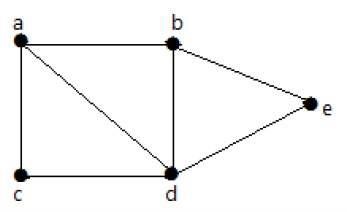
Example 2

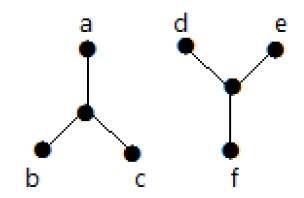
次の例では、頂点 'a'から頂点 'f'へのトラバースは、それらの間に直接または間接的にパスがないため不可能です。したがって、それは切り離されたグラフです。

切断点

'G'を連結グラフとします。頂点V∈Gは、「G-V」（「G」から「V」を削除）によってグラフが切断される場合、「G」の切断点と呼ばれます。グラフから切断点を削除すると、2つ以上のグラフに分割されます。

Note −切断点を削除すると、グラフが切断される場合があります。

接続されたグラフ「G」には、最大（n–2）個のカット頂点があります。

Example

次のグラフでは、頂点「e」と「c」がカットされた頂点です。

'e'または 'c'を削除すると、グラフは切断されたグラフになります。

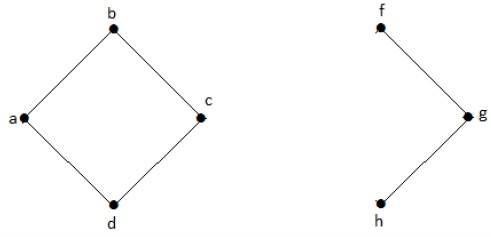
'g'がないと、頂点 'c'と頂点 'h'および他の多くの間にパスがありません。したがって、それは切断点が「e」である切断されたグラフです。同様に、「c」も上のグラフの切断点です。

カットエッジ（ブリッジ）

'G'を連結グラフとします。エッジ 'e'∈Gは、' G-e 'によってグラフが切断される場合、カットエッジと呼ばれます。

グラフのエッジを削除すると2つ以上のグラフになる場合、そのエッジはカットエッジと呼ばれます。

Example

次のグラフでは、カットエッジは[（c、e）]です。

グラフからエッジ（c、e）を削除すると、切り離されたグラフになります。

上のグラフでは、エッジ（c、e）を削除すると、グラフが2つに分割されます。これは、切断されたグラフにすぎません。したがって、エッジ（c、e）はグラフのカットエッジです。

Note −「G」を「n」個の頂点を持つ連結グラフとすると、

• エッジ 'e'がGのどのサイクルの一部でもない場合に限り、カットエッジe∈G。

• 可能なカットエッジの最大数は「n-1」です。

• 切断されたエッジの少なくとも1つの頂点が切断された頂点であるため、切断されたエッジが存在する場合は常に、切断された頂点も存在します。

• 切断点が存在する場合、切断エッジが存在する場合と存在しない場合があります。

グラフのカットセット

'G' =（V、E）を連結グラフとします。EのサブセットE 'は、GからE'のすべてのエッジを削除すると、Gが切断される場合、Gのカットセットと呼ばれます。

グラフから特定の数のエッジを削除するとグラフが切断される場合、それらの削除されたエッジはグラフのカットセットと呼ばれます。

Example

次のグラフを見てください。そのカットセットはE1 = {e1、e3、e5、e8}です。

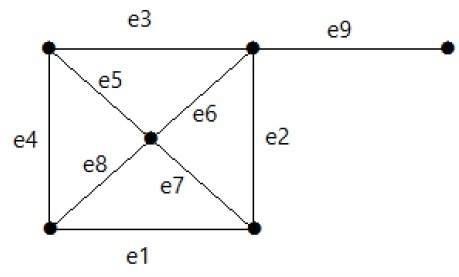
グラフからカットセットE1を削除すると、次のように表示されます。

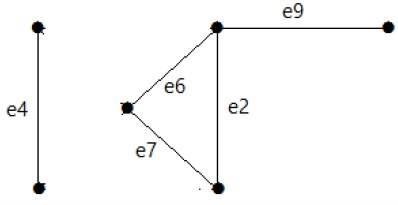
同様に、グラフを切断できる他のカットセットがあります-

• E3 = {e9} –グラフの最小カットセット。

• E4 = {e3、e4、e5}

エッジ接続

'G'を連結グラフとします。削除すると「G」が切断されるエッジの最小数は、Gのエッジ接続と呼ばれます。

Notation −λ（G）

言い換えれば、 number of edges in a smallest cut set of G Gのエッジ接続と呼ばれます。

'G'にカットエッジがある場合、λ（G）は1です（Gのエッジ接続）。

Example

次のグラフを見てください。2つの最小エッジを削除すると、接続されたグラフが切断されます。したがって、そのエッジ接続性（λ（G））は2です。

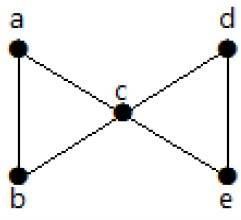
2つのエッジを削除してグラフを切断する4つの方法は次のとおりです-

頂点接続

'G'を連結グラフとします。削除によって「G」が切断されるか、「G」が簡単なグラフに縮小される頂点の最小数は、頂点接続と呼ばれます。

Notation − K（G）

Example

上のグラフでは、頂点「e」と「i」を削除すると、グラフが切断されます。

Gに切断点がある場合、K（G）= 1です。

Notation −接続されたグラフGの場合、

K（G）≤λ（G）≤δ（G）

頂点連結（K（G））、エッジ連結（λ（G））、G（δ（G））の最小度数。

Example

次のグラフのλ（G）とK（G）を計算します-

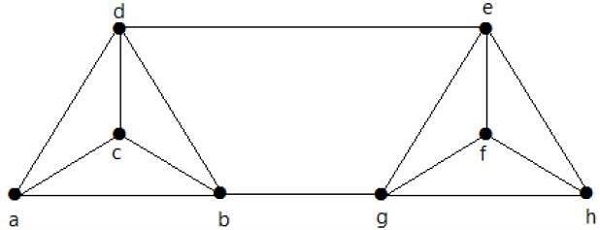
Solution

グラフから、

δ（G）= 3

K（G）≤λ（G）≤δ（G）= 3（1）

K（G）≥2（2）

エッジ{d、e}と{b、h}を削除すると、Gを切断できます。

したがって、

λ（G）= 2

2≤λ（G）≤δ（G）= 2（3）

（2）と（3）から、頂点連結K（G）= 2