グラフ理論-カバー
カバーグラフは、他のグラフに対応するすべての頂点またはすべてのエッジを含むサブグラフです。すべての頂点を含むサブグラフは、line/edge covering。すべてのエッジを含むサブグラフは、vertex covering。
ラインカバー
G =(V、E)をグラフとします。サブセットC(E)は、Gのすべての頂点がCの少なくとも1つのエッジに入射する場合、Gをカバーするラインと呼ばれます。
deg(V)≥1∀V∈G
各頂点がエッジによって別の頂点に接続されているためです。したがって、最小次数は1です。
Example
次のグラフを見てください-
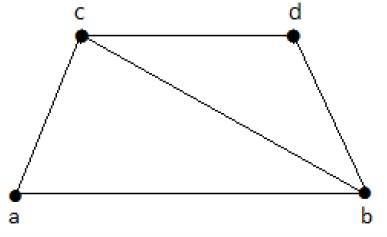
ラインカバーのあるサブグラフは次のとおりです。
C 1 = {{a、b}、{c、d}}
C 2 = {{a、d}、{b、c}}
C 3 = {{a、b}、{b、c}、{b、d}}
C 4 = {{a、b}、{b、c}、{c、d}}
'G'が孤立した頂点を持っている場合に限り、 'G'のラインカバーは存在しません。'n'頂点を持つグラフの線被覆には、少なくとも[n / 2]個のエッジがあります。
最小限のラインカバー
グラフGのCを覆う線は最小と言われます if no edge can be deleted from C。
Example
上のグラフで、線をカバーするサブグラフは次のとおりです。
C 1 = {{a、b}、{c、d}}
C 2 = {{a、d}、{b、c}}
C 3 = {{a、b}、{b、c}、{b、d}}
C 4 = {{a、b}、{b、c}、{c、d}}
ここで、C 1、C 2、C 3は最小限のラインカバーですが、C 4は{b、c}を削除できるためではありません。
最小ラインカバー
としても知られています Smallest Minimal Line Covering。エッジの数が最小の最小ラインカバーは、「G」の最小ラインカバーと呼ばれます。'G'でカバーする最小ラインのエッジの数は、line covering number(α 'G'の1)。
Example
上記の例では、C 1及びC 2は、 Gの被覆最小線であり、α 1 = 2。
すべてのラインカバーには、最小限のラインカバーが含まれています。
被覆最小線が含まれていないすべての行被覆(C 3は、任意の最小線被覆を含んでいません。
最小限のラインカバーにはサイクルが含まれていません。
「C」をカバーする線に長さ3以上のパスが含まれていない場合、「C」のすべてのコンポーネントはスターグラフであり、スターグラフからエッジを削除できないため、「C」は最小のラインカバーです。
頂点被覆
'G' =(V、E)をグラフとします。VのサブセットKは、「G」のすべてのエッジが「K」の頂点に入射するか、頂点で覆われている場合、「G」の頂点被覆と呼ばれます。
Example
次のグラフを見てください-
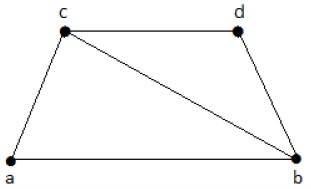
上記のグラフから導き出せるサブグラフは次のとおりです。
K 1 = {b、c}
K 2 = {a、b、c}
K 3 = {b、c、d}
K 4 = {a、d}
ここで、K 1、K 2、およびK 3には頂点被覆がありますが、K 4はエッジ{bc}を覆わないため、頂点被覆はありません。
最小限の頂点被覆
グラフ「G」の頂点「K」は、「K」から頂点を削除できない場合、最小頂点被覆であると言われます。
Example
上のグラフで、頂点被覆を持つサブグラフは次のとおりです。
K 1 = {b、c}
K 2 = {a、b、c}
K 3 = {b、c、d}
ここで、K 1及びK 2は、 Kで、一方、最小頂点被覆されている3、頂点「d」は削除することができます。
最小頂点被覆
これは、最小の最小頂点被覆としても知られています。頂点の数が最小のグラフ「G」の最小頂点被覆は、最小頂点被覆と呼ばれます。
「G」の最小頂点被覆の頂点の数は、(αGの数をカバーする頂点と呼ばれる2)。
Example
次のグラフでは、頂点被覆を持つサブグラフは次のとおりです。
K 1 = {b、c}
K 2 = {a、b、c}
K 3 = {b、c、d}

ここで、K 1は2つの頂点しかないため、Gの最小頂点被覆です。α 2 = 2。