グラフ理論-例
この章では、前の章ですでに説明した概念を示すために、いくつかの標準的な例を取り上げます。
例1
Find the number of spanning trees in the following graph.
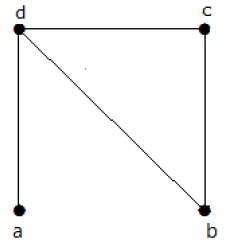
解決
上のグラフから得られた全域木の数は3本です。
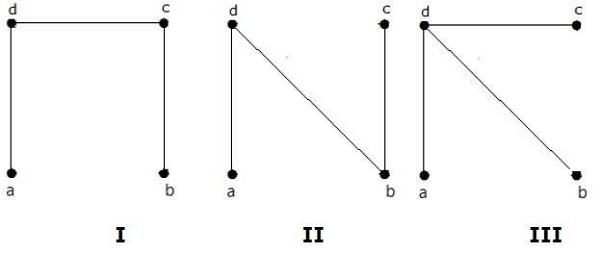
これらの3つは、特定のグラフのスパニングツリーです。ここで、グラフIとIIは互いに同型です。明らかに、非同型スパニングツリーの数は2つです。
例2
How many simple non-isomorphic graphs are possible with 3 vertices?
解決
3つの頂点で可能な4つの非同型グラフがあります。それらを以下に示します。
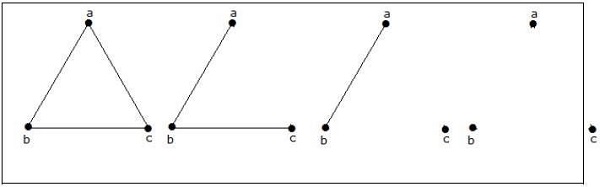
例3
Let ‘G’ be a connected planar graph with 20 vertices and the degree of each vertex is 3. Find the number of regions in the graph.
解決
度の定理の合計により、
20Σi= 1 deg(Vi)= 2 | E |
20(3)= 2 | E |
| E | = 30
オイラーの公式により、
| V | + | R | = | E | + 2
20歳以上| R | = 30 + 2
| R | = 12
したがって、リージョンの数は12です。
例4
What is the chromatic number of complete graph Kn?
解決
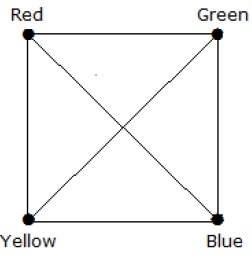
完全グラフでは、各頂点は残りの(n–1)頂点に隣接しています。したがって、各頂点には新しい色が必要です。したがって、彩色数K n = nです。
例5
What is the matching number for the following graph?
解決
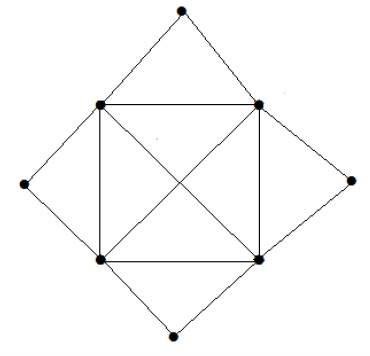
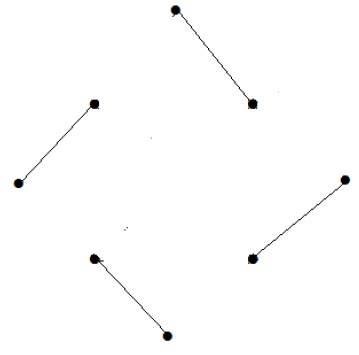
頂点の数= 9
一致できる頂点は8つだけです。
一致する番号は4です。
例6
What is the line covering number of for the following graph?
解決
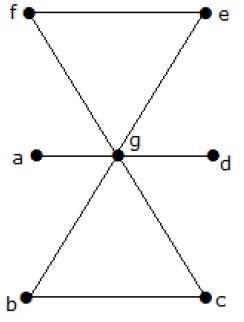
頂点の数= | V | = n = 7
行カバー数=(α 1)≥[N / 2] = 3
α 1 ≥3
3つのエッジを使用することで、すべての頂点をカバーできます。
したがって、番号をカバーする行は3です。