グラフ理論-同型
グラフは、同じ数の頂点、エッジ、および同じエッジ接続を持つさまざまな形式で存在できます。このようなグラフは同型グラフと呼ばれます。この章では、主にグラフを参照し、相互に認識することを目的として、グラフにラベルを付けていることに注意してください。
同型グラフ
二つのグラフG 1及びG 2が場合同型であると言われています-
コンポーネント(頂点とエッジ)の数は同じです。
それらのエッジ接続は保持されます。
Note−要するに、2つの同型グラフのうち、一方は他方の微調整バージョンです。ラベルのないグラフは、同型グラフと考えることもできます。
There exists a function ‘f’ from vertices of G1 to vertices of G2
[f: V(G1) ⇒ V(G2)], such that
Case (i): f is a bijection (both one-one and onto)
Case (ii): f preserves adjacency of vertices, i.e., if the edge {U, V} ∈ G1, then the
edge {f(U), f(V)} ∈ G2, then G1 ≡ G2.Note
Gもし1 ≡G 2、次いで-
| V(G 1)| = | V(G 2)|
| E(G 1)| = | E(G 2)|
Gの程度の配列1及びG 2は同一です。
頂点場合{V 1、V 2、.. Vkは} Gにおける長さKのサイクルを形成する1は、頂点{F(V 1)、F(V 2)、...、F(VKが)}サイクルを形成すべきですGの長さKの2。
グラフGのために上記のすべての条件が必要である1及びG 2は、グラフは同型であることを証明するのに十分な同形ではなくなるように。
(G 1 ≡G 2)及び場合だけ(G 1 - ≡G 2 - )ここで、G 1及びG 2は、単純なグラフです。
(G 1 ≡G 2)Gの隣接行列場合1及びG 2は同一です。
(G 1 ≡G 2)であれば、Gの対応するサブグラフ場合にのみ1とG 2(グラフGにおいて、いくつかのG1内の頂点とその画像を削除することによって得られる2)同型です。
Example
次のグラフのどれが同型ですか?
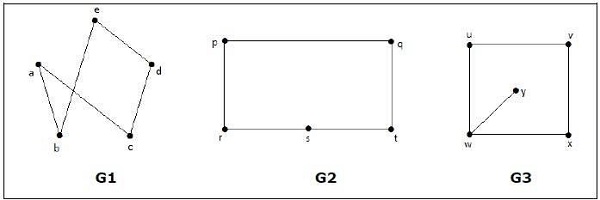
グラフGにおいて3、3のみ度を有する「W」頂点は、他のすべてのグラフの頂点に対し、したがってGと同形ではないG3度2を有する1又はG 2。
Gの補撮影1およびG 2を、あなたが持っています-
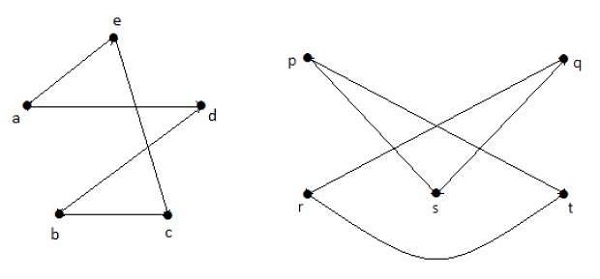
ここで、(G 1 - ≡G 2 - )、したがって(G 1 ≡G 2)。
平面グラフ
グラフ「G」は、2つのエッジが非頂点で互いに交差しないように平面または球上に描画できる場合、平面であると言われます。
Example
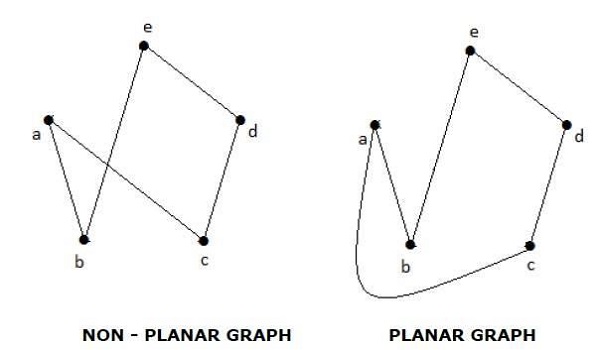
地域
すべての平面グラフは、平面を領域と呼ばれる接続された領域に分割します。
Example
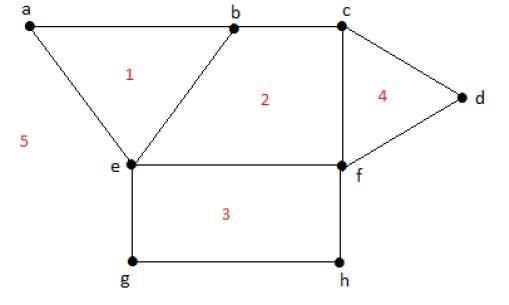
有界領域の次数 r = deg(r) =領域rを囲むエッジの数。
deg(1) = 3
deg(2) = 4
deg(3) = 4
deg(4) = 3
deg(5) = 8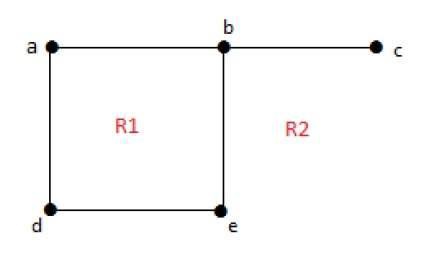
無制限の領域の程度 r = deg(r) =領域rを囲むエッジの数。
deg(R1) = 4
deg(R2) = 6平面グラフでは、次のプロパティが有効です。
'n'個の頂点を持つ平面グラフでは、すべての頂点の次数の合計は-です。
による Sum of Degrees of Regions/定理、「n」個の領域を持つ平面グラフでは、領域の次数の合計は−です。
上記の定理に基づいて、次の結論を導き出すことができます-
平面グラフでは、
各領域の次数がKの場合、領域の次数の合計は−です。
各領域の次数が少なくともK(≥K)である場合、
各領域の次数が最大でK(≤K)の場合、
Note −すべての領域の次数が同じであると想定します。
による Euler’s Formulae 平面グラフでは、
グラフ「G」が接続された平面である場合、
'K'成分を含む平面グラフの場合、
ここで、| V | は頂点の数、| E | はエッジの数であり、| R | はリージョンの数です。
エッジ頂点の不等式
'G'が、各領域の次数が少なくとも 'K'である接続された平面グラフである場合、
| E | ≤k/(k-2){| v | --2}
あなたが知っている、| V | + | R | = | E | + 2
K. | R | ≤2| E |
K(| E |-| V | + 2)≤2| E |
(K-2)| E | ≤K(| V | -2)
| E | ≤k/(k-2){| v | --2}
'G'が単純な接続平面グラフの場合、
|E| ≤ 3|V| − 6
|R| ≤ 2|V| − 4deg(V)≤5となるような頂点V•∈Gが少なくとも1つ存在します。
'G'が単純な接続平面グラフ(少なくとも2つのエッジを持つ)であり、三角形がない場合、
|E| ≤ {2|V| – 4}クラトフスキの定理
グラフ「G」は、非平面である場合に「G」はKに同相であるサブグラフている場合にのみ5またはK 3,3。
準同型
二つのグラフG 1及びG 2は、これらのグラフのそれぞれが複数の頂点とGの一部のエッジを分割して同じグラフ「G」から得ることができる場合には、準同型であると言われます。次の例を見てください-

1つの頂点を追加して、エッジ 'rs'を2つのエッジに分割します。
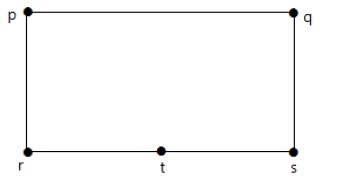
以下に示すグラフは、最初のグラフと準同型です。
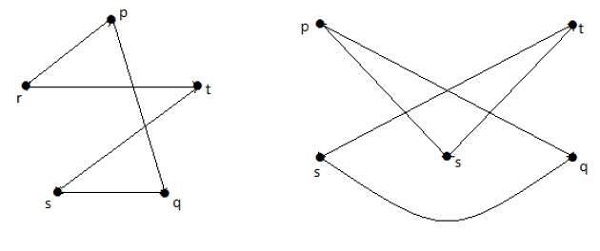
G場合1がGと同形である2は、GはG2に同相であるが、逆必要が真ではありません。
頂点が4つ以下のグラフはすべて平面です。
エッジが8以下のグラフはすべて平面です。
完全グラフK nが平面の場合に限り、N≤4です。
完全2部グラフKm 、nは、 m≤2またはn≤2の場合に限り、平面です。
頂点の最小数を有する単純な非平面グラフは、完全グラフKである5。
エッジの最小数を有する単純な非平面グラフはKである3,3。
多面体グラフ
各頂点の次数が3以上、つまりdeg(V)≥3∀V∈Gの場合、単純に接続された平面グラフは多面体グラフと呼ばれます。
3 | V | ≤2| E |
3 | R | ≤2| E |