Excel 데이터 재무 분석
Excel을 사용하여 쉽게 재무 분석을 수행 할 수 있습니다. Excel은 PMT, PV, NPV, XNPV, IRR, MIRR, XIRR 등과 같은 몇 가지 재무 기능을 제공하여 재무 분석 결과에 빠르게 도달 할 수 있도록합니다.
이 장에서는 이러한 함수를 분석에 사용할 수있는 위치와 방법에 대해 설명합니다.
연금이란 무엇입니까?
연금은 연속적인 기간에 걸쳐 이루어진 일련의 지속적인 현금 지급입니다. 예를 들어, 퇴직금, 보험료, 주택 융자, 모기지 등에 대한 저축. 연금 기능에서-
- 양수는받은 현금을 나타냅니다.
- 음수는 지불 된 현금을 나타냅니다.
일련의 향후 지불의 현재 가치
현재 가치는 일련의 향후 지불이 현재 가치가있는 총액입니다. Excel 함수를 사용하여 현재 가치를 계산할 수 있습니다-
PV− 이자율과 일련의 미래 지불 (음수 값) 및 소득 (양수 값)을 사용하여 투자의 현재 가치를 계산합니다. 현금 흐름 중 하나 이상은 양수이고 하나 이상은 음수 여야합니다.
NPV − 할인율과 일련의 정기적 인 미래 지불 (음수 값) 및 수입 (양수 값)을 사용하여 투자의 순 현재 가치를 계산합니다.
XNPV − 반드시 주기적이지 않은 현금 흐름의 순 현재 가치를 계산합니다.
Note that −
PV 현금 흐름은 일정해야하지만 NPV 현금 흐름은 가변적 일 수 있습니다.
PV 현금 흐름은 기간의 시작 또는 끝일 수 있지만 NPV 현금 흐름은 기간의 끝이어야합니다.
NPV 현금 흐름은 주기적이어야하지만 XNPV 현금 흐름은 주기적 일 필요가 없습니다.
이 섹션에서는 PV로 작업하는 방법을 이해합니다. 이후 섹션에서 NPV에 대해 배웁니다.
예
냉장고를 구입한다고 가정 해보십시오. 판매원이 냉장고 가격이 32000이라고 말하지만, 이자율이 연 13 %이고 연간 지불액이 6000 인 상태에서 8 년 내에 금액을 지불 할 수있는 옵션이 있습니다. 지불 할 수도 있습니다. 매년 초 또는 말에.
이러한 옵션 중 어떤 것이 유익한 지 알고 싶습니다.
엑셀 기능 PV를 사용할 수 있습니다-
PV (rate, nper, pmt, [fv ], [type])연말에 지불하여 현재 가치를 계산하려면 type을 생략하거나 type에 0을 지정하십시오.
매년 말에 지불하는 현재 가치를 계산하려면 유형에 1을 지정하십시오.

다음과 같은 결과를 얻을 수 있습니다.

따라서,
- 지금 지불하면 현재 가치의 32,000을 지불해야합니다.
- 연말에 지불하는 연간 지불을 선택하는 경우 현재 가치의 28,793을 지불해야합니다.
- 연말에 지불하는 연간 지불을 선택하면 현재 가치의 32,536을 지불해야합니다.
옵션 2가 당신에게 유익하다는 것을 분명히 알 수 있습니다.
EMI 란 무엇입니까?
EMI (Equated Monthly Installment)는 Investopedia에서 "매월 지정된 날짜에 차용자가 대출 기관에 지불하는 고정 지불 금액입니다. 월별 등가 할부는 매월이자와 원금을 모두 상환하는 데 사용됩니다. 지정된 기간 동안 대출금은 전액 상환됩니다. "
대출에 대한 EMI
Excel에서 PMT 기능을 사용하여 대출에 대한 EMI를 계산할 수 있습니다.
연간 이자율이 11.5 %이고 대출 기간이 25 년인 5000000의 주택 융자를 받고 싶다고 가정 해 보겠습니다. 다음과 같이 EMI를 찾을 수 있습니다.
- 월 이자율 계산 (연간 이자율 / 12)
- 월별 지불 횟수 계산 (연수 * 12)
- PMT 기능을 사용하여 EMI 계산

보시다시피
- 현재 가치 (PV)는 대출 금액입니다.
- 기간 말에 대출 금액이 0이어야하므로 미래 가치 (FV)는 0입니다.
- EMI는 매월 초에 지급되므로 유형은 1입니다.
다음과 같은 결과를 얻을 수 있습니다.

대출에 대한 원금 및이자의 월 지불
EMI에는이자 및 원금 일부 지불이 포함됩니다. 시간이 증가함에 따라 EMI의이 두 구성 요소가 달라져 균형이 떨어집니다.
얻기 위해
월별 결제의이자 부분은 Excel IPMT 기능을 사용할 수 있습니다.
월별 결제의 주요 부분은 엑셀 PPMT 기능을 사용할 수 있습니다.
예를 들어, 연간 16 %의 비율로 8 개월 동안 1,000,000의 대출을받은 경우입니다. 8 개월 동안 EMI,이자 감소, 원금 지급 증가 및 대출 잔액 감소에 대한 값을 얻을 수 있습니다. 8 개월 말에 대출 잔액은 0이됩니다.
아래의 절차를 따르십시오.
Step 1 − 다음과 같이 EMI를 계산합니다.

그 결과 Rs의 EMI가 발생합니다. 13261.59.

Step 2 − 다음으로 아래와 같이 8 개월 동안 EMI의이자와 주요 부분을 계산합니다.

다음과 같은 결과를 얻을 수 있습니다.

두 기간 사이에 지급되는이자와 원금
두 기간 사이에 지급되는이자와 원금을 계산할 수 있습니다.
이 사이에 지불 누적이자 계산 차 및 3 번째의 CUMIPMT 기능을 사용하여 개월.
2에 대한 관심 값을 합산 결과 확인 차 및 3 번째의 달을.
(2) 사이에 유료 누적 계산 주체 차 및 3 번째의 CUMPRINC 함수를 사용 개월.
2 주 값을 합산 결과 확인 차 및 3 번째의 달을.

다음과 같은 결과를 얻을 수 있습니다.

계산 결과가 확인 결과와 일치 함을 알 수 있습니다.
이자율 계산
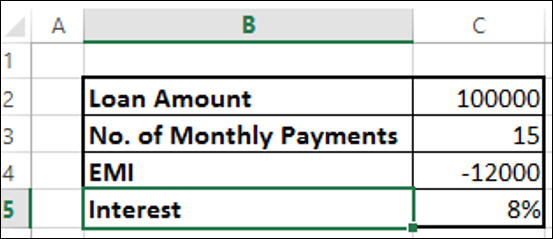
100,000의 대출을 받고 최대 월 상환액 12000으로 15 개월 내에 상환하려고한다고 가정합니다. 지불해야하는 이자율을 알고 싶을 수 있습니다.
Excel RATE 함수로 이자율을 찾으십시오-

결과는 8 %로 표시됩니다.
대출 기간 계산
10 % 이자율로 100,000의 대출을 받았다고 가정합니다. 월별 최대 지불액은 15,000입니다. 대출을 청산하는 데 걸리는 시간을 알고 싶을 수 있습니다.
Excel NPER 기능으로 결제 건수 찾기

결과는 12 개월입니다.

투자 결정
투자를 원할 때 다른 옵션을 비교하고 더 나은 수익을내는 옵션을 선택합니다. 순 현재 가치는 일정 기간 동안 현금 흐름을 비교하고 어느 것이 더 나은지 결정하는 데 유용합니다. 현금 흐름은 정기적, 주기적 간격 또는 불규칙한 간격으로 발생할 수 있습니다.
첫째, 우리는 regular, periodical cash flows.
n 년 후 (n은 분수 일 수 있음) 여러 시점에서받은 현금 흐름 시퀀스의 순 현재 가치는 다음과 같습니다. 1/(1 + r)n, 여기서 r은 연간 이자율입니다.
3 년 동안 다음 두 가지 투자를 고려하십시오.
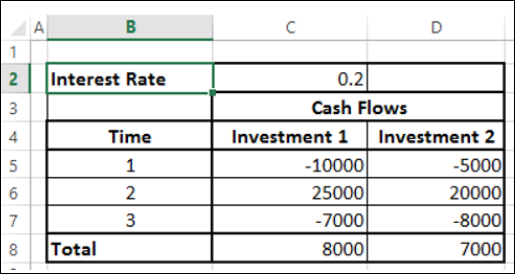
액면가로는 투자 1이 투자 2보다 낫게 보입니다. 그러나 오늘 현재 투자의 진정한 가치를 아는 경우에만 어떤 투자가 더 나은지 결정할 수 있습니다. NPV 함수를 사용하여 수익을 계산할 수 있습니다.
현금 흐름이 발생할 수 있습니다.
- 매년 말.
- 매년 초.
- 매년 중순.
NPV 함수는 현금 흐름이 연말에 있다고 가정합니다. 현금 흐름이 다른 시간에 발생하는 경우 NPV를 사용한 계산과 함께 해당 특정 요소를 고려해야합니다.
현금 흐름이 연말에 발생한다고 가정합니다. 그런 다음 NPV 기능을 바로 사용할 수 있습니다.
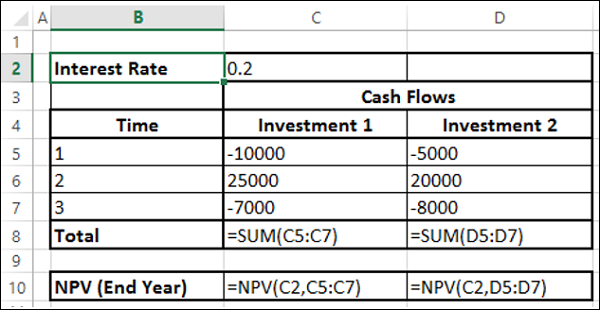
다음과 같은 결과를 얻을 수 있습니다.

투자 2의 NPV가 투자 1의 NPV보다 높다는 사실을 관찰 할 수 있으므로 투자 2가 더 나은 선택입니다. 이 결과는 투자 2의 현금 유출 흐름이 투자 1의 현금 흐름과 비교하여 나중에 있기 때문입니다.
연초 현금 흐름
매년 초에 현금 흐름이 발생한다고 가정합니다. 이 경우 이미 현재 가치를 나타내므로 NPV 계산에 첫 번째 현금 흐름을 포함해서는 안됩니다. 순 현재 가치를 얻으려면 나머지 현금 흐름에서 얻은 NPV에 첫 번째 현금 흐름을 더해야합니다.

다음과 같은 결과를 얻을 수 있습니다.

연중 현금 흐름
현금 흐름이 매년 중반에 발생한다고 가정합니다. 이 경우 현금 흐름에서 얻은 NPV에 $ \ sqrt {1 + r} $를 곱하여 순 현재 가치를 구해야합니다.

다음과 같은 결과를 얻을 수 있습니다.

불규칙한 간격의 현금 흐름
불규칙한 현금 흐름, 즉 임의의 시간에 발생하는 현금 흐름으로 순 현재 가치를 계산하려면 계산이 약간 복잡합니다.
그러나 Excel에서는 XNPV 함수를 사용하여 이러한 계산을 쉽게 수행 할 수 있습니다.
- 날짜와 현금 흐름으로 데이터를 정렬하십시오.
Note− 데이터의 첫 번째 날짜는 모든 날짜 중 가장 빠른 날짜 여야합니다. 다른 날짜는 임의의 순서로 나타날 수 있습니다.
- XNPV 함수를 사용하여 순 현재 가치를 계산합니다.
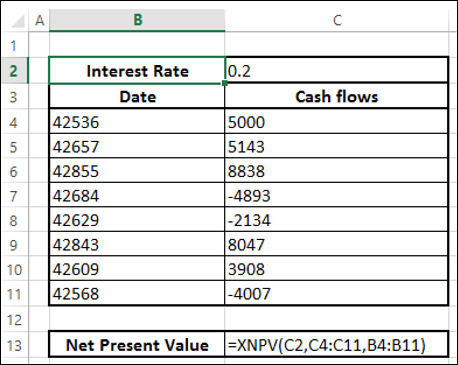
다음과 같은 결과를 얻을 수 있습니다.

가정하자 오늘 날짜가 15 일 이 관찰 월, 2015 년, 현금 흐름의 모든 날짜 이후 날짜의이다. 오늘의 순 현재 가치를 찾으려면 상단의 데이터에 포함하고 현금 흐름에 0을 지정하십시오.

다음과 같은 결과를 얻을 수 있습니다.

내부 수익률 (IRR)
투자의 내부 수익률 (IRR)은 NPV가 0 인 이자율입니다. 이는 양의 현금 흐름의 현재 가치가 음의 값을 정확히 보상하는 이율 값입니다. 할인율이 IRR이면 투자는 완전히 무관심합니다. 즉, 투자자는 돈을 벌거나 잃지 않습니다.
다음 현금 흐름, 다른 이자율 및 해당 NPV 값을 고려하십시오.

이자율 10 %와 11 % 사이에서 관찰 할 수 있듯이 NPV의 부호가 바뀝니다. 이자율을 10.53 %로 미세 조정하면 NPV는 거의 0입니다. 따라서 IRR은 10.53 %입니다.
프로젝트에 대한 현금 흐름의 IRR 결정
Excel 함수 IRR을 사용하여 현금 흐름의 IRR을 계산할 수 있습니다.

IRR은 이전 섹션에서 본 것처럼 10.53 %입니다.
주어진 현금 흐름에 대해 IRR은-
- 존재하고 독특하다
- 존재하고 여러
- 존재하지 않는다
고유 IRR
IRR이 존재하고 고유 한 경우 여러 가능성 중에서 최상의 투자를 선택하는 데 사용할 수 있습니다.
첫 번째 현금 흐름이 음수이면 투자자에게 돈이 있고 투자를 원한다는 의미입니다. 그런 다음 IRR이 높을수록 투자자가받는 이자율을 나타내므로 더 좋습니다.
첫 번째 현금 흐름이 양수이면 투자자가 돈이 필요하고 대출을 찾고 있음을 의미하며, 투자자가 지불하는 이자율을 나타내므로 IRR이 낮을수록 좋습니다.
IRR이 고유한지 여부를 찾으려면 추측 값을 변경하고 IRR을 계산하십시오. IRR이 일정하게 유지되면 고유합니다.

보시다시피 IRR은 다양한 추측 값에 대해 고유 한 값을 갖습니다.

여러 IRR
어떤 경우에는 여러 IRR이있을 수 있습니다. 다음 현금 흐름을 고려하십시오. 다른 추측 값으로 IRR을 계산합니다.

다음과 같은 결과를 얻을 수 있습니다.

-9.59 %와 216.09 %의 두 가지 IRR이 있음을 알 수 있습니다. NPV를 계산하는이 두 IRR을 확인할 수 있습니다.

-9.59 % 및 216.09 % 모두에 대해 NPV는 0입니다.
IRR 없음
어떤 경우에는 IRR이 없을 수도 있습니다. 다음 현금 흐름을 고려하십시오. 다른 추측 값으로 IRR을 계산합니다.

모든 추측 값에 대해 #NUM으로 결과를 얻습니다.

결과 #NUM은 고려 된 현금 흐름에 대한 IRR이 없음을 의미합니다.
현금 흐름 패턴 및 IRR
현금 흐름에 부호가 음수에서 양수로 또는 양수에서 음수로 한 번만 변경되는 경우 고유 한 IRR이 보장됩니다. 예를 들어, 자본 투자에서 첫 번째 현금 흐름은 음수이고 나머지 현금 흐름은 양수입니다. 이러한 경우 고유 IRR이 존재합니다.
현금 흐름에 둘 이상의 기호 변경이있는 경우 IRR이 존재하지 않을 수 있습니다. 존재하더라도 고유하지 않을 수 있습니다.
IRR에 기반한 결정
많은 분석가가 IRR을 선호하며, 백분율로 표시되는 것이 이해하기 쉽고 필요한 수익과 비교하기 쉽기 때문에 인기있는 수익성 측정입니다. 그러나 IRR로 결정을 내리는 동안 특정 문제가 있습니다. IRR로 순위를 매기고 이러한 순위에 따라 결정을 내리면 잘못된 결정을 내릴 수 있습니다.
NPV를 통해 재정적 결정을 내릴 수 있음을 이미 보셨습니다. 그러나 IRR과 NPV는 프로젝트가 상호 배타적 일 때 항상 동일한 결정으로 이어지지는 않습니다.
Mutually exclusive projects하나의 프로젝트를 선택하면 다른 프로젝트를 수락 할 수 없습니다. 비교중인 프로젝트가 상호 배타적 인 경우 NPV와 IRR간에 순위 충돌이 발생할 수 있습니다. 프로젝트 A와 프로젝트 B 중 하나를 선택해야하는 경우 NPV는 프로젝트 A의 수락을 제안 할 수 있지만 IRR은 프로젝트 B를 제안 할 수 있습니다.
NPV와 IRR 간의 이러한 유형의 충돌은 다음 이유 중 하나로 인해 발생할 수 있습니다.
- 프로젝트의 규모가 크게 다릅니다.
- 현금 흐름의 타이밍은 다릅니다.
크기 차이가 큰 프로젝트
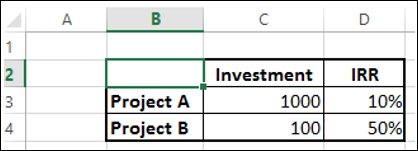
IRR에 의해 결정을 내리려는 경우 프로젝트 A는 100의 수익을, 프로젝트 B는 50의 수익을 얻습니다. 따라서 프로젝트 A에 대한 투자는 수익성이 높아 보입니다. 그러나 이것은 프로젝트 규모의 차이로 인해 잘못된 결정입니다.
고려-
투자 할 1000이 있습니다.
프로젝트 A에 전체 1000을 투자하면 100의 수익을 얻습니다.
프로젝트 B에 100을 투자하면 프로젝트 C와 같은 다른 프로젝트에 투자 할 수있는 900이 여전히 손에있을 것입니다. 프로젝트 C에 대해 20 %의 수익을 얻은 다음 프로젝트 B와 프로젝트 C에 대한 총 수익을 얻는다고 가정합니다. 230은 수익성이 훨씬 앞서 있습니다.
따라서 NPV는 이러한 경우 의사 결정을위한 더 나은 방법입니다.
현금 흐름 타이밍이 다른 프로젝트

다시 말하지만 IRR을 고려하여 결정한다면 프로젝트 B가 선택이 될 것입니다. 그러나 프로젝트 A는 NPV가 더 높고 이상적인 선택입니다.
불규칙한 간격의 현금 흐름 (XIRR)의 IRR
현금 흐름의 간격이 불규칙 할 수 있습니다. 이러한 경우 IRR에는 동일한 간격의 시간 간격이 필요하므로 IRR을 사용할 수 없습니다. 대신 현금 흐름과 함께 현금 흐름의 날짜를 고려하는 XIRR을 사용할 수 있습니다.

그 결과 내부 수익률은 26.42 %입니다.

수정 된 IRR (MIRR)
재정 비율이 재투자 비율과 다른 경우를 고려하십시오. IRR을 사용하여 내부 수익률을 계산하면 금융 및 재투자에 대해 동일한 비율을 가정합니다. 또한 여러 IRR을 얻을 수도 있습니다.
예를 들어, 아래에 주어진 현금 흐름을 고려하십시오.

보시다시피 NPV는 두 번 이상 0이므로 여러 IRR이 발생합니다. 또한 재 투자율은 고려되지 않습니다. 이러한 경우 MIRR (modified IRR)을 사용할 수 있습니다.

아래와 같이 7 %의 결과를 얻을 수 있습니다.

Note − IRR과 달리 MIRR은 항상 고유합니다.