Obwody cyfrowe - de-multipleksery
De-Multiplexerto układ kombinacyjny, który wykonuje odwrotną operację multipleksera. Posiada pojedyncze wejście, „n” linii wyboru i maksymalnie 2 n wyjść. Wejście zostanie podłączone do jednego z tych wyjść na podstawie wartości linii wyboru.
Ponieważ istnieje „n” linii wyboru, będzie 2 n możliwych kombinacji zer i jedynek. Tak więc każda kombinacja może wybrać tylko jedno wyjście. De-multiplekser jest również nazywany jakoDe-Mux.
De-multiplekser 1x4
De-multiplekser 1x4 ma jedno wejście I, dwie linie wyboru, s 1 i s 0 oraz cztery wyjścia Y 3 , Y 2 , Y 1 i Y 0 . Plikblock diagram demultipleksera 1x4 pokazano na poniższym rysunku.

Pojedyncze wejście „I” zostanie podłączone do jednego z czterech wyjść od Y 3 do Y 0 na podstawie wartości linii wyboru s 1 i s0. PlikTruth table demultipleksera 1x4 pokazano poniżej.
| Wybór wejść | Wyjścia | ||||
|---|---|---|---|---|---|
| S1 | S0 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | I |
| 0 | 1 | 0 | 0 | I | 0 |
| 1 | 0 | 0 | I | 0 | 0 |
| 1 | 1 | I | 0 | 0 | 0 |
Z powyższej tabeli Prawdy możemy bezpośrednio napisać plik Boolean functions dla każdego wyjścia jako
$$ Y_ {3} = s_ {1} s_ {0} I $$
$$ Y_ {2} = s_ {1} {s_ {0}} 'I $$
$$ Y_ {1} = {s_ {1} }'s_ {0} I $$
$$ Y_ {0} = {s_1} '{s_ {0}}' I $$
Możemy zaimplementować te funkcje logiczne za pomocą falowników i 3-wejściowych bramek AND. Plikcircuit diagram demultipleksera 1x4 pokazano na poniższym rysunku.

Z łatwością możemy zrozumieć działanie powyższego obwodu. Podobnie można zaimplementować de-multiplekser 1x8 i de-multiplekser 1x16, wykonując tę samą procedurę.
Implementacja demultiplekserów wyższego rzędu
Teraz zaimplementujmy następujące dwa demultipleksery wyższego rzędu przy użyciu demultiplekserów niższego rzędu.
- De-multiplekser 1x8
- De-multiplekser 1x16
De-multiplekser 1x8
W tej sekcji zaimplementujmy demultiplekser 1x8 przy użyciu demultipleksera 1x4 i demultipleksera 1x2. Wiemy, że demultiplekser 1x4 ma jedno wejście, dwie linie wyboru i cztery wyjścia. Natomiast demultiplekser 1x8 ma jedno wejście, trzy linie wyboru i osiem wyjść.
Więc potrzebujemy dwóch 1x4 De-Multiplexersw drugim etapie, aby uzyskać ostatnie osiem wyników. Ponieważ liczba wejść w drugim etapie wynosi dwa, wymagamy1x2 DeMultiplexerw pierwszym etapie tak, aby wyjścia pierwszego etapu były wejściami drugiego etapu. Wejście tego demultipleksera 1x2 będzie ogólnym wejściem demultipleksera 1x8.
Niech demultiplekser 1x8 ma jedno wejście I, trzy linie wyboru s 2 , s 1 i s 0 oraz wyjścia Y 7 do Y 0 . PlikTruth table demultipleksera 1x8 pokazano poniżej.
| Wybór wejść | Wyjścia | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| s2 | s1 | s0 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | I |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | I | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Możemy łatwo wdrożyć demultiplekser 1x8 przy użyciu multiplekserów niższego rzędu, biorąc pod uwagę powyższą tabelę prawdy. Plikblock diagram demultipleksera 1x8 pokazano na poniższym rysunku.

Wspólne selection lines, s1 & s0są stosowane do obu de-multiplekserów 1x4. Wyjścia górnego demultipleksera 1x4 to Y 7 do Y 4, a wyjścia dolnego demultipleksera 1x4 to Y 3 do Y 0 .
Inny selection line, s2jest stosowany do De-multipleksera 1x2. Jeśli s 2 jest równe zero, to jedno z czterech wyjść dolnego demultipleksera 1x4 będzie równe wejściu, I na podstawie wartości linii wyboru s 1 i s 0 . Podobnie, jeśli s 2 wynosi jeden, to jedno z czterech wyjść górnego DeMultiplexera 1x4 będzie równe wejściu, I na podstawie wartości linii wyboru s 1 i s 0 .
De-multiplekser 1x16
W tej sekcji zaimplementujmy demultiplekser 1x16 przy użyciu de-multiplekserów 1x8 i de-multiplekserów 1x2. Wiemy, że demultiplekser 1x8 ma jedno wejście, trzy linie wyboru i osiem wyjść. Natomiast demultiplekser 1x16 ma pojedyncze wejście, cztery linie wyboru i szesnaście wyjść.
Więc potrzebujemy dwóch 1x8 De-Multiplexersw drugim etapie w celu uzyskania ostatnich szesnastu wyników. Ponieważ liczba wejść w drugim etapie wynosi dwa, wymagamy1x2 DeMultiplexerw pierwszym etapie tak, aby wyjścia pierwszego etapu były wejściami drugiego etapu. Wejście tego demultipleksera 1x2 będzie ogólnym wejściem demultipleksera 1x16.
Niech demultiplekser 1x16 ma jedno wejście I, cztery linie wyboru s 3 , s 2 , s 1 i s 0 oraz wyjścia Y 15 do Y 0 . Plikblock diagram demultipleksera 1x16 przy użyciu multiplekserów niższego rzędu pokazano na poniższym rysunku.
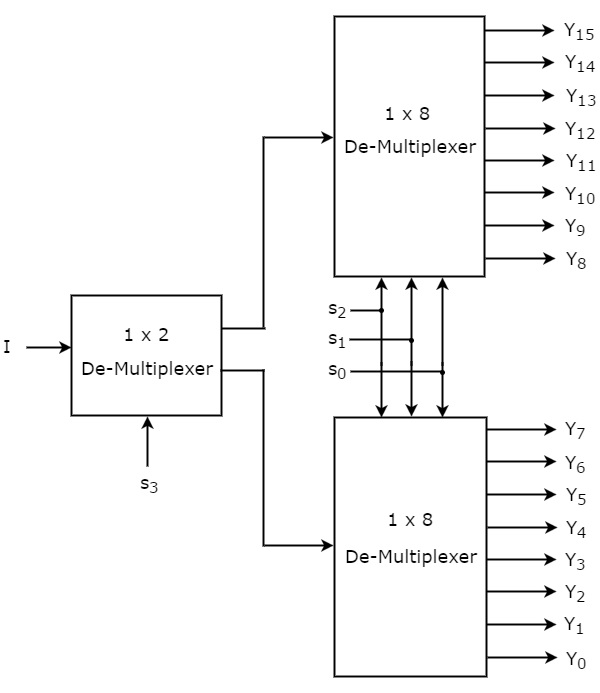
Wspólne selection lines s2, s1 & s0są stosowane do obu de-multiplekserów 1x8. Wyjścia górnego demultipleksera 1x8 to Y 15 do Y 8, a wyjścia dolnego demultipleksera 1x8 to Y 7 do Y 0 .
Inny selection line, s3jest stosowany do De-multipleksera 1x2. Jeśli s 3 wynosi zero, to jedno z ośmiu wyjść dolnego demultipleksera 1x8 będzie równe wejściu, I na podstawie wartości linii wyboru s 2 , s 1 i s 0 . Podobnie, jeśli s3 wynosi jeden, to jedno z 8 wyjść górnego demultipleksera 1x8 będzie równe wejściu, I na podstawie wartości linii wyboru s 2 , s 1 i s 0 .