Obwody cyfrowe - dwupoziomowa realizacja logiki

Maksymalna liczba poziomów występujących między wejściami a wyjściami to dwa cale two level logic. Oznacza to, że niezależnie od całkowitej liczby bramek logicznych, maksymalna liczba bramek logicznych, które są obecne (kaskadowo) między dowolnym wejściem i wyjściem, wynosi dwa w logice dwupoziomowej. Tutaj wyjścia bramek logicznych pierwszego poziomu są połączone jako wejścia bramek logicznych drugiego poziomu.

Rozważmy cztery bramki logiczne AND, OR, NAND i NOR. Ponieważ istnieją 4 bramki logiczne, otrzymamy 16 możliwych sposobów realizacji logiki dwupoziomowej. Są to AND-AND, AND-OR, ANDNAND, AND-NOR, OR-AND, OR-OR, OR-NAND, OR-NOR, NAND-AND, NAND-OR, NANDNAND, NAND-NOR, NOR-AND, NOR-OR, NOR-NAND, NOR-NOR.

Te dwupoziomowe realizacje logiczne można podzielić na następujące dwie kategorie.

• Forma zwyrodnieniowa
• Forma nie degeneracyjna

Forma zwyrodnieniowa

Jeśli wyjście dwupoziomowej realizacji logiki można uzyskać za pomocą pojedynczej bramki logicznej, wówczas nazywa się to as degenerative form. Oczywiście liczba wejść pojedynczej bramki logicznej wzrasta. Z tego powodu zwiększa się wachlowanie bramki logicznej. To zaleta zwyrodnieniowej formy.

Tylko 6 combinationsdwupoziomowych realizacji logicznych z 16 kombinacji ma postać degeneracyjną. Są to AND-AND, AND-NAND, OR-OR, OR-NOR, NAND-NOR, NORNAND.

W tej sekcji omówimy kilka realizacji. Załóżmy, że A, B, C i D to wejścia, a Y to wyjście w każdej realizacji logicznej.

Logika AND-AND

W tej logicznej realizacji bramki AND są obecne na obu poziomach. Poniższy rysunek przedstawia przykład dlaAND-AND logic realizacja.

Otrzymamy dane wyjściowe bramek logicznych pierwszego poziomu jako $ Y_ {1} = AB $ i $ Y_ {2} = CD $

Te wyjścia, $ Y_ {1} $ i $ Y_ {2} $ są stosowane jako wejścia bramki AND, która jest obecna na drugim poziomie. Zatem wyjście tej bramki AND to

$$ Y = Y_ {1} Y_ {2} $$

Zastąp wartości $ Y_ {1} $ i $ Y_ {2} $ w powyższym równaniu.

$$ Y = \ left (AB \ right) \ left (CD \ right) $$

$ \ Rightarrow Y = ABCD $

Dlatego wynikiem tej realizacji logiki AND-AND jest ABCD. Tę funkcję boolowską można zaimplementować za pomocą 4-wejściowej bramki AND. Dlatego tak jestdegenerative form.

Logika AND-NAND

W tej realizacji logiki bramki AND są obecne na pierwszym poziomie, a bramki NAND są obecne na drugim poziomie. Poniższy rysunek przedstawia przykład dlaAND-NAND logic realizacja.

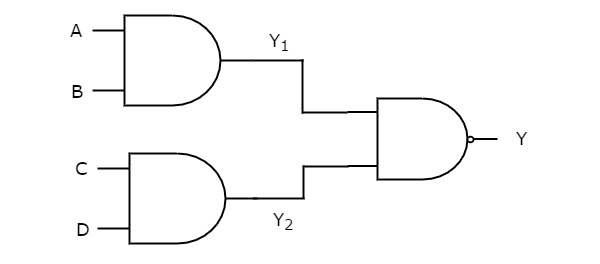
Wcześniej otrzymaliśmy dane wyjściowe bramek logicznych pierwszego poziomu jako $ Y_ {1} = AB $ i $ Y_ {2} = CD $

Te wyjścia, $ Y_ {1} $ i $ Y_ {2} $, są stosowane jako wejścia bramki NAND, która jest obecna na drugim poziomie. Tak więc wyjście tej bramki NAND to

$$ Y = {\ left (Y_ {1} Y_ {2} \ right)} '$$

Zastąp wartości $ Y_ {1} $ i $ Y_ {2} $ w powyższym równaniu.

$$ Y = {\ left (\ left (AB \ right) \ left (CD \ right) \ right)} '$$

$ \ Rightarrow Y = {\ left (ABCD \ right)} '$

Dlatego wyjście tej realizacji logiki AND-NAND to $ {\ left (ABCD \ right)} '$. Tę funkcję boolowską można zaimplementować za pomocą 4-wejściowej bramki NAND. Dlatego tak jestdegenerative form.

Logika OR-OR

W tej logicznej realizacji bramki OR są obecne na obu poziomach. Poniższy rysunek przedstawia przykład dlaOR-OR logic realizacja.

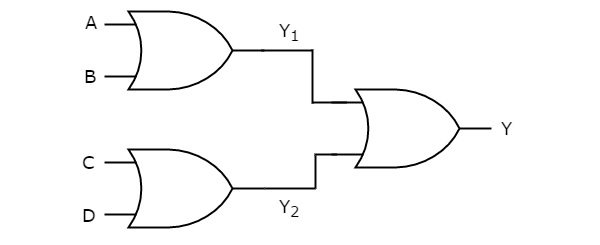
Otrzymamy dane wyjściowe bramek logicznych pierwszego poziomu jako $ Y_ {1} = A + B $ i $ Y_ {2} = C + D $.

Te wyjścia, $ Y_ {1} $ i $ Y_ {2} $ są stosowane jako wejścia bramki OR, która jest obecna na drugim poziomie. Tak więc wyjście tej bramki OR to

$$ Y = Y_ {1} + Y_ {2} $$

Zastąp wartości $ Y_ {1} $ i $ Y_ {2} $ w powyższym równaniu.

$$ Y = \ left (A + B \ right) + \ left (C + D \ right) $$

$ \ Rightarrow Y = A + B + C + D $

Dlatego wyjście tej realizacji logiki OR-OR jest A+B+C+D. Tę funkcję boolowską można zaimplementować za pomocą 4-wejściowej bramki LUB. Dlatego tak jestdegenerative form.

Podobnie możesz zweryfikować, czy pozostałe realizacje należą do tej kategorii, czy nie.

Forma nie-degeneracyjna

Jeśli wynik realizacji logiki dwupoziomowej nie może zostać uzyskany przy użyciu pojedynczej bramki logicznej, wówczas nazywa się to as non-degenerative form.

Pozostali 10 combinationslogiki dwupoziomowej mają postać niedegeneratywną. Są to AND-OR, AND-NOR, OR-AND, OR-NAND, NAND-AND, NANDOR, NAND-NAND, NOR-AND, NOR-OR, NOR-NOR.

Omówmy teraz kilka realizacji. Załóżmy, że A, B, C i D to wejścia, a Y to wyjście w każdej realizacji logicznej.

Logika AND-OR

W tej realizacji logiki bramki AND są obecne na pierwszym poziomie, a bramki OR są obecne na drugim poziomie. Poniższy rysunek przedstawia przykład dlaAND-OR logic realizacja.

Wcześniej otrzymaliśmy dane wyjściowe bramek logicznych pierwszego poziomu jako $ Y_ {1} = AB $ i $ Y_ {2} = CD $.

Te wyjścia, Y1 i Y2 są stosowane jako wejścia bramki OR, która jest obecna na drugim poziomie. Tak więc wyjście tej bramki OR to

$$ Y = Y_ {1} + Y_ {2} $$

Zastąp wartości $ Y_ {1} $ i $ Y_ {2} $ w powyższym równaniu

$$ Y = AB + CD $$

Dlatego wynikiem tej realizacji logiki AND-OR jest AB+CD. Ta funkcja boolowska jest wSum of ProductsFormularz. Ponieważ nie możemy tego zaimplementować przy użyciu pojedynczej bramki logicznej, ta realizacja logiki AND-OR tonon-degenerative form.

Logika AND-NOR

W tej realizacji logiki bramki AND są obecne na pierwszym poziomie, a bramki NOR są obecne na drugim poziomie. Poniższy rysunek przedstawia przykład dlaAND-NOR logic realizacja.

Znamy wyjścia bramek logicznych pierwszego poziomu jako $ Y_ {1} = AB $ i $ Y_ {2} = CD $

Te wyjścia, Y1 i Y2 są stosowane jako wejścia bramki NOR, która jest obecna na drugim poziomie. Zatem wyjście tej bramki NOR to

$$ Y = {\ left (Y_ {1} + Y_ {2} \ right)} '$$

Zastąp wartości $ Y_ {1} $ i $ Y_ {2} $ w powyższym równaniu.

$$ Y = {\ left (AB + CD \ right)} '$$

Dlatego wynikiem tej realizacji logiki AND-NOR jest $ {\ left (AB + CD \ right)} '$. Ta funkcja boolowska jest wAND-OR-InvertFormularz. Ponieważ nie możemy tego zaimplementować przy użyciu pojedynczej bramki logicznej, ta realizacja logiki AND-NOR tonon-degenerative form

Logika OR-AND

W tej realizacji logiki bramki OR są obecne na pierwszym poziomie, a bramki AND są obecne na drugim poziomie. Poniższy rysunek przedstawia przykład dlaOR-AND logic realizacja.

Wcześniej otrzymaliśmy dane wyjściowe bramek logicznych pierwszego poziomu jako $ Y_ {1} = A + B $ i $ Y_ {2} = C + D $.

Te wyjścia, $ Y_ {1} $ i $ Y_ {2} $ są stosowane jako wejścia bramki AND, która jest obecna na drugim poziomie. Zatem wyjście tej bramki AND to

$$ Y = Y_ {1} Y_ {2} $$

Zastąp wartości $ Y_ {1} $ i $ Y_ {2} $ w powyższym równaniu.

$$ Y = \ left (A + B \ right) \ left (C + D \ right) $$

Dlatego wynikiem tej realizacji logiki OR-AND jest (A + B) (C + D). Ta funkcja boolowska jest wProduct of SumsFormularz. Ponieważ nie możemy go zaimplementować przy użyciu pojedynczej bramki logicznej, ta realizacja logiki OR-AND tonon-degenerative form.

Podobnie możesz zweryfikować, czy pozostałe realizacje należą do tej kategorii, czy nie.