Obwody cyfrowe - logika progowa
W poprzednich rozdziałach zaimplementowaliśmy różne układy kombinacyjne wykorzystujące bramki logiczne. Z wyjątkiem bramki NOT, pozostałe wszystkie bramki logiczne mają co najmniej dwa wejścia i jedno wyjście. Podobniethreshold gate zawiera również co najmniej jedno wejście i tylko jedno wyjście.
Dodatkowo zawiera odpowiednie wagi dla każdego wejścia i wartość progową. Wartości tych wag i progów mogą mieć dowolną skończoną liczbę rzeczywistą.
Podstawy bramki progowej
Niech wejścia bramki progowej to X 1 , X 2 , X 3 ,…, X n . Odpowiednie wagi tych wejść to W 1 , W 2 , W 3 ,…, W n . Pliksymbol Bramki progowej pokazano na poniższym rysunku.
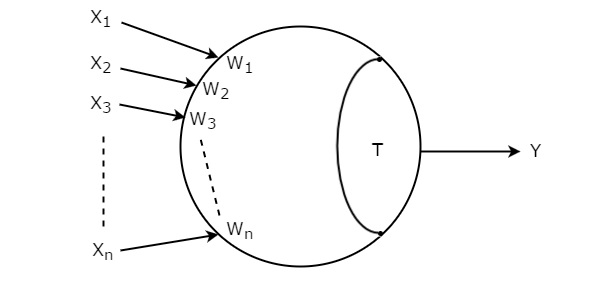
Threshold gatejest reprezentowany przez okrąg i ma wejścia 'n', X 1 do X n i pojedyncze wyjście, Y. Ten okrąg składa się z dwóch części. Jedna część przedstawia wagi odpowiadające wejściom, a druga część przedstawia wartość progową, T.
Suma iloczynów danych wejściowych z odpowiednimi wagami jest znana jako weighted sum. Jeśli ta ważona suma jest większa lub równa wartości progowej, T, wtedy tylko wyjście, Y będzie równe jeden. W przeciwnym razie wynik Y będzie równy zero.
Mathematically, możemy zapisać tę relację między wejściami i wyjściami bramki progowej, jak poniżej.
$$ Y = 1, jeśli \: \: W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {3} + ... W_ {n} X_ {n} \ geq T $$
= 0, w przeciwnym razie.
Dlatego możemy implementować różne bramki logiczne i funkcje boolowskie po prostu zmieniając wartości wag i / lub wartości progowej, T.
Przykład
Znajdźmy plik simplified Boolean function dla następnej bramki progowej.

Ta bramka progowa ma trzy wejścia X 1 , X 2 , X 3 i jedno wyjście Y.
Wagi odpowiadające wejściom X 1 , X 2 i X 3 wynoszą odpowiednio W 1 = 2, W 2 = 1 i W 3 = -4.
Wartość bramki progowej wynosi T = -1.
Plik weighted sum bramy progowej to
$$ W = W_ {1} X_ {1} + W_ {2} X_ {2} + W_ {3} X_ {3} $$
Zastąp podane wagi w powyższym równaniu.
$$ \ Rightarrow W = 2X_ {1} + X_ {2} -4X_ {3} $$
Wyjście bramki progowej, Y będzie wynosić „1”, jeśli W ≥ -1, w przeciwnym razie będzie to „0”.
Następujące table pokazuje relacje między wejściem i wyjściem dla wszystkich możliwych kombinacji wejść.
| Wejścia | Suma ważona | Wynik | ||
|---|---|---|---|---|
| $ X_ {1} $ | $ X_ {2} $ | $ X_ {3} $ | $ W = 2X_ {1} + X_ {2} -4X_ {3} $ | $ Y $ |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | -4 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | -3 | 0 |
| 1 | 0 | 0 | 2 | 1 |
| 1 | 0 | 1 | -2 | 0 |
| 1 | 1 | 0 | 3 | 1 |
| 1 | 1 | 1 | -1 | 1 |
Z powyższej tabeli możemy napisać plik Boolean function na wyjściu, Y jako
$$ Y = \ sum m \ left (0,2,4,6,7 \ right) $$
Uproszczenie tej funkcji logicznej przy użyciu 3 variable K-Map pokazano na poniższym rysunku.

Dlatego też simplified Boolean function dla danej bramki progowej to $ Y = {X_ {3} '} + X_ {1} X_ {2} $.
Synteza funkcji progowych
Brama progowa jest również nazywana jako universal gateponieważ możemy zaimplementować dowolną funkcję logiczną za pomocą bramek progowych. Czasami może nie być możliwe zaimplementowanie kilku bramek logicznych i funkcji boolowskich przy użyciu jednej bramki progowej. W takim przypadku możemy potrzebować wielu bramek progowych.
Postępuj zgodnie z tymi steps do implementacji funkcji logicznej przy użyciu pojedynczej bramki progowej.
Step 1 - Sformułuj a Truth table dla danej funkcji boolowskiej.
Step 2 - W powyższej tabeli Prawdy dodaj (uwzględnij) jeszcze jedną kolumnę, która podaje relację między weighted sums i Threshold value.
Step 3 - Napisz relację między sumami ważonymi a progiem dla każdej kombinacji danych wejściowych, jak wspomniano poniżej.
Jeśli wyjście funkcji boolowskiej wynosi 1, to suma ważona będzie większa lub równa wartości progowej dla tej kombinacji danych wejściowych.
Jeśli wynik funkcji boolowskiej wynosi 0, to suma ważona będzie mniejsza niż wartość progowa dla tej kombinacji danych wejściowych.
Step 4 - Dobierz wartości wag i progu w taki sposób, aby spełniały wszystkie relacje występujące w ostatniej kolumnie powyższej tabeli.
step 5 - Narysuj symbol bramki progowej z tymi wagami i wartością progową.
Przykład
Zaimplementujmy następujące Boolean function przy użyciu pojedynczej bramki progowej.
$$ Y \ left (X_ {1}, X_ {2}, X_ {3} \ right) = \ sum m \ left (0,2,4,6,7 \ right) $$
Podana funkcja boolowska jest funkcją z trzema zmiennymi, która jest reprezentowana jako suma minimalnych warunków. PlikTruth table tej funkcji pokazano poniżej.
| Wejścia | Wynik | ||
|---|---|---|---|
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Teraz dodajmy (uwzględnij) jeszcze jedną kolumnę do powyższej tabeli Prawdy. Ta ostatnia kolumna zawiera relacje międzyweighted sums (W) and Threshold wartość (T) dla każdej kombinacji wejść.
| Wejścia | Wynik | Relacje między W&T | ||
|---|---|---|---|---|
| X1 | X2 | X3 | Y | |
| 0 | 0 | 0 | 1 | 0 ≥ T. |
| 0 | 0 | 1 | 0 | W 3 <T |
| 0 | 1 | 0 | 1 | W 2 ≥ T |
| 0 | 1 | 1 | 0 | W 2 + W 3 <T |
| 1 | 0 | 0 | 1 | W 1 ≥ T |
| 1 | 0 | 1 | 0 | W 1 + W 3 <T |
| 1 | 1 | 0 | 1 | W 1 + W 2 ≥ T |
| 1 | 1 | 1 | 1 | W 1 + W 2 + W 3 ≥ T |
Poniżej przedstawiono wnioski z powyższej tabeli.
Wartość progu powinna być równa zero lub ujemna w oparciu o pierwszą relację.
Wartość W 3 powinna być ujemna na podstawie pierwszej i drugiej relacji.
Wartości W 1 i W 2 powinny być większe lub równe Wartość progowa na podstawie piątej i trzeciej relacji.
W 2 powinno być większe niż W 3 na podstawie czwartej zależności.
Na podstawie powyższych wniosków możemy wybrać następujące wartości wag i progu.
W 1 = 2, W 2 = 1, W 3 = -4 i T = -1
Plik symbol bramki progowej z powyższymi wartościami pokazano poniżej.

W związku z tym ta bramka progowa implementuje dane Boolean function, $ Y \ left (X_ {1}, X_ {2}, X_ {3} \ right) = \ sum m \ left (0,2,4,6,7 \ right) $.