Obwody cyfrowe - bramki logiczne
Cyfrowe układy elektroniczne działają z napięciami two logic levelsmianowicie Logic Low i Logic High. Zakres napięć odpowiadający poziomowi logiki niskiego jest oznaczony jako „0”. Podobnie, zakres napięć odpowiadający Logic High jest reprezentowany przez „1”.
Podstawowy cyfrowy obwód elektroniczny, który ma jedno lub więcej wejść i jedno wyjście, jest znany jako Logic gate. Dlatego bramki logiczne są elementami składowymi każdego systemu cyfrowego. Możemy podzielić te bramki logiczne na następujące trzy kategorie.
- Bramy podstawowe
- Bramy uniwersalne
- Bramy specjalne
Omówmy teraz, że bramki logiczne należą do każdej kategorii po kolei.
Podstawowe bramy
We wcześniejszych rozdziałach dowiedzieliśmy się, że funkcje boolowskie można przedstawić albo w postaci sumy iloczynów, albo w postaci iloczynu sum na podstawie wymagania. Tak więc możemy zaimplementować te funkcje boolowskie za pomocą podstawowych bramek. Podstawowe bramki to bramki AND, OR i NOT.
AND brama
Bramka AND to obwód cyfrowy, który ma dwa lub więcej wejść i generuje wyjście, którym jest logical ANDwszystkich tych danych wejściowych. Reprezentowanie plikuLogical AND z symbolem „.”.
W poniższej tabeli przedstawiono truth table 2-wejściowej bramki AND.
| ZA | b | Y = AB |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Tutaj A, B to wejścia, a Y to wyjście dwóch wejściowych bramek AND. Jeśli oba wejścia mają wartość „1”, to tylko wyjście, Y ma wartość „1”. W przypadku pozostałych kombinacji wejść wyjście Y wynosi „0”.
Poniższy rysunek przedstawia symbol bramki AND, która ma dwa wejścia A, B i jedno wyjście, Y.

Ta bramka AND generuje wyjście (Y), którym jest logical ANDdwóch wejść A, B. Podobnie, jeśli jest „n” wejść, wtedy bramka AND generuje wyjście, które jest logicznym AND wszystkich tych wejść. Oznacza to, że wyjście bramki AND będzie „1”, gdy wszystkie wejścia będą miały wartość „1”.
OR brama
Bramka OR to obwód cyfrowy, który ma dwa lub więcej wejść i generuje wyjście, które jest logicznym LUB wszystkich tych wejść. Tological OR jest reprezentowany przez symbol „+”.
W poniższej tabeli przedstawiono truth table 2-wejściowej bramki OR.
| ZA | b | Y = A + B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Tutaj A, B to wejścia, a Y to wyjście dwóch wejściowych bramek LUB. Jeśli oba wejścia mają wartość „0”, to tylko wyjście, Y ma wartość „0”. W przypadku pozostałych kombinacji wejść wyjście Y wynosi „1”.
Poniższy rysunek przedstawia symbol bramki OR, która ma dwa wejścia A, B i jedno wyjście, Y.

Ta bramka OR generuje wyjście (Y), którym jest logical ORdwóch wejść A, B. Podobnie, jeśli jest „n” wejść, wówczas bramka OR generuje wyjście, które jest logicznym OR wszystkich tych wejść. Oznacza to, że wyjście bramki OR będzie równe „1”, gdy przynajmniej jedno z tych wejść ma wartość „1”.
NIE brama
Bramka NOT to obwód cyfrowy, który ma jedno wejście i jedno wyjście. Wyjście NOT gate tological inversionwejścia. Dlatego bramka NOT jest również nazywana falownikiem.
W poniższej tabeli przedstawiono truth table NIE bramy.
| ZA | Y = A ' |
|---|---|
| 0 | 1 |
| 1 | 0 |
Tutaj A i Y są odpowiednio wejściem i wyjściem bramki NOT. Jeśli na wejściu A wynosi „0”, to na wyjściu Y wynosi „1”. Podobnie, jeśli wejście A wynosi „1”, to wyjście Y wynosi „0”.
Poniższy rysunek przedstawia symbol bramki NOT, która ma jedno wejście, A i jedno wyjście, Y.

Ta bramka NIE generuje wyjście (Y), którym jest complement wejścia, A.
Bramy uniwersalne
Bramki NAND i NOR nazywane są as universal gates. Ponieważ możemy zaimplementować dowolną funkcję boolowską, która jest sumą produktów przy użyciu samych bramek NAND. Podobnie możemy zaimplementować dowolną funkcję boolowską, która jest w postaci iloczynu sum przy użyciu samych bramek NOR.
Brama NAND
Bramka NAND to obwód cyfrowy, który ma dwa lub więcej wejść i wytwarza wyjście, którym jest inversion of logical AND wszystkich tych danych wejściowych.
W poniższej tabeli przedstawiono truth table 2-wejściowej bramki NAND.
| ZA | b | Y = (AB) ” |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Tutaj A, B to wejścia, a Y to wyjście dwóch wejściowych bramek NAND. Gdy oba wejścia mają wartość „1”, wyjście Y wynosi „0”. Jeśli co najmniej jedno z wejść ma wartość zero, to na wyjściu Y wynosi „1”. Jest to dokładnie odwrotne do działania z dwoma wejściami AND.
Poniższy obraz przedstawia symbol bramki NAND, która ma dwa wejścia A, B i jedno wyjście, Y.
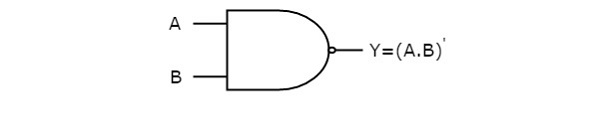
Działanie bramki NAND jest takie samo, jak w przypadku bramki AND, po której następuje falownik. Dlatego symbol bramki NAND jest reprezentowany w ten sposób.
Brama NOR
Bramka NOR jest obwodem cyfrowym, który ma dwa lub więcej wejść i wytwarza wyjście, którym jest inversion of logical OR wszystkich tych danych wejściowych.
W poniższej tabeli przedstawiono truth table 2-wejściowej bramki NOR
| ZA | b | Y = (A + B) ” |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Tutaj A, B to wejścia, a Y to wyjście. Jeśli oba wejścia mają wartość „0”, to na wyjściu Y wynosi „1”. Jeśli co najmniej jedno z wejść ma wartość „1”, to na wyjściu Y wynosi „0”. Jest to dokładnie odwrotne do działania z dwoma wejściami OR.
Poniższy rysunek przedstawia symbol bramki NOR, która ma dwa wejścia A, B i jedno wyjście, Y.

Działanie bramki NOR jest takie samo, jak w przypadku bramki OR, po której występuje falownik. Dlatego symbol bramki NOR jest reprezentowany w ten sposób.
Specjalne bramy
Bramy Ex-OR i Ex-NOR nazywane są bramkami specjalnymi. Ponieważ te dwie bramki są specjalnymi przypadkami bramek OR i NOR.
Brama Ex-OR
Pełna forma bramy Ex-OR to Exclusive-ORbrama. Jego funkcja jest taka sama jak bramki OR, z wyjątkiem niektórych przypadków, gdy wejścia mają parzystą liczbę jedynek.
W poniższej tabeli przedstawiono truth table 2-wejściowej bramki Ex-OR.
| ZA | b | Y = A⊕B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Tutaj A, B to wejścia, a Y to wyjście dwóch wejściowych bramek Ex-OR. Tabela prawdy bramki Ex-OR jest taka sama jak bramka OR dla pierwszych trzech wierszy. Jedyna modyfikacja znajduje się w czwartym rzędzie. Oznacza to, że wyjście (Y) wynosi zero zamiast jedynki, gdy oba wejścia są jednością, ponieważ wejścia mają parzystą liczbę jedynek.
Dlatego wyjście bramki Ex-OR to „1”, gdy tylko jedno z dwóch wejść ma wartość „1”. I wynosi zero, gdy oba wejścia są takie same.
Poniższy rysunek przedstawia symbol bramki Ex-OR, która ma dwa wejścia A, B i jedno wyjście Y.

Działanie bramki Ex-OR jest podobne do działania bramki OR, z wyjątkiem kilku kombinacji wejść. Dlatego symbol bramki Ex-OR jest reprezentowany w ten sposób. Wyjście bramki Ex-OR to '1', gdy na wejściach jest nieparzysta liczba jedynek. Stąd wyjście bramki Ex-OR jest również nazywane jako plikodd function.
Brama Ex-NOR
Pełna forma bramy Ex-NOR to Exclusive-NORbrama. Jego funkcja jest taka sama jak bramki NOR, z wyjątkiem niektórych przypadków, gdy wejścia mają parzystą liczbę jedynek.
W poniższej tabeli przedstawiono truth table 2-wejściowej bramki Ex-NOR.
| ZA | b | Y = A⊙B |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Tutaj A, B to wejścia, a Y to wyjście. Tabela prawdy dla bramki Ex-NOR jest taka sama jak dla bramki NOR dla pierwszych trzech wierszy. Jedyna modyfikacja znajduje się w czwartym rzędzie. Oznacza to, że wyjście ma wartość jeden zamiast zera, gdy oba wejścia są jednością.
Dlatego wyjście bramki Ex-NOR wynosi „1”, gdy oba wejścia są takie same. I wynosi zero, gdy oba wejścia są różne.
Poniższy rysunek przedstawia symbol bramki Ex-NOR, która ma dwa wejścia A, B i jedno wyjście Y.

Działanie bramki Ex-NOR jest podobne do działania bramki NOR, z wyjątkiem kilku kombinacji wejść. Dlatego symbol bramki Ex-NOR jest reprezentowany w ten sposób. Wyjście bramki Ex-NOR to „1”, gdy na wejściach jest parzysta liczba. Stąd wyjście bramki Ex-NOR jest również nazywane jako plikeven function.
Z powyższych tabel prawdy bramek logicznych Ex-OR i Ex-NOR można łatwo zauważyć, że operacja Ex-NOR jest tylko logiczną inwersją operacji Ex-OR.