Teorema de Convolução
No último tutorial, discutimos sobre as imagens no domínio da frequência. Neste tutorial, vamos definir uma relação entre o domínio da frequência e as imagens (domínio espacial).
Por exemplo
Considere este exemplo.

A mesma imagem no domínio da frequência pode ser representada como.

Agora, qual é a relação entre imagem ou domínio espacial e domínio da frequência. Esta relação pode ser explicada por um teorema que é chamado de teorema da convolução.
Teorema de Convolução
A relação entre o domínio espacial e o domínio da frequência pode ser estabelecida pelo teorema da convolução.
O teorema da convolução pode ser representado como.
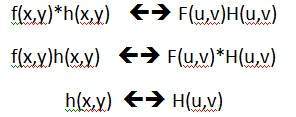
Pode-se afirmar que a convolução no domínio espacial é igual à filtragem no domínio da frequência e vice-versa.
A filtragem no domínio da frequência pode ser representada da seguinte forma:

The steps in filtering are given below.
Na primeira etapa temos que fazer um pré-processamento de uma imagem no domínio espacial, para aumentar seu contraste ou brilho
Em seguida, tomaremos a transformada discreta de Fourier da imagem
Em seguida, centralizaremos a transformada discreta de Fourier, pois traremos a transformada discreta de Fourier no centro dos cantos
Então vamos aplicar a filtragem, significa que vamos multiplicar a transformada de Fourier por uma função de filtro
Em seguida, iremos novamente deslocar o DFT do centro para os cantos
A última etapa seria realizar a transformada de Fourier discreta inversa, para trazer o resultado de volta do domínio da frequência para o domínio espacial
E essa etapa do pós-processamento é opcional, assim como o pré-processamento, no qual apenas aumentamos a aparência da imagem.
Filtros
O conceito de filtro no domínio da frequência é igual ao conceito de máscara na convolução.
Depois de converter uma imagem para o domínio da frequência, alguns filtros são aplicados no processo de filtragem para realizar diferentes tipos de processamento em uma imagem. O processamento inclui borrar uma imagem, aumentar a nitidez de uma imagem, etc.
Os tipos comuns de filtros para essas finalidades são:
- Filtro passa-alto ideal
- Filtro passa-baixo ideal
- Filtro passa-alto gaussiano
- Filtro passa-baixo gaussiano
No próximo tutorial, discutiremos sobre filtro em detalhes.