Transformação de nível de cinza

Discutimos algumas das transformações básicas em nosso tutorial de transformação básica. Neste tutorial, veremos algumas das transformações básicas de nível de cinza.

Melhoria de imagem

O aprimoramento de uma imagem fornece melhor contraste e uma imagem mais detalhada em comparação com a imagem não aprimorada. O aprimoramento de imagens tem muitas aplicações. É usado para aprimorar imagens médicas, imagens capturadas em sensoriamento remoto, imagens de satélite, etc.

A função de transformação foi dada abaixo

s = T (r)

onde r são os pixels da imagem de entrada es são os pixels da imagem de saída. T é uma função de transformação que mapeia cada valor de r para cada valor de s. O aprimoramento da imagem pode ser feito por meio de transformações de nível de cinza, que são discutidas abaixo.

Transformação de nível de cinza

Existem três transformações básicas de nível de cinza.

Linear
Logarithmic
Poder da lei

O gráfico geral dessas transições é mostrado abaixo.

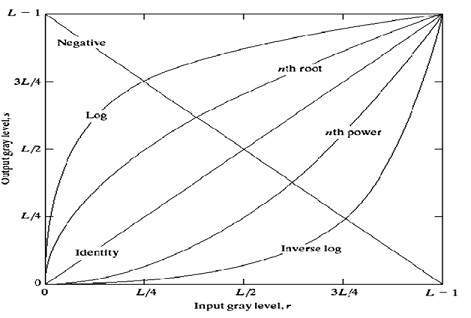
Transformação linear

Primeiro, veremos a transformação linear. A transformação linear inclui identidade simples e transformação negativa. A transformação de identidade foi discutida em nosso tutorial de transformação de imagem, mas uma breve descrição dessa transformação foi fornecida aqui.

A transição de identidade é mostrada por uma linha reta. Nesta transição, cada valor da imagem de entrada é diretamente mapeado para cada outro valor da imagem de saída. Isso resulta na mesma imagem de entrada e imagem de saída. E, portanto, é chamado de transformação de identidade. Foi mostrado abaixo:

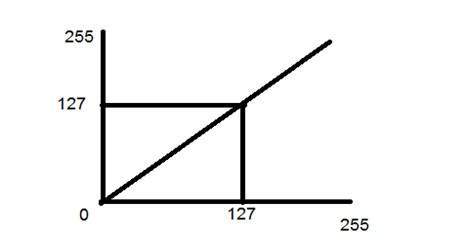
Transformação negativa

A segunda transformação linear é a transformação negativa, que é o inverso da transformação de identidade. Na transformação negativa, cada valor da imagem de entrada é subtraído de L-1 e mapeado na imagem de saída.

O resultado é mais ou menos assim.

Imagem de entrada

Imagem de saída

Neste caso, a seguinte transição foi feita.

s = (L - 1) - r

já que a imagem de entrada de Einstein é uma imagem de 8 bpp, então o número de níveis nesta imagem é 256. Colocando 256 na equação, obtemos isso

s = 255 - r

Portanto, cada valor é subtraído de 255 e a imagem resultante foi mostrada acima. Então o que acontece é que os pixels mais claros ficam escuros e a imagem mais escura fica clara. E isso resulta em imagem negativa.

Isso foi mostrado no gráfico abaixo.

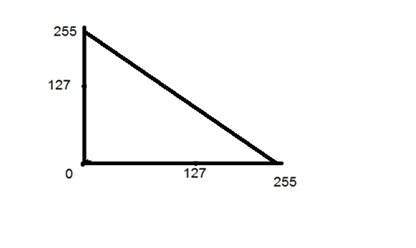
Transformações logarítmicas

A transformação logarítmica contém ainda dois tipos de transformação. Transformação de log e transformação de log inversa.

Transformação de log

As transformações de log podem ser definidas por esta fórmula

s = c log (r + 1).

Onde s e r são os valores de pixel da imagem de saída e de entrada e c é uma constante. O valor 1 é adicionado a cada um dos valores de pixel da imagem de entrada porque se houver uma intensidade de pixel de 0 na imagem, então log (0) é igual ao infinito. Portanto, 1 é adicionado, para tornar o valor mínimo de pelo menos 1.

Durante a transformação do log, os pixels escuros em uma imagem são expandidos em comparação com os valores de pixel mais altos. Os valores de pixel mais altos são comprimidos na transformação do log. Isso resulta no seguinte aprimoramento de imagem.

O valor de c na transformação do log ajusta o tipo de aprimoramento que você está procurando.

Imagem de entrada

Log Tranform Image

A transformação de log inversa é oposta à transformação de log.

Poder - transformações da lei

Existem mais duas transformações, as transformações de lei de potência, que incluem a enésima potência e a enésima transformação da raiz. Essas transformações podem ser dadas pela expressão:

s = cr ^ γ

Este símbolo γ é denominado gama, devido ao qual esta transformação também é conhecida como transformação gama.

A variação no valor de γ varia o realce das imagens. Dispositivos / monitores de exibição diferentes têm sua própria correção de gama, é por isso que exibem sua imagem em intensidades diferentes.

Esse tipo de transformação é usado para aprimorar imagens para diferentes tipos de dispositivos de exibição. A gama de diferentes dispositivos de exibição é diferente. Por exemplo, a gama de CRT está entre 1,8 e 2,5, o que significa que a imagem exibida no CRT está escura.