Transformação de perspectiva
Quando os olhos humanos veem coisas próximas, eles parecem maiores em comparação com aqueles que estão longe. Isso é chamado de perspectiva de uma maneira geral. Considerando que a transformação é a transferência de um objeto etc. de um estado para outro.
Portanto, no geral, a transformação da perspectiva trata da conversão do mundo 3D em imagem 2d. O mesmo princípio sobre o qual a visão humana funciona e o mesmo princípio sobre o qual a câmera funciona.
Veremos em detalhes por que isso acontece, que os objetos que estão perto de você parecem maiores, enquanto os que estão longe parecem menores, embora pareçam maiores quando você os alcança.
Começaremos esta discussão pelo conceito de quadro de referência:
Quadro de Referência:
O quadro de referência é basicamente um conjunto de valores em relação aos quais medimos algo.
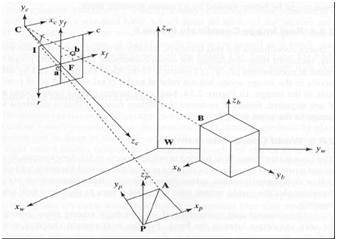
5 quadros de referência
Para analisar um mundo / imagem / cena 3D, 5 quadros de referência diferentes são necessários.
- Object
- World
- Camera
- Image
- Pixel
Quadro de coordenadas do objeto
O quadro de coordenadas do objeto é usado para modelar objetos. Por exemplo, verificar se um determinado objeto está em um local adequado em relação ao outro objeto. É um sistema de coordenadas 3D.
Quadro de coordenadas mundiais
O quadro de coordenadas do mundo é usado para co-relacionar objetos em um mundo tridimensional. É um sistema de coordenadas 3D.
Quadro de coordenadas da câmera
O quadro de coordenadas da câmera é usado para relacionar objetos em relação à câmera. É um sistema de coordenadas 3D.
Quadro de coordenadas da imagem
Não é um sistema de coordenadas 3D, mas sim um sistema 2D. É usado para descrever como os pontos 3D são mapeados em um plano de imagem 2d.
Quadro de coordenadas de pixel
É também um sistema de coordenadas 2d. Cada pixel tem um valor de coordenadas de pixel.
Transformação entre estes 5 frames

É assim que uma cena 3D se transforma em 2d, com imagem de pixels.
Agora vamos explicar esse conceito matematicamente.
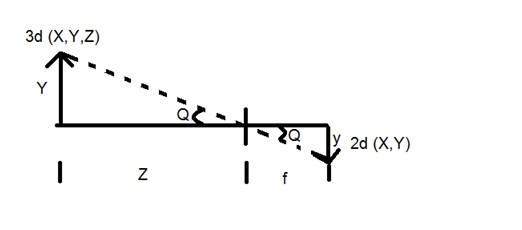
Onde
Y = objeto 3D
y = imagem 2d
f = comprimento focal da câmera
Z = distância entre o objeto e a câmera
Agora, existem dois ângulos diferentes formados nesta transformada, representados por Q.
O primeiro ângulo é
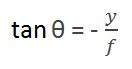
Onde menos denota que a imagem está invertida. O segundo ângulo que se forma é:

Comparando essas duas equações, obtemos

A partir dessa equação, podemos ver que quando os raios de luz refletem de volta após atingir o objeto, passado da câmera, uma imagem invertida é formada.
Podemos entender melhor isso, com este exemplo.
Por exemplo
Calculando o tamanho da imagem formada
Suponha que foi tirada uma imagem de uma pessoa de 5m de altura, e estando a uma distância de 50m da câmera, e temos que dizer que o tamanho da imagem da pessoa, com uma câmera de comprimento focal é de 50mm.
Solução:
Como a distância focal é em milímetros, temos que converter tudo em milímetros para podermos calculá-la.
Então,
Y = 5000 mm.
f = 50 mm.
Z = 50000 mm.
Colocando os valores na fórmula, obtemos
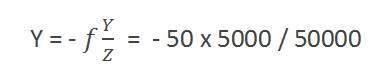
= -5 mm.
Novamente, o sinal de menos indica que a imagem está invertida.