DIP - Guia Rápido

Introdução

O processamento de sinais é uma disciplina da engenharia elétrica e da matemática que lida com a análise e o processamento de sinais analógicos e digitais e com o armazenamento, filtragem e outras operações em sinais. Esses sinais incluem sinais de transmissão, sinais de som ou voz, sinais de imagem e outros sinais, etc.

De todos esses sinais, o campo que trata do tipo de sinal para o qual a entrada é uma imagem e a saída também é uma imagem é feito no processamento de imagens. Como o próprio nome sugere, trata do processamento de imagens.

Ele pode ser dividido em processamento de imagem analógico e processamento de imagem digital.

Processamento analógico de imagem

O processamento analógico da imagem é feito em sinais analógicos. Inclui processamento em sinais analógicos bidimensionais. Nesse tipo de processamento, as imagens são manipuladas por meios elétricos, variando o sinal elétrico. O exemplo comum é a imagem da televisão.

O processamento de imagem digital tem dominado o processamento de imagem analógica com o passar do tempo devido à sua ampla gama de aplicações.

Processamento digital de imagens

O processamento digital de imagens trata do desenvolvimento de um sistema digital que realiza operações em uma imagem digital.

O que é uma imagem

Uma imagem nada mais é do que um sinal bidimensional. É definido pela função matemática f (x, y) onde xey são as duas coordenadas horizontal e verticalmente.

O valor de f (x, y) em qualquer ponto é o valor do pixel naquele ponto de uma imagem.

A figura acima é um exemplo de imagem digital que você está vendo agora na tela do computador. Mas, na verdade, esta imagem nada mais é do que uma matriz bidimensional de números variando entre 0 e 255.

128	30	123
232	123	321
123	77	89
80	255	255

Cada número representa o valor da função f (x, y) em qualquer ponto. Neste caso, o valor 128, 230, 123 cada um representa um valor de pixel individual. As dimensões da imagem são, na verdade, as dimensões dessa matriz bidimensional.

Relação entre uma imagem digital e um sinal

Se a imagem é uma matriz bidimensional, o que isso tem a ver com um sinal? Para entender isso, precisamos primeiro entender o que é um sinal?

Sinal

No mundo físico, qualquer quantidade mensurável através do tempo no espaço ou qualquer dimensão superior pode ser tomada como um sinal. Um sinal é uma função matemática e transmite algumas informações. Um sinal pode ser unidimensional ou bidimensional ou um sinal de dimensão superior. O sinal unidimensional é um sinal medido ao longo do tempo. O exemplo comum é um sinal de voz. Os sinais bidimensionais são aqueles medidos em outras quantidades físicas. O exemplo de sinal bidimensional é uma imagem digital. Veremos com mais detalhes no próximo tutorial como sinais unidimensionais ou bidimensionais e sinais superiores são formados e interpretados.

Relação

Pois qualquer coisa que transmita informações ou transmita uma mensagem no mundo físico entre dois observadores é um sinal. Isso inclui a fala ou (voz humana) ou uma imagem como um sinal. Desde quando falamos, nossa voz é convertida em onda / sinal sonora e transformada em relação ao tempo para a pessoa com quem estamos falando. Não só isso, mas a forma como uma câmera digital funciona, já que a aquisição de uma imagem de uma câmera digital envolve a transferência de um sinal de uma parte do sistema para outra.

Como uma imagem digital é formada

Já que capturar uma imagem de uma câmera é um processo físico. A luz solar é usada como fonte de energia. Uma matriz de sensores é usada para a aquisição da imagem. Portanto, quando a luz do sol incide sobre o objeto, a quantidade de luz refletida por esse objeto é detectada pelos sensores e um sinal de voltagem contínuo é gerado pela quantidade de dados detectados. Para criar uma imagem digital, precisamos converter esses dados em formato digital. Isso envolve amostragem e quantização. (Eles são discutidos mais tarde). O resultado da amostragem e quantização resulta em uma matriz bidimensional ou matriz de números que nada mais é do que uma imagem digital.

Campos sobrepostos

Visão de máquina / computador

A visão mecânica ou por computador trata do desenvolvimento de um sistema em que a entrada é uma imagem e a saída algumas informações. Por exemplo: Desenvolver um sistema que escaneia o rosto humano e abre qualquer tipo de fechadura. Este sistema seria mais ou menos assim.

Gráficos de computador

A computação gráfica lida com a formação de imagens a partir de modelos de objetos, em vez da imagem ser capturada por algum dispositivo. Por exemplo: Renderização de objetos. Gerando uma imagem a partir de um modelo de objeto. Esse sistema seria mais ou menos assim.

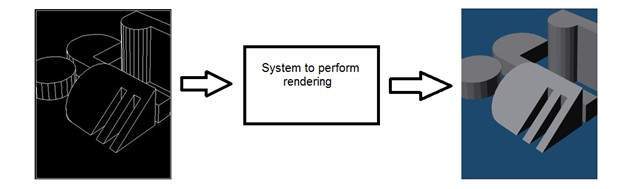
Inteligência artificial

A inteligência artificial é mais ou menos o estudo de colocar a inteligência humana em máquinas. A inteligência artificial tem muitas aplicações no processamento de imagens. Por exemplo: desenvolver sistemas de diagnóstico auxiliados por computador que auxiliem os médicos na interpretação de imagens de raios-X, ressonância magnética, etc. e, em seguida, destacando a seção visível a ser examinada pelo médico.

Processamento de sinal

O processamento de sinais é um guarda-chuva e o processamento de imagens está sob ele. A quantidade de luz refletida por um objeto no mundo físico (mundo 3D) passa pelas lentes da câmera e se torna um sinal 2d e, portanto, resulta na formação da imagem. Essa imagem é então digitalizada usando métodos de processamento de sinal e, em seguida, essa imagem digital é manipulada no processamento de imagem digital.

Este tutorial cobre os conceitos básicos de sinais e sistema necessários para a compreensão dos conceitos de processamento digital de imagens. Antes de entrar nos conceitos de detalhes, vamos primeiro definir os termos simples.

Sinais

Na engenharia elétrica, a quantidade fundamental de representação de algumas informações é chamada de sinal. Não importa quais são as informações, ou seja: Informações analógicas ou digitais. Em matemática, um sinal é uma função que transmite algumas informações. Na verdade, qualquer quantidade mensurável através do tempo no espaço ou qualquer dimensão superior pode ser tomada como um sinal. Um sinal pode ser de qualquer dimensão e pode ser de qualquer forma.

Sinais analógicos

Um sinal pode ser uma grandeza analógica, o que significa que é definido em relação ao tempo. É um sinal contínuo. Esses sinais são definidos em variáveis ​​independentes contínuas. Eles são difíceis de analisar, pois carregam um grande número de valores. Eles são muito precisos devido a uma grande amostra de valores. Para armazenar esses sinais, você precisa de uma memória infinita porque ela pode atingir valores infinitos em uma linha real. Os sinais analógicos são denotados por ondas sin.

Por exemplo:

Voz humana

A voz humana é um exemplo de sinais analógicos. Quando você fala, a voz produzida viaja pelo ar na forma de ondas de pressão e, portanto, pertence a uma função matemática, tendo variáveis ​​independentes de espaço e tempo e um valor correspondente à pressão do ar.

Outro exemplo é a onda sin que é mostrada na figura abaixo.

Y = sin (x) onde x é independente

Sinais digitais

Em comparação com os sinais analógicos, os sinais digitais são muito fáceis de analisar. Eles são sinais descontínuos. Eles são a apropriação de sinais analógicos.

A palavra digital significa valores discretos e, portanto, significa que eles usam valores específicos para representar qualquer informação. No sinal digital, apenas dois valores são usados ​​para representar algo, ou seja: 1 e 0 (valores binários). Os sinais digitais são menos precisos do que os sinais analógicos porque são amostras discretas de um sinal analógico obtido ao longo de algum período de tempo. No entanto, os sinais digitais não estão sujeitos a ruído. Portanto, eles duram muito e são fáceis de interpretar. Os sinais digitais são denotados por ondas quadradas.

Por exemplo:

Teclado de computador

Sempre que uma tecla é pressionada no teclado, o sinal elétrico apropriado é enviado ao controlador do teclado contendo o valor ASCII dessa tecla específica. Por exemplo, o sinal elétrico que é gerado quando a tecla a do teclado é pressionada, carrega informações do dígito 97 na forma de 0 e 1, que é o valor ASCII do caractere a.

Diferença entre sinais analógicos e digitais

Elemento de comparação	Sinal analógico	Sinal digital
Análise	Difícil	Possível analisar
Representação	Contínuo	Descontínuo
Precisão	Mais preciso	Menos preciso
Armazenamento	Memória infinita	Facilmente armazenado
Sujeito a ruído	sim	Não
Técnica de Gravação	O sinal original é preservado	Amostras do sinal são coletadas e preservadas
Exemplos	Voz humana, termômetro, telefones analógicos etc.	Computadores, telefones digitais, canetas digitais, etc.

Sistemas

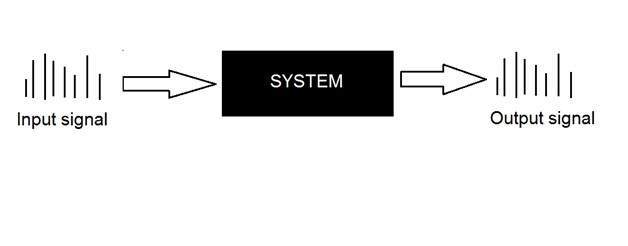
Um sistema é definido pelo tipo de entrada e saída com que lida. Já que estamos lidando com sinais, então, em nosso caso, nosso sistema seria um modelo matemático, um pedaço de código / software ou um dispositivo físico, ou uma caixa preta cuja entrada é um sinal e executa algum processamento nesse sinal, e a saída é um sinal. A entrada é conhecida como excitação e a saída como resposta.

Na figura acima, foi mostrado um sistema cuja entrada e saída são sinais, mas a entrada é um sinal analógico. E a saída é um sinal digital. Isso significa que nosso sistema é na verdade um sistema de conversão que converte sinais analógicos em sinais digitais.

Vamos dar uma olhada no interior deste sistema de caixa preta

Conversão de sinais analógicos em digitais

Uma vez que existem muitos conceitos relacionados a esta conversão de analógico para digital e vice-versa. Discutiremos apenas aqueles relacionados ao processamento digital de imagens. Existem dois conceitos principais que estão envolvidos na cobertura.

• Sampling

• Quantization

Amostragem

Amostragem, como o nome sugere, pode ser definido como obter amostras. Obtenha amostras de um sinal digital no eixo x. A amostragem é feita em uma variável independente. No caso desta equação matemática:

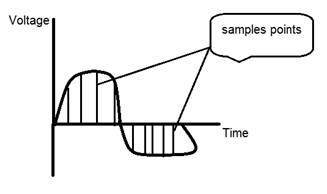
A amostragem é feita na variável x. Também podemos dizer que a conversão do eixo x (valores infinitos) para digital é feita sob amostragem.

A amostragem é ainda dividida em amostragem ascendente e amostragem inferior. Se a faixa de valores no eixo x for menor, então aumentaremos a amostra de valores. Isso é conhecido como up sampling e vice-versa é conhecido como down sampling

Quantização

Quantização, como o nome sugere, pode ser definida como divisão em quanta (partições). A quantização é feita na variável dependente. É o oposto da amostragem.

No caso desta equação matemática y = sin (x)

A quantização é feita na variável Y. Isso é feito no eixo y. A conversão dos valores infinitos do eixo y em 1, 0, -1 (ou qualquer outro nível) é conhecida como Quantização.

Estas são as duas etapas básicas envolvidas na conversão de um sinal analógico em um sinal digital.

A quantização de um sinal é mostrada na figura abaixo.

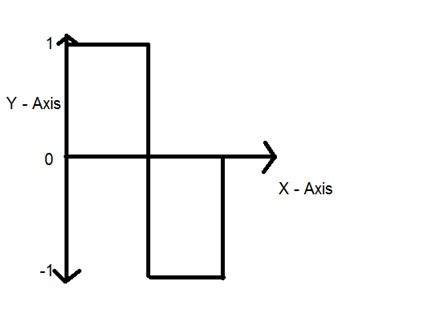
Por que precisamos converter um sinal analógico em sinal digital.

A primeira e óbvia razão é que o processamento digital de imagens lida com imagens digitais, que são sinais digitais. Assim, sempre que a imagem é capturada, ela é convertida em formato digital e, em seguida, é processada.

A segunda e importante razão é que, para realizar operações em um sinal analógico com um computador digital, você deve armazenar esse sinal analógico no computador. E para armazenar um sinal analógico, é necessária uma memória infinita para armazená-lo. E como isso não é possível, é por isso que convertemos esse sinal em formato digital e depois o armazenamos em um computador digital e então realizamos as operações nele.

Sistemas contínuos vs sistemas discretos

Sistemas contínuos

Os tipos de sistemas cujas entradas e saídas são sinais contínuos ou analógicos são chamados de sistemas contínuos.

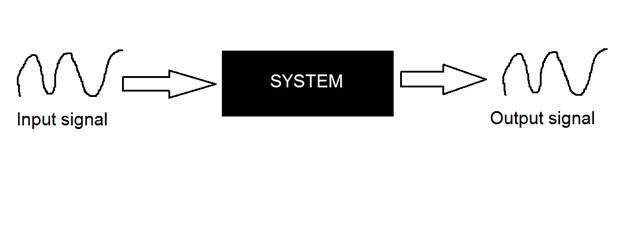
Sistemas discretos

O tipo de sistema cuja entrada e saída são sinais discretos ou digitais são chamados de sistemas digitais

Origem da câmera

A história da câmera e da fotografia não é exatamente a mesma. Os conceitos de câmera foram introduzidos muito antes do conceito de fotografia

Camera Obscura

A história da câmera está na ÁSIA. Os princípios da câmera foram introduzidos pela primeira vez por um filósofo chinês MOZI. É conhecido como câmera obscura. As câmeras evoluíram a partir desse princípio.

A palavra camera obscura evoluiu de duas palavras diferentes. Câmera e Obscura. O significado da palavra câmera é uma sala ou algum tipo de abóbada e Obscura significa escuro.

O conceito introduzido pelo filósofo chinês consiste em um dispositivo, que projeta uma imagem do seu entorno na parede. No entanto, não foi construído pelos chineses.

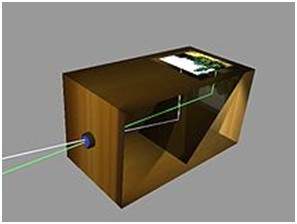
A criação da camera obscura

O conceito de chinês foi concretizado por um cientista muçulmano Abu Ali Al-Hassan Ibn al-Haitham comumente conhecido como Ibn al-Haitham. Ele construiu a primeira câmera obscura. Sua câmera segue os princípios da câmera pinhole. Ele construiu este dispositivo em algo em torno de 1000.

Camera portatil

Em 1685, uma primeira câmera portátil foi construída por Johann Zahn. Antes do advento deste dispositivo, as câmeras tinham o tamanho de uma sala e não eram portáteis. Embora um dispositivo tenha sido feito por um cientista irlandês Robert Boyle e Robert Hooke, era uma câmera transportável, mas ainda assim esse dispositivo era muito grande para carregá-la de um lugar para outro.

Origem da fotografia

Embora a câmera obscura tenha sido construída em 1000 por um cientista muçulmano. Mas seu primeiro uso real foi descrito no século 13 por um filósofo inglês Roger Bacon. Roger sugeriu o uso de câmera para a observação de eclipses solares.

Da Vinci

Embora muitas melhorias tenham sido feitas antes do século 15, as melhorias e as descobertas feitas por Leonardo di ser Piero da Vinci foram notáveis. Da Vinci foi um grande artista, músico, anatomista e engenheiro de guerra. Ele é creditado por muitas invenções. Sua uma das pinturas mais famosas inclui, a pintura de Mona Lisa.

Da vinci não só construiu uma câmera obscura seguindo o princípio de uma câmera pin hole, mas também a usa como auxílio de desenho para seu trabalho artístico. Em seu trabalho, que foi descrito no Codex Atlanticus, muitos princípios da camera obscura foram definidos.

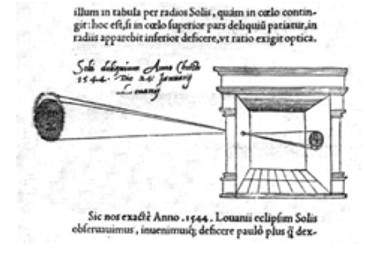
Sua câmera segue o princípio de uma câmera de orifício de alfinete, que pode ser descrita como

Quando imagens de objetos iluminados penetram por um pequeno orifício em uma sala muito escura, você verá [na parede oposta] esses objetos em sua forma e cor adequadas, reduzidos em tamanho na posição invertida, devido à interseção dos raios.

Primeira fotografia

A primeira fotografia foi tirada em 1814 pelo inventor francês Joseph Nicephore Niepce. Ele captura a primeira fotografia de uma vista da janela do Le Gras, revestindo a placa de estanho com betume e depois expondo essa placa à luz.

Primeira fotografia subaquática

A primeira fotografia subaquática foi tirada por um matemático inglês William Thomson usando uma caixa à prova d'água. Isso foi feito em 1856.

A origem do filme

A origem do cinema foi introduzida por um inventor e filantropo americano conhecido como George Eastman, considerado o pioneiro da fotografia.

Ele fundou a empresa Eastman Kodak, famosa por desenvolver filmes. A empresa começou a fabricar filme de papel em 1885. Ele primeiro criou a câmera Kodak e depois Brownie. Brownie era uma câmera box e ganhou sua popularidade devido ao seu recurso de Snapshot.

Após o advento do filme, a indústria de câmeras mais uma vez teve um boom e uma invenção levou a outra.

Leica e Argus

Leica e argus são as duas câmeras analógicas desenvolvidas em 1925 e 1939, respectivamente. A câmera Leica foi construída usando um filme cine 35mm.

Argus era outra câmera analógica que usa o formato 35mm e era bastante barata em comparação com a Leica e se tornou muito popular.

Câmeras analógicas de CFTV

Em 1942, um engenheiro alemão Walter Bruch desenvolveu e instalou o primeiro sistema de câmeras analógicas de CFTV. Ele também é creditado pela invenção da televisão em cores em 1960.

Photo Pac

A primeira câmera descartável foi lançada em 1949 pela Photo Pac. A câmera era apenas uma câmera de uso único com um rolo de filme já incluído. As versões posteriores do Photo pac eram à prova d'água e ainda tinham flash.

Câmeras digitais

Mavica da Sony

Mavica (a câmera de vídeo magnética) foi lançada pela Sony em 1981 foi a primeira virada de jogo no mundo das câmeras digitais. As imagens foram gravadas em disquetes e as imagens podem ser visualizadas posteriormente em qualquer tela do monitor.

Não era uma câmera digital pura, mas sim uma câmera analógica. Mas ganhou popularidade devido à sua capacidade de armazenamento de imagens em disquetes. Isso significa que agora você pode armazenar imagens por um longo período, e você pode salvar um grande número de imagens no disquete que são substituídas pelo novo disco em branco, quando ficam cheias. O Mavica tem capacidade para armazenar 25 imagens em disco.

Mais uma coisa importante que o mavica introduziu foi sua capacidade de 0,3 mega pixel de capturar fotos.

Câmeras digitais

Fuji DS-1P camera da Fuji films 1988 foi a primeira verdadeira câmera digital

Nikon D1 foi uma câmera de 2,74 megapixels e a primeira câmera SLR digital comercial desenvolvida pela Nikon, e era muito acessível para os profissionais.

Hoje, as câmeras digitais estão incluídas nos telefones celulares com resolução e qualidade muito altas.

Visto que o processamento de imagem digital tem aplicações muito amplas e quase todos os campos técnicos são afetados pelo DIP, discutiremos apenas algumas das principais aplicações do DIP.

O processamento digital de imagens não se limita apenas a ajustar a resolução espacial das imagens cotidianas capturadas pela câmera. Não se limita apenas a aumentar o brilho da foto, etc. Pelo contrário, é muito mais do que isso.

As ondas eletromagnéticas podem ser consideradas como um fluxo de partículas, em que cada partícula se move com a velocidade da luz. Cada partícula contém um feixe de energia. Esse feixe de energia é chamado de fóton.

O espectro eletromagnético de acordo com a energia do fóton é mostrado abaixo.

Neste espectro eletromagnético, somos capazes de ver apenas o espectro visível. O espectro visível inclui principalmente sete cores diferentes comumente denominadas como (VIBGOYR). VIBGOYR significa violeta, índigo, azul, verde, laranja, amarelo e vermelho.

Mas isso não anula a existência de outras coisas no espectro. Nosso olho humano só pode ver a parte visível, na qual vimos todos os objetos. Mas uma câmera pode ver outras coisas que a olho nu não consegue ver. Por exemplo: raios x, raios gama, etc. Portanto, a análise de tudo isso também é feita no processamento digital de imagens.

Esta discussão leva a outra questão que é

por que precisamos analisar todas as outras coisas no espectro EM também?

A resposta a esta pergunta está no fato, porque outras coisas como o XRay têm sido amplamente utilizadas no campo da medicina. A análise de raios gama é necessária porque é amplamente utilizado na medicina nuclear e observação astronômica. O mesmo acontece com o resto das coisas no espectro EM.

Aplicações de processamento digital de imagens

Alguns dos principais campos nos quais o processamento de imagem digital é amplamente utilizado são mencionados abaixo

• Nitidez e restauração de imagem

• Campo médico

• Sensoriamento remoto

• Transmissão e codificação

• Visão da máquina / robô

• Processamento de cor

• Reconhecimento de padrões

• Processamento de vídeo

• Imagem Microscópica

• Others

Nitidez e restauração de imagem

A nitidez e a restauração de imagem referem-se aqui a processar imagens que foram capturadas com a câmera moderna para torná-las uma imagem melhor ou para manipular essas imagens de forma a atingir o resultado desejado. Refere-se a fazer o que o Photoshop normalmente faz.

Isso inclui zoom, desfoque, nitidez, escala de cinza para conversão de cor, detecção de bordas e vice-versa, recuperação de imagem e reconhecimento de imagem. Os exemplos comuns são:

A imagem original

A imagem ampliada

Imagem borrada

Imagem nítida

Arestas

Campo médico

As aplicações comuns do DIP no campo da medicina são

1. Imagem de raios gama

2. PET scan

3. Imagem de raio x

4. CT Médica

5. Imagem UV

Imagem UV

No campo do sensoriamento remoto, a área da Terra é varrida por um satélite ou de um terreno muito elevado e, em seguida, é analisada para obter informações sobre ela. Uma aplicação particular do processamento digital de imagens no campo do sensoriamento remoto é a detecção de danos à infraestrutura causados ​​por um terremoto.

Como leva mais tempo para agarrar os danos, mesmo se houver danos graves. Visto que a área afetada pelo terremoto às vezes é tão grande, que não é possível examiná-la a olho nu para estimar os danos. Mesmo se for, é um procedimento muito agitado e demorado. Portanto, uma solução para isso é encontrada no processamento digital de imagens. Uma imagem da área afetada é capturada de cima do solo e, em seguida, é analisada para detectar os vários tipos de danos causados ​​pelo terremoto.

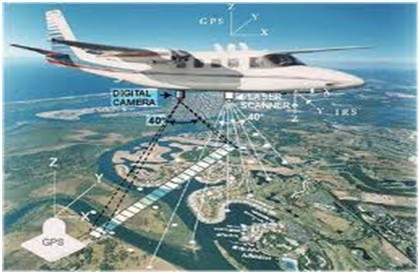
As principais etapas incluídas na análise são

1. A extração de bordas

2. Análise e aprimoramento de vários tipos de arestas

Transmissão e codificação

A primeira imagem transmitida por fio foi de Londres a Nova York por meio de um cabo submarino. A imagem enviada é mostrada abaixo.

A foto enviada demorou três horas para ir de um lugar a outro.

Agora, imagine que hoje podemos ver o feed de vídeo ao vivo ou imagens de cctv ao vivo de um continente para outro com apenas um atraso de segundos. Isso significa que muito trabalho foi feito também neste campo. Este campo não se concentra apenas na transmissão, mas também na codificação. Muitos formatos diferentes foram desenvolvidos para largura de banda alta ou baixa para codificar fotos e transmiti-las pela internet ou etc.

Visão da máquina / robô

Além dos muitos desafios que um robô enfrenta hoje, um dos maiores desafios ainda é aumentar a visão do robô. Torne o robô capaz de ver as coisas, identificá-las, identificar os obstáculos, etc. Muito trabalho foi contribuído por este campo e um outro campo completo de visão computacional foi introduzido para trabalhar nele.

Deteção de obstáculos

A detecção de obstáculos é uma das tarefas comuns que têm sido feitas por meio do processamento de imagens, identificando diferentes tipos de objetos na imagem e calculando a distância entre o robô e os obstáculos.

Robô seguidor de linha

A maioria dos robôs de hoje trabalha seguindo a linha e, portanto, são chamados de robôs seguidores de linha. Isso ajuda um robô a se mover em seu caminho e realizar algumas tarefas. Isso também foi alcançado por meio do processamento de imagem.

Processamento de cor

O processamento de cores inclui o processamento de imagens coloridas e diferentes espaços de cores usados. Por exemplo, modelo de cores RGB, YCbCr, HSV. Também envolve estudar a transmissão, armazenamento e codificação dessas imagens coloridas.

Reconhecimento de padrões

O reconhecimento de padrões envolve o estudo do processamento de imagens e de vários outros campos que incluem o aprendizado de máquina (um ramo da inteligência artificial). No reconhecimento de padrões, o processamento de imagem é usado para identificar os objetos em uma imagem e, em seguida, o aprendizado de máquina é usado para treinar o sistema para a mudança no padrão. O reconhecimento de padrões é usado no diagnóstico auxiliado por computador, reconhecimento de escrita, reconhecimento de imagens, etc.

Processamento de vídeo

Um vídeo nada mais é do que o movimento muito rápido das imagens. A qualidade do vídeo depende do número de quadros / imagens por minuto e da qualidade de cada quadro sendo usado. O processamento de vídeo envolve redução de ruído, aprimoramento de detalhes, detecção de movimento, conversão de taxa de quadros, conversão de proporção de aspecto, conversão de espaço de cores, etc.

Veremos este exemplo para entender o conceito de dimensão.

Considere que você tem um amigo que mora na lua e quer lhe enviar um presente no seu presente de aniversário. Ele perguntou sobre sua residência na terra. O único problema é que o serviço de correio na lua não entende o endereço alfabético, mas apenas as coordenadas numéricas. Então, como você envia a ele sua posição na terra?

É daí que vem o conceito de dimensões. As dimensões definem o número mínimo de pontos necessários para apontar uma posição de qualquer objeto específico dentro de um espaço.

Portanto, vamos voltar ao nosso exemplo novamente, no qual você deve enviar sua posição na Terra para seu amigo na lua. Você envia a ele três pares de coordenadas. O primeiro é denominado longitude, o segundo denominado latitude e o terceiro denominado altitude.

Essas três coordenadas definem sua posição na terra. Os dois primeiros definem sua localização e o terceiro define sua altura acima do nível do mar.

Isso significa que apenas três coordenadas são necessárias para definir sua posição na terra. Isso significa que você vive em um mundo que é tridimensional. E, portanto, isso não apenas responde à questão sobre a dimensão, mas também responde a razão pela qual vivemos em um mundo 3D.

Já que estamos estudando este conceito em referência ao processamento digital de imagens, vamos agora relacionar este conceito de dimensão com uma imagem.

Dimensões da imagem

Portanto, se vivemos no mundo 3D, significa um mundo tridimensional, quais são as dimensões de uma imagem que capturamos. Uma imagem é bidimensional, por isso também definimos uma imagem como um sinal bidimensional. Uma imagem tem apenas altura e largura. Uma imagem não tem profundidade. Basta dar uma olhada na imagem abaixo.

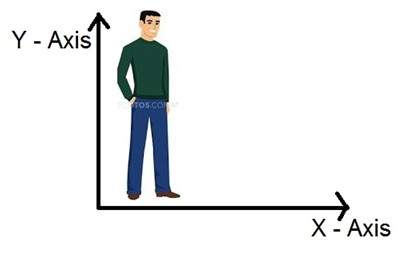
Se você olhar para a figura acima, verá que ela tem apenas dois eixos, que são os eixos de altura e largura. Você não pode perceber a profundidade desta imagem. É por isso que dizemos que uma imagem é um sinal bidimensional. Mas nosso olho é capaz de perceber objetos tridimensionais, mas isso seria mais explicado no próximo tutorial de como a câmera funciona e a imagem é percebida.

Esta discussão leva a algumas outras questões sobre como os sistemas de 3 dimensões são formados a partir de 2 dimensões.

Como funciona a televisão?

Se olharmos a imagem acima, veremos que é uma imagem bidimensional. Para convertê-lo em três dimensões, precisamos de uma outra dimensão. Vamos levar um tempo como a terceira dimensão, nesse caso vamos mover esta imagem bidimensional sobre o tempo da terceira dimensão. O mesmo conceito que acontece na televisão, que nos ajuda a perceber a profundidade de diferentes objetos em uma tela. Isso significa que o que aparece na TV ou o que vemos na tela da televisão é 3D? Bem, podemos sim. A razão é que, no caso da TV, se estamos reproduzindo um vídeo. Então, um vídeo nada mais é do que imagens bidimensionais que se movem ao longo da dimensão do tempo. Como objetos bidimensionais estão se movendo sobre a terceira dimensão, que é um tempo, podemos dizer que é tridimensional.

Diferentes dimensões de sinais

Sinal de 1 dimensão

O exemplo comum de um sinal de 1 dimensão é uma forma de onda. Pode ser representado matematicamente como

F (x) = forma de onda

Onde x é uma variável independente. Como é um sinal de uma dimensão, é por isso que há apenas uma variável x usada.

A representação pictórica de um sinal unidimensional é fornecida abaixo:

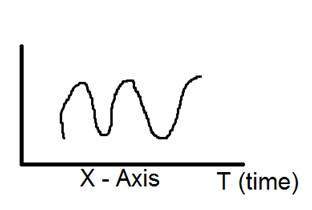
A figura acima mostra um sinal unidimensional.

Agora, isso leva a outra questão, que é, embora seja um sinal unidimensional, então por que ele tem dois eixos? A resposta a essa pergunta é que, embora seja um sinal unidimensional, estamos desenhando em um espaço bidimensional. Ou podemos dizer que o espaço no qual estamos representando esse sinal é bidimensional. É por isso que parece um sinal bidimensional.

Talvez você possa entender melhor o conceito de uma dimensão olhando para a figura abaixo.

Agora volte à nossa discussão inicial sobre dimensão. Considere a figura acima como uma linha real com números positivos de um ponto a outro. Agora, se tivermos que explicar a localização de qualquer ponto nesta linha, precisamos apenas de um número, o que significa apenas uma dimensão.

Sinal de 2 dimensões

O exemplo comum de um sinal bidimensional é uma imagem, que já foi discutida acima.

Como já vimos, uma imagem é um sinal bidimensional, ou seja: possui duas dimensões. Pode ser representado matematicamente como:

F (x, y) = imagem

Onde x e y são duas variáveis. O conceito de duas dimensões também pode ser explicado em termos matemáticos como:

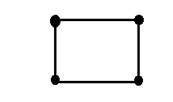
Agora na figura acima, rotule os quatro cantos do quadrado como A, B, C e D respectivamente. Se chamarmos, um segmento de linha na figura AB e o outro CD, então podemos ver que esses dois segmentos paralelos se unem e formam um quadrado. Cada segmento de linha corresponde a uma dimensão, portanto, esses dois segmentos de linha correspondem a 2 dimensões.

Sinal de 3 dimensões

Sinal tridimensional, como ele denomina, refere-se aos sinais que têm três dimensões. O exemplo mais comum foi discutido no início, que é o nosso mundo. Vivemos em um mundo tridimensional. Este exemplo foi discutido de forma muito elaborada. Outro exemplo de sinal tridimensional é um cubo ou dados volumétricos ou o exemplo mais comum seria um personagem animado ou de desenho animado 3D.

A representação matemática do sinal tridimensional é:

F (x, y, z) = personagem animado.

Outro eixo ou dimensão Z está envolvido em uma dimensão tridimensional, o que dá a ilusão de profundidade. Em um sistema de coordenadas cartesianas, pode ser visto como:

Sinal de 4 dimensões

Em um sinal de quatro dimensões, quatro dimensões estão envolvidas. Os três primeiros são iguais aos de um sinal tridimensional que são: (X, Y, Z), e o quarto que é adicionado a eles é T (tempo). O tempo é frequentemente referido como dimensão temporal, que é uma forma de medir a mudança. Matematicamente, um sinal de quatro d pode ser declarado como:

F (x, y, z, t) = filme animado.

O exemplo comum de um sinal quadridimensional pode ser um filme 3D animado. Como cada personagem é um personagem 3D e depois eles são movidos com relação ao tempo, devido ao que vimos uma ilusão de um filme tridimensional mais parecido com um mundo real.

Isso significa que, na realidade, os filmes animados são 4 dimensionais, ou seja: movimento de personagens 3D ao longo do tempo da quarta dimensão.

Como funciona o olho humano?

Antes de discutirmos a formação da imagem em câmeras analógicas e digitais, devemos primeiro discutir a formação da imagem no olho humano. Como o princípio básico seguido pelas câmeras foi retirado do caminho, o olho humano funciona.

Quando a luz incide sobre um objeto específico, ela é refletida de volta após atingir o objeto. Os raios de luz, quando passam pelas lentes do olho, formam um ângulo específico, e a imagem é formada na retina, que fica na parte de trás da parede. A imagem formada é invertida. Essa imagem é então interpretada pelo cérebro e isso nos torna capazes de entender as coisas. Devido à formação do ângulo, somos capazes de perceber a altura e profundidade do objeto que estamos vendo. Isso foi mais explicado no tutorial de transformação de perspectiva.

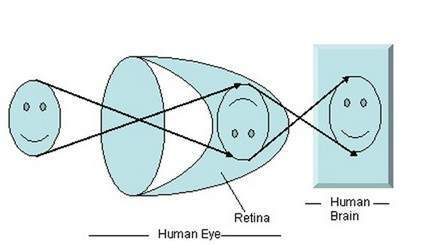
Como você pode ver na figura acima, quando a luz do sol incide sobre o objeto (neste caso, o objeto é um rosto), ela é refletida de volta e diferentes raios formam diferentes ângulos quando são passados ​​através da lente e uma imagem invertida de o objeto foi formado na parede posterior. A última parte da figura denota que o objeto foi interpretado pelo cérebro e reinvertido.

Agora vamos levar nossa discussão de volta à formação da imagem em câmeras analógicas e digitais.

Formação de imagem em câmeras analógicas

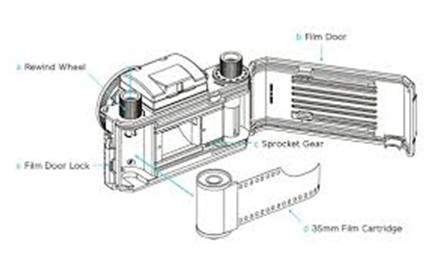
Em câmeras analógicas, a formação da imagem se deve à reação química que ocorre na tira que é usada para a formação da imagem.

Uma tira de 35 mm é usada na câmera analógica. É denotado na figura por um cartucho de filme de 35 mm. Esta tira é revestida com haleto de prata (uma substância química).

Uma tira de 35 mm é usada na câmera analógica. É denotado na figura por um cartucho de filme de 35 mm. Esta tira é revestida com haleto de prata (uma substância química).

A luz nada mais é do que pequenas partículas conhecidas como partículas de fótons. Então, quando essas partículas de fótons são passadas pela câmera, ela reage com as partículas de haleto de prata na tira e resulta na prata, que é o negativo da imagem.

Para entender melhor, dê uma olhada nesta equação.

Fótons (partículas de luz) + haleto de prata? prata ? negativo da imagem.

Este é apenas o básico, embora a formação da imagem envolva muitos outros conceitos relacionados à passagem da luz por dentro, e os conceitos de obturador e velocidade do obturador e abertura e sua abertura, mas por agora iremos passar para a próxima parte. Embora a maioria desses conceitos tenha sido discutida em nosso tutorial de obturador e abertura.

Este é apenas o básico, embora a formação da imagem envolva muitos outros conceitos relacionados à passagem da luz por dentro, e os conceitos de obturador e velocidade do obturador e abertura e sua abertura, mas por agora iremos passar para a próxima parte. Embora a maioria desses conceitos tenha sido discutida em nosso tutorial de obturador e abertura.

Formação de imagem em câmeras digitais

Nas câmeras digitais, a formação da imagem não se deve à reação química que ocorre, mas é um pouco mais complexa que isso. Na câmera digital, um conjunto CCD de sensores é usado para a formação da imagem.

Formação de imagem por meio de matriz CCD

CCD significa dispositivo acoplado por carga. É um sensor de imagem e, como outros sensores, detecta os valores e os converte em um sinal elétrico. No caso do CCD, ele detecta a imagem e a converte em sinal elétrico, etc.

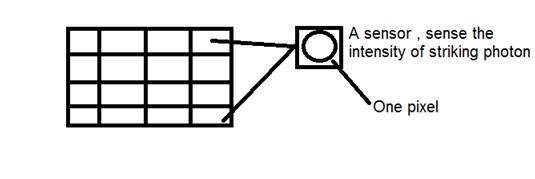
Na verdade, esse CCD tem o formato de uma matriz ou uma grade retangular. É como uma matriz, com cada célula da matriz contendo um censor que detecta a intensidade do fóton.

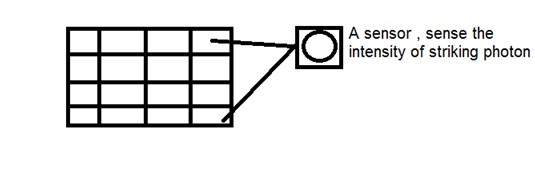
Assim como as câmeras analógicas, também no caso das digitais, quando a luz incide sobre o objeto, a luz reflete de volta após atingir o objeto e entrar no interior da câmera.

Cada sensor do próprio conjunto CCD é um sensor analógico. Quando os fótons de luz atingem o chip, ele é mantido como uma pequena carga elétrica em cada fotossensor. A resposta de cada sensor é diretamente igual à quantidade de luz ou energia (fóton) atingida na superfície do sensor.

Como já definimos uma imagem como um sinal bidimensional e devido à formação bidimensional da matriz CCD, uma imagem completa pode ser obtida a partir dessa matriz CCD.

Ele tem um número limitado de sensores e significa que um detalhe limitado pode ser capturado por ele. Além disso, cada sensor pode ter apenas um valor em relação a cada partícula de fóton que o atinge.

Assim, o número de fótons que atingem (atuais) são contados e armazenados. Para medi-los com precisão, os sensores CMOS externos também são acoplados ao conjunto CCD.

Introdução ao pixel

O valor de cada sensor da matriz CCD refere-se a cada um dos valores do pixel individual. O número de sensores = número de pixels. Isso também significa que cada sensor pode ter apenas um e apenas um valor.

Armazenando imagem

As cargas armazenadas pela matriz CCD são convertidas em voltagem, um pixel de cada vez. Com a ajuda de circuitos adicionais, essa tensão é convertida em uma informação digital e armazenada.

Cada empresa que fabrica câmeras digitais, faz seus próprios sensores CCD. Isso inclui Sony, Mistubishi, Nikon, Samsung, Toshiba, FujiFilm, Canon etc.

Além de outros fatores, a qualidade da imagem capturada também depende do tipo e da qualidade da matriz CCD utilizada.

Neste tutorial, discutiremos alguns dos conceitos básicos de câmera, como abertura, obturador, velocidade do obturador, ISO e discutiremos o uso coletivo desses conceitos para capturar uma boa imagem.

Abertura

A abertura é uma pequena abertura que permite que a luz entre na câmera. Aqui está a imagem da abertura.

Você verá algumas pequenas lâminas como coisas dentro da abertura. Essas lâminas criam uma forma octogonal que pode ser aberta e fechada. E, portanto, faz sentido que, quanto mais lâminas se abrirem, maior será o buraco pelo qual a luz teria que passar. Quanto maior for o buraco, mais luz pode entrar.

Efeito

O efeito da abertura corresponde diretamente ao brilho e escuridão de uma imagem. Se a abertura for ampla, permitirá que mais luz entre na câmera. Mais luz resultaria em mais fótons, o que acabaria resultando em uma imagem mais brilhante.

O exemplo disso é mostrado abaixo

Considere essas duas fotos

O do lado direito parece mais claro, isso significa que quando foi capturado pela câmera, a abertura estava totalmente aberta. Em comparação com a outra foto do lado esquerdo, que é muito escura em comparação com a primeira, isso mostra que quando aquela imagem foi capturada, sua abertura não estava totalmente aberta.

Tamanho

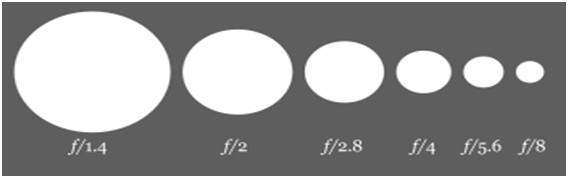
Agora vamos discutir a matemática por trás da abertura. O tamanho da abertura é denotado por um valor af. E é inversamente proporcional à abertura da abertura.

Aqui estão as duas equações que melhor explicam este conceito.

Tamanho de abertura grande = valor f pequeno

Tamanho da abertura pequena = maior valor f

De forma pictórica, pode ser representado como:

Obturador

Após a abertura, vem o obturador. A luz, quando pode passar pela abertura, incide diretamente sobre o obturador. O obturador é na verdade uma cobertura, uma janela fechada ou pode ser considerado uma cortina. Lembre-se de quando falamos sobre o sensor de matriz CCD no qual a imagem é formada. Bem atrás do obturador está o sensor. Portanto, o obturador é a única coisa que fica entre a formação da imagem e a luz, quando ela sai da abertura.

Assim que o obturador é aberto, a luz incide sobre o sensor de imagem e a imagem é formada na matriz.

Efeito

Se o obturador permitir que a luz passe um pouco mais, a imagem seria mais brilhante. Da mesma forma, uma imagem mais escura é produzida quando um obturador pode se mover muito rapidamente e, portanto, a luz que pode passar tem muito menos fótons, e a imagem que é formada no sensor de matriz CCD é muito escura.

O obturador tem mais dois conceitos principais:

• Velocidade do obturador

• Tempo do obturador

Velocidade do obturador

A velocidade do obturador pode ser referida como o número de vezes que o obturador abre ou fecha. Lembre-se de que não estamos falando sobre por quanto tempo a veneziana abre ou fecha.

Tempo do obturador

O tempo do obturador pode ser definido como

Quando o obturador está aberto, o tempo de espera que leva até que seja fechado é chamado de tempo do obturador.

Neste caso, não estamos falando sobre quantas vezes a veneziana abriu ou fechou, mas sim por quanto tempo ela permanece aberta.

Por exemplo:

Podemos entender melhor esses dois conceitos dessa forma. Isso quer dizer que uma veneziana abre 15 vezes e depois fecha, e para cada vez que abre por 1 segundo e depois fecha. Neste exemplo, 15 é a velocidade do obturador e 1 segundo é o tempo do obturador.

Relação

A relação entre a velocidade do obturador e o tempo do obturador é que ambos são inversamente proporcionais um ao outro.

Essa relação pode ser definida na equação abaixo.

Mais velocidade do obturador = menos tempo do obturador

Menos velocidade do obturador = mais tempo do obturador.

Explicação:

Quanto menor for o tempo necessário, maior será a velocidade. E quanto maior o tempo necessário, menor é a velocidade.

Formulários

Esses dois conceitos juntos formam uma variedade de aplicações. Alguns deles são fornecidos abaixo.

Objetos em movimento rápido:

Se você fosse capturar a imagem de um objeto em movimento rápido, poderia ser um carro ou qualquer coisa. O ajuste da velocidade do obturador e seu tempo afetaria muito.

Portanto, para capturar uma imagem como esta, faremos duas alterações:

• Aumentar a velocidade do obturador

• Diminuir o tempo do obturador

O que acontece é que, quando aumentamos a velocidade do obturador, quanto mais vezes, o obturador abre ou fecha. Significa que diferentes amostras de luz permitiriam a passagem. E quando diminuímos o tempo do obturador, significa que capturaremos imediatamente a cena e fecharemos o portão do obturador.

Se você fizer isso, terá uma imagem nítida de um objeto em movimento rápido.

Para entendê-lo, veremos este exemplo. Suponha que você queira capturar a imagem de uma queda d'água em movimento rápido.

Você define a velocidade do obturador para 1 segundo e tira uma foto. Isto é o que você recebe

Então você define a velocidade do obturador para uma velocidade mais rápida e você consegue.

Então, novamente, você define a velocidade do obturador para ainda mais rápida e você consegue.

Você pode ver na última foto que aumentamos a velocidade do obturador para muito rápido, o que significa que o obturador é aberto ou fechado em 200 de 1 segundo e, portanto, temos uma imagem nítida.

ISO

O fator ISO é medido em números. Isso denota a sensibilidade da luz à câmera. Se o número ISO for reduzido, significa que nossa câmera é menos sensível à luz e se o número ISO for alto, significa que é mais sensível.

Efeito

Quanto mais alto for o ISO, mais brilhante será a imagem. SE ISO estiver definido para 1600, a imagem ficará muito mais clara e vice-versa.

Efeito colateral

Se o ISO aumentar, o ruído na imagem também aumenta. Hoje, a maioria das empresas fabricantes de câmeras está trabalhando para remover o ruído da imagem quando o ISO é definido para uma velocidade mais alta.

Pixel

Pixel é o menor elemento de uma imagem. Cada pixel corresponde a qualquer valor. Em uma imagem em escala de cinza de 8 bits, o valor do pixel está entre 0 e 255. O valor de um pixel em qualquer ponto corresponde à intensidade dos fótons de luz que atingem aquele ponto. Cada pixel armazena um valor proporcional à intensidade da luz naquele local específico.

PEL

Um pixel também é conhecido como PEL. Você pode entender melhor o pixel nas imagens abaixo.

Na foto acima, pode haver milhares de pixels, que juntos formam esta imagem. Vamos ampliar essa imagem na medida em que formos capazes de ver algumas divisões de pixels. Isso é mostrado na imagem abaixo.

Na foto acima, pode haver milhares de pixels, que juntos formam esta imagem. Vamos ampliar essa imagem na medida em que formos capazes de ver algumas divisões de pixels. Isso é mostrado na imagem abaixo.

Relacionamento com matriz CCD

Vimos como uma imagem é formada na matriz CCD. Portanto, um pixel também pode ser definido como

A menor divisão da matriz CCD também é conhecida como pixel.

Cada divisão da matriz CCD contém o valor em relação à intensidade do fóton que a atinge. Este valor também pode ser chamado de pixel

Cálculo do número total de pixels

Definimos uma imagem como um sinal ou matriz bidimensional. Nesse caso, o número de PEL seria igual ao número de linhas multiplicado pelo número de colunas.

Isso pode ser representado matematicamente como abaixo:

Número total de pixels = número de linhas (X) número de colunas

Ou podemos dizer que o número de pares de coordenadas (x, y) compõe o número total de pixels.

Veremos com mais detalhes no tutorial de tipos de imagem, como calculamos os pixels em uma imagem colorida.

Nível de cinza

O valor do pixel em qualquer ponto denota a intensidade da imagem naquele local, e isso também é conhecido como nível de cinza.

Veremos com mais detalhes sobre o valor dos pixels no tutorial de armazenamento de imagens e bits por pixel, mas por enquanto vamos olhar apenas para o conceito de apenas um valor de pixel.

Valor do pixel. (0)

Como já foi definido no início deste tutorial, que cada pixel pode ter apenas um valor e cada valor denota a intensidade da luz naquele ponto da imagem.

Agora veremos um valor muito único 0. O valor 0 significa ausência de luz. Isso significa que 0 denota escuro e, além disso, significa que sempre que um pixel tem um valor de 0, significa que nesse ponto, a cor preta seria formada.

Dê uma olhada nesta matriz de imagem

0	0	0
0	0	0
0	0	0

Agora, esta matriz de imagem foi totalmente preenchida com 0. Todos os pixels têm um valor de 0. Se tivéssemos que calcular o número total de pixels desta matriz, é assim que o faremos.

Nº total de pixels = nº total. de linhas X total no. de colunas

= 3 X 3

= 9.

Isso significa que uma imagem seria formada com 9 pixels, e essa imagem teria uma dimensão de 3 linhas e 3 colunas e, o mais importante, essa imagem seria preta.

A imagem resultante que seria feita seria algo assim

Agora, por que essa imagem está toda preta. Porque todos os pixels da imagem têm valor 0.

Quando os olhos humanos veem as coisas de perto, eles parecem maiores em comparação com aqueles que estão longe. Isso é chamado de perspectiva de uma maneira geral. Considerando que a transformação é a transferência de um objeto etc. de um estado para outro.

Portanto, no geral, a transformação da perspectiva trata da conversão do mundo 3D em imagem 2d. O mesmo princípio sobre o qual a visão humana funciona e o mesmo princípio sobre o qual a câmera funciona.

Veremos em detalhes por que isso acontece, que os objetos que estão perto de você parecem maiores, enquanto os que estão longe parecem menores, embora pareçam maiores quando você os alcança.

Começaremos esta discussão pelo conceito de quadro de referência:

Quadro de Referência:

O quadro de referência é basicamente um conjunto de valores em relação aos quais medimos algo.

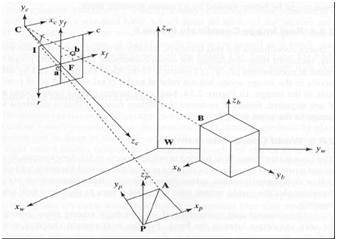
5 quadros de referência

Para analisar um mundo / imagem / cena 3D, são necessários 5 quadros de referência diferentes.

• Object

• World

• Camera

• Image

• Pixel

Quadro de coordenadas do objeto

O quadro de coordenadas do objeto é usado para modelar objetos. Por exemplo, verificar se um determinado objeto está em um local adequado em relação ao outro objeto. É um sistema de coordenadas 3D.

Quadro de coordenadas mundiais

O quadro de coordenadas do mundo é usado para co-relacionar objetos em um mundo tridimensional. É um sistema de coordenadas 3D.

Quadro de coordenadas da câmera

O quadro de coordenadas da câmera é usado para relacionar objetos em relação à câmera. É um sistema de coordenadas 3D.

Quadro de coordenadas da imagem

Não é um sistema de coordenadas 3D, mas sim um sistema 2D. É usado para descrever como os pontos 3D são mapeados em um plano de imagem 2d.

Quadro de coordenadas de pixel

É também um sistema de coordenadas 2d. Cada pixel tem um valor de coordenadas de pixel.

Transformação entre estes 5 frames

É assim que uma cena 3D se transforma em 2d, com imagem de pixels.

Agora vamos explicar esse conceito matematicamente.

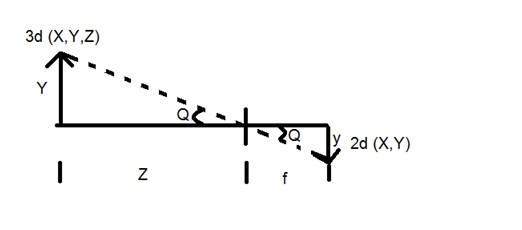
Y = objeto 3D

y = imagem 2d

f = comprimento focal da câmera

Z = distância entre a imagem e a câmera

Agora, existem dois ângulos diferentes formados nesta transformação que são representados por Q.

O primeiro ângulo é

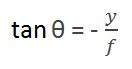
Onde menos denota que a imagem está invertida. O segundo ângulo que se forma é:

Comparando essas duas equações, obtemos

A partir dessa equação, podemos ver que quando os raios de luz refletem de volta após atingirem o objeto, passado da câmera, uma imagem invertida é formada.

Podemos entender melhor isso, com este exemplo.

Por exemplo

Calculando o tamanho da imagem formada

Suponha que foi tirada uma imagem de uma pessoa com 5m de altura, e em pé a uma distância de 50m da câmera, e temos que dizer que o tamanho da imagem da pessoa, com uma câmera de comprimento focal é de 50mm.

Solução:

Como a distância focal é em milímetros, temos que converter tudo em milímetros para podermos calculá-la.

Então,

Y = 5000 mm.

f = 50 mm.

Z = 50000 mm.

Colocando os valores na fórmula, obtemos

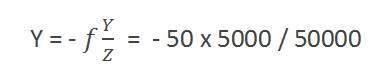
= -5 mm.

Novamente, o sinal de menos indica que a imagem está invertida.

Bpp ou bits por pixel denota o número de bits por pixel. O número de cores diferentes em uma imagem depende da profundidade da cor ou bits por pixel.

Bits em matemática:

É como brincar com bits binários.

Quantos números podem ser representados por um bit.

0

1

Quantas combinações de dois bits podem ser feitas.

00

01

10

11

Se criarmos uma fórmula para o cálculo do número total de combinações que podem ser feitas a partir do bit, seria assim.

Onde bpp denota bits por pixel. Coloque 1 na fórmula, você obtém 2, coloque 2 na fórmula, e você obtém 4. Ele cresce exponencialmente.

Número de cores diferentes:

Agora, como dissemos no início, que o número de cores diferentes depende do número de bits por pixel.

A tabela para alguns dos bits e suas cores é fornecida abaixo.

Bits por pixel	Número de cores
1 bpp	2 cores
2 bpp	4 cores
3 bpp	8 cores
4 bpp	16 cores
5 bpp	32 cores
6 bpp	64 cores
7 bpp	128 cores
8 bpp	256 cores
10 bpp	1024 cores
16 bpp	65536 cores
24 bpp	16777216 cores (16,7 milhões de cores)
32 bpp	4294967296 cores (4294 milhões de cores)

Esta tabela mostra diferentes bits por pixel e a quantidade de cor que eles contêm.

Tons

Você pode notar facilmente o padrão de crescimento exponencional. A famosa imagem em escala de cinza é de 8 bpp, o que significa que tem 256 cores diferentes ou 256 tons.

As sombras podem ser representadas como:

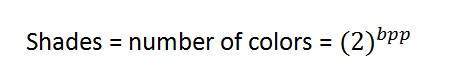
As imagens coloridas geralmente têm o formato de 24 bpp ou 16 bpp.

Veremos mais sobre outros formatos de cores e tipos de imagem no tutorial de tipos de imagem.

Valores de cor:

Cor preta:

Cor branca:

O valor que denota a cor branca pode ser calculado como:

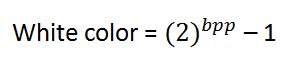
No caso de 1 bpp, 0 denota preto e 1 denota branco.

No caso de 8 bpp, 0 denota preto e 255 denota branco.

Cor cinza:

Ao calcular o valor da cor preta e branca, você pode calcular o valor do pixel da cor cinza.

A cor cinza é, na verdade, o ponto médio do preto e branco. Dito isto,

No caso de 8bpp, o valor do pixel que denota a cor cinza é 127 ou 128bpp (se você contar de 1, não de 0).

Requisitos de armazenamento de imagens

Após a discussão sobre bits por pixel, agora temos tudo o que precisamos para calcular o tamanho de uma imagem.

Tamanho da imagem

O tamanho de uma imagem depende de três coisas.

• Numero de linhas

• Numero de colunas

• Número de bits por pixel

A fórmula para calcular o tamanho é fornecida abaixo.

Tamanho de uma imagem = linhas * cols * bpp

Isso significa que se você tem uma imagem, digamos esta:

Supondo que ele tenha 1024 linhas e 1024 colunas. E como é uma imagem em escala de cinza, tem 256 tons diferentes de cinza ou bits por pixel. Então, colocando esses valores na fórmula, obtemos

Tamanho de uma imagem = linhas * cols * bpp

= 1024 * 1024 * 8

= 8388608 bits.

Mas, como não é uma resposta padrão que reconhecemos, vamos convertê-la em nosso formato.

Convertendo em bytes = 8388608/8 = 1048576 bytes.

Convertendo em bytes de kilo = 1048576/1024 = 1024 kb.

Convertendo em Mega bytes = 1024/1024 = 1 Mb.

É assim que o tamanho de uma imagem é calculado e armazenado. Agora, na fórmula, se você tiver o tamanho da imagem e os bits por pixel, também poderá calcular as linhas e colunas da imagem, desde que a imagem seja quadrada (mesmas linhas e mesma coluna).

Existem muitos tipos de imagens e veremos em detalhes sobre os diferentes tipos de imagens e a distribuição de cores nelas.

A imagem binária

A imagem binária, conforme seu nome indica, contém apenas dois valores de pixel.

0 e 1.

Em nosso tutorial anterior de bits por pixel, explicamos isso em detalhes sobre a representação dos valores de pixel em suas respectivas cores.

Aqui, 0 se refere à cor preta e 1 se refere à cor branca. Também é conhecido como Monocromático.

Imagem em preto e branco:

A imagem resultante formada, portanto, consiste apenas na cor preto e branco e, portanto, também pode ser chamada de imagem em preto e branco.

Sem nível de cinza

Uma das coisas interessantes sobre essa imagem binária é que não há nenhum nível de cinza nela. Apenas duas cores que são preto e branco são encontradas nele.

Formato

As imagens binárias têm um formato de PBM (mapa de bits portátil)

Formato de cores 2, 3, 4, 5, 6 bits

As imagens com formato de cor de 2, 3, 4, 5 e 6 bits não são muito utilizadas hoje. Eles foram usados ​​nos velhos tempos para telas de TV antigas ou monitores.

Mas cada uma dessas cores tem mais de dois níveis de cinza e, portanto, tem uma cor cinza ao contrário da imagem binária.

Em um 2 bit 4, em um 3 bit 8, em um 4 bit 16, em um 5 bit 32, em um 6 bit 64 cores diferentes estão presentes.

Formato de cor de 8 bits

O formato de cor de 8 bits é um dos formatos de imagem mais famosos. Possui 256 tons diferentes de cores. É comumente conhecido como imagem em tons de cinza.

A gama de cores em 8 bits varia de 0-255. Onde 0 significa preto, 255 significa branco e 127 significa cor cinza.

Esse formato foi usado inicialmente pelos primeiros modelos dos sistemas operacionais UNIX e pelos primeiros Macintoshes coloridos.

Uma imagem em tons de cinza de Einstein é mostrada abaixo:

Formato

O formato dessas imagens é PGM (Portable Gray Map).

Este formato não é suportado por padrão no Windows. Para ver imagens em escala de cinza, você precisa ter um visualizador de imagens ou uma caixa de ferramentas de processamento de imagem como o Matlab.

Por trás da imagem em escala de cinza:

Como explicamos várias vezes nos tutoriais anteriores, que uma imagem nada mais é que uma função bidimensional e pode ser representada por um array ou matriz bidimensional. Portanto, no caso da imagem de Einstein mostrada acima, haveria uma matriz bidimensional atrás com valores variando entre 0 e 255.

Mas esse não é o caso das imagens coloridas.

Formato de cor de 16 bits

É um formato de imagem colorida. Possui 65.536 cores diferentes. Também é conhecido como formato de alta cor.

Ele tem sido usado pela Microsoft em seus sistemas que oferecem suporte a formatos de cores de mais de 8 bits. Agora, neste formato de 16 bits e no próximo formato, vamos discutir que é um formato de 24 bits e ambos são formatos de cores.

A distribuição de cores em uma imagem colorida não é tão simples como era em uma imagem em tons de cinza.

Um formato de 16 bits é dividido em três formatos adicionais: Vermelho, Verde e Azul. O famoso formato (RGB).

Está representado pictoricamente na imagem abaixo.

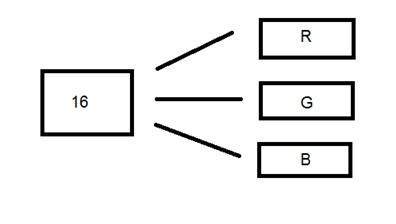
Agora surge a pergunta: como você distribuiria 16 em três. Se você fizer assim,

5 bits para R, 5 bits para G, 5 bits para B

Então, resta um bit no final.

Portanto, a distribuição de 16 bits foi feita assim.

5 bits para R, 6 bits para G, 5 bits para B.

O bit adicional que foi deixado para trás é adicionado ao bit verde. Porque o verde é a cor mais calmante para os olhos em todas essas três cores.

Observe que esta distribuição não é seguida por todos os sistemas. Alguns introduziram um canal alfa em 16 bits.

Outra distribuição de formato de 16 bits é a seguinte:

4 bits para R, 4 bits para G, 4 bits para B, 4 bits para canal alfa.

Ou alguns distribuem assim

5 bits para R, 5 bits para G, 5 bits para B, 1 bits para canal alfa.

Formato de cor de 24 bits

Formato de cor de 24 bits também conhecido como formato de cor verdadeira. Como o formato de cores de 16 bits, em um formato de cores de 24 bits, os 24 bits são novamente distribuídos em três formatos diferentes de vermelho, verde e azul.

Como 24 é dividido igualmente em 8, ele foi distribuído igualmente entre três canais de cores diferentes.

A distribuição deles é assim.

8 bits para R, 8 bits para G, 8 bits para B.

Atrás de uma imagem de 24 bits.

Ao contrário de uma imagem em escala de cinza de 8 bits, que tem uma matriz atrás dela, uma imagem de 24 bits tem três matrizes diferentes de R, G, B.

Formato

É o formato usado mais comum. Seu formato é PPM (Portable pixMap) que é compatível com o sistema operacional Linux. As famosas janelas têm seu próprio formato, que é o BMP (Bitmap).

Neste tutorial, veremos como diferentes códigos de cores podem ser combinados para fazer outras cores e como podemos converter códigos de cores RGB em hexadecimal e vice-versa.

Códigos de cores diferentes

Todas as cores aqui são do formato de 24 bits, o que significa que cada cor tem 8 bits de vermelho, 8 bits de verde e 8 bits de azul. Ou podemos dizer que cada cor tem três partes diferentes. Basta alterar a quantidade dessas três porções para fazer qualquer cor.

Formato de cor binária

Cor preta

Imagem:

Código decimal:

(0,0,0)

Explicação:

Como foi explicado nos tutoriais anteriores, em um formato de 8 bits, 0 se refere a preto. Portanto, se tivermos que fazer uma cor preta pura, temos que transformar todas as três partes de R, G, B em 0.

Cor branca

Imagem:

Código decimal:

(255.255.255)

Explicação:

Uma vez que cada porção de R, G, B é uma porção de 8 bits. Portanto, em 8 bits, a cor branca é formada por 255. Isso é explicado no tutorial do pixel. Então, para fazer uma cor branca, definimos cada porção em 255 e foi assim que obtivemos uma cor branca. Definindo cada um dos valores para 255, obtemos o valor geral de 255, o que torna a cor branca.

Modelo de cores RGB:

Cor vermelha

Imagem:

Código decimal:

(255,0,0)

Explicação:

Como precisamos apenas da cor vermelha, zeramos o restante das duas partes que são verdes e azuis e definimos a parte vermelha para seu máximo, que é 255.

Cor verde

Imagem:

Código decimal:

(0,255,0)

Explicação:

Como precisamos apenas da cor verde, zeramos o resto das duas partes que são vermelhas e azuis e definimos a parte verde para seu máximo, que é 255.

Cor azul

Imagem:

Código decimal:

(0,0,255)

Explicação:

Como precisamos apenas da cor azul, zeramos o restante das duas partes que são vermelhas e verdes e definimos a parte azul para o seu máximo, que é 255

Cor cinza:

Cor: Cinza

Imagem:

Código decimal:

(128.128.128)

Explicação:

Como já definimos em nosso tutorial de pixel, essa cor cinza é na verdade o ponto médio. Em um formato de 8 bits, o ponto médio é 128 ou 127. Neste caso, escolhemos 128. Portanto, configuramos cada parte em seu ponto médio, que é 128, e isso resulta em um valor médio geral e obtemos a cor cinza.

Modelo de cores CMYK:

CMYK é outro modelo de cor em que c significa ciano, m significa magenta, y significa amarelo ek significa preto. O modelo CMYK é comumente usado em impressoras coloridas em que dois cárteres de cor são usados. Um consiste em CMY e o outro na cor preta.

As cores do CMY também podem ser feitas alterando a quantidade ou porção de vermelho, verde e azul.

Cor: Ciano

Imagem:

Código decimal:

(0,255,255)

Explicação:

A cor ciano é formada pela combinação de duas cores diferentes, o verde e o azul. Portanto, definimos esses dois no máximo e zeramos a parte do vermelho. E obtemos a cor ciano.

Cor: Magenta

Imagem:

Código decimal:

(255.0.255)

Explicação:

A cor magenta é formada pela combinação de duas cores diferentes que são o vermelho e o azul. Portanto, definimos esses dois no máximo e zeramos a parte verde. E temos a cor magenta.

Cor amarela

Imagem:

Código decimal:

(255.255,0)

Explicação:

A cor amarela é formada a partir da combinação de duas cores diferentes, o vermelho e o verde. Portanto, definimos esses dois no máximo e zeramos a parte de azul. E temos a cor amarela.

Conversão

Agora veremos como as cores são convertidas de um formato para outro.

Conversão de RGB para código Hex:

A conversão de Hex em rgb é feita por meio deste método:

• Pegue uma cor. Ex: Branco = (255, 255, 255).

• Pegue a primeira porção, por exemplo, 255.

• Divida por 16. Assim:

• 

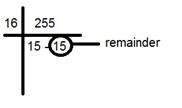
• Pegue os dois números abaixo da linha, o fator e o restante. Nesse caso, é 15 15 que é FF.

• Repita a etapa 2 para as próximas duas partes.

• Combine todo o código hexadecimal em um.

Resposta: #FFFFFF

Conversão de Hex para RGB:

A conversão do código hexadecimal para o formato decimal rgb é feita desta forma.

Pegue um número hexadecimal. Por exemplo: #FFFFFF

Divida este número em 3 partes: FF FF FF

Pegue a primeira parte e separe seus componentes: FF

Converta cada uma das partes separadamente em binário: (1111) (1111)

Agora combine os binários individuais em um: 11111111

Converta este binário em decimal: 255

Agora repita a etapa 2, mais duas vezes.

O valor que vem na primeira etapa é R, o segundo é G e o terceiro pertence a B.

Resposta: (255, 255, 255)

As cores comuns e seus códigos hexadecimais foram fornecidos nesta tabela.

Cor	Código Hex
Preto	# 000000
Branco	#FFFFFF
cinzento	# 808080
Vermelho	#FF0000
Green	#00FF00
Blue	#0000FF
Cyan	#00FFFF
Magenta	#FF00FF
Yellow	#FFFF00

• Average method

• Weighted method or luminosity method

Average method

Average method is the most simple one. You just have to take the average of three colors. Since its an RGB image , so it means that you have add r with g with b and then divide it by 3 to get your desired grayscale image.

Its done in this way.

Grayscale = (R + G + B) / 3

For example:

If you have an color image like the image shown above and you want to convert it into grayscale using average method. The following result would appear.

Explanation

There is one thing to be sure , that something happens to the original works. It means that our average method works. But the results were not as expected. We wanted to convert the image into a grayscale , but this turned out to be a rather black image.

Problem

This problem arise due to the fact , that we take average of the three colors. Since the three different colors have three different wavelength and have their own contribution in the formation of image , so we have to take average according to their contribution , not done it averagely using average method. Right now what we are doing is this,

33% of Red, 33% of Green, 33% of Blue

We are taking 33% of each, that means , each of the portion has same contribution in the image. But in reality thats not the case. The solution to this has been given by luminosity method.

Weighted method or luminosity method

You have seen the problem that occur in the average method. Weighted method has a solution to that problem. Since red color has more wavelength of all the three colors , and green is the color that has not only less wavelength then red color but also green is the color that gives more soothing effect to the eyes.

It means that we have to decrease the contribution of red color , and increase the contribution of the green color , and put blue color contribution in between these two.

So the new equation that form is:

New grayscale image = ( (0.3 * R) + (0.59 * G) + (0.11 * B) ).

According to this equation , Red has contribute 30% , Green has contributed 59% which is greater in all three colors and Blue has contributed 11%.

Applying this equation to the image, we get this

Original Image:

Grayscale Image:

Explanation

As you can see here , that the image has now been properly converted to grayscale using weighted method. As compare to the result of average method , this image is more brighter.

Conversion of analog signal to digital signal:

The output of most of the image sensors is an analog signal, and we can not apply digital processing on it because we can not store it. We can not store it because it requires infinite memory to store a signal that can have infinite values.

So we have to convert an analog signal into a digital signal.

To create an image which is digital , we need to covert continuous data into digital form. There are two steps in which it is done.

• Sampling

• Quantization

We will discuss sampling now , and quantization will be discussed later on but for now on we will discuss just a little about the difference between these two and the need of these two steps.

Basic idea:

The basic idea behind converting an analog signal to its digital signal is

to convert both of its axis (x,y) into a digital format.

Since an image is continuous not just in its co-ordinates (x axis) , but also in its amplitude (y axis), so the part that deals with the digitizing of co-ordinates is known as sampling. And the part that deals with digitizing the amplitude is known as quantization.

Sampling.

Sampling has already been introduced in our tutorial of introduction to signals and system. But we are going to discuss here more.

Here what we have discussed of the sampling.

The term sampling refers to take samples

We digitize x axis in sampling

It is done on independent variable

In case of equation y = sin(x), it is done on x variable

It is further divided into two parts , up sampling and down sampling

If you will look at the above figure , you will see that there are some random variations in the signal. These variations are due to noise. In sampling we reduce this noise by taking samples. It is obvious that more samples we take , the quality of the image would be more better, the noise would be more removed and same happens vice versa.

However , if you take sampling on the x axis , the signal is not converted to digital format , unless you take sampling of the y-axis too which is known as quantization. The more samples eventually means you are collecting more data, and in case of image , it means more pixels.

Relation ship with pixels

Since a pixel is a smallest element in an image. The total number of pixels in an image can be calculated as

Pixels = total no of rows * total no of columns.

Lets say we have total of 25 pixels , that means we have a square image of 5 X 5. Then as we have dicussed above in sampling , that more samples eventually result in more pixels. So it means that of our continuous signal , we have taken 25 samples on x axis. That refers to 25 pixels of this image.

This leads to another conclusion that since pixel is also the smallest division of a CCD array. So it means it has a relationship with CCD array too , which can be explained as this.

Relationship with CCD array

The number of sensors on a CCD array is directly equal to the number of pixels. And since we have concluded that the number of pixels is directly equal to the number of samples, that means that number sample is directly equal to the number of sensors on CCD array.

Oversampling.

In the beginning we have define that sampling is further categorize into two types. Which is up sampling and down sampling. Up sampling is also called as over sampling.

The oversampling has a very deep application in image processing which is known as Zooming.

Zooming

We will formally introduce zooming in the upcoming tutorial , but for now on , we will just briefly explain zooming.

Zooming refers to increase the quantity of pixels , so that when you zoom an image , you will see more detail.

The increase in the quantity of pixels is done through oversampling. The one way to zoom is , or to increase samples, is to zoom optically , through the motor movement of the lens and then capture the image. But we have to do it , once the image has been captured.

There is a difference between zooming and sampling.

The concept is same , which is, to increase samples. But the key difference is that while sampling is done on the signals , zooming is done on the digital image.

Before we define pixel resolution, it is necessary to define a pixel.

Pixel

We have already defined a pixel in our tutorial of concept of pixel, in which we define a pixel as the smallest element of an image. We also defined that a pixel can store a value proportional to the light intensity at that particular location.

Now since we have defined a pixel, we are going to define what is resolution.

Resolution

The resolution can be defined in many ways. Such as pixel resolution , spatial resolution , temporal resolution , spectral resolution. Out of which we are going to discuss pixel resolution.

You have probably seen that in your own computer settings , you have monitor resolution of 800 x 600 , 640 x 480 e.t.c

In pixel resolution , the term resolution refers to the total number of count of pixels in an digital image. For example. If an image has M rows and N columns , then its resolution can be defined as M X N.

If we define resolution as the total number of pixels , then pixel resolution can be defined with set of two numbers. The first number the width of the picture , or the pixels across columns , and the second number is height of the picture , or the pixels across its width.

We can say that the higher is the pixel resolution , the higher is the quality of the image.

We can define pixel resolution of an image as 4500 X 5500.

Megapixels

We can calculate mega pixels of a camera using pixel resolution.

Column pixels (width ) X row pixels ( height ) / 1 Million.

The size of an image can be defined by its pixel resolution.

Size = pixel resolution X bpp ( bits per pixel )

Calculating the mega pixels of the camera

Lets say we have an image of dimension: 2500 X 3192.

Its pixel resolution = 2500 * 3192 = 7982350 bytes.

Dividing it by 1 million = 7.9 = 8 mega pixel (approximately).

Aspect ratio

Another important concept with the pixel resolution is aspect ratio.

Aspect ratio is the ratio between width of an image and the height of an image. It is commonly explained as two numbers separated by a colon (8:9). This ratio differs in different images , and in different screens. The common aspect ratios are:

1.33:1, 1.37:1, 1.43:1, 1.50:1, 1.56:1, 1.66:1, 1.75:1, 1.78:1, 1.85:1, 2.00:1, e.t.c

Advantage:

Aspect ratio maintains a balance between the appearance of an image on the screen , means it maintains a ratio between horizontal and vertical pixels. It does not let the image to get distorted when aspect ratio is increased.

For example:

This is a sample image , which has 100 rows and 100 columns. If we wish to make is smaller, and the condition is that the quality remains the same or in other way the image does not get distorted , here how it happens.

Original image:

Changing the rows and columns by maintain the aspect ratio in MS Paint.

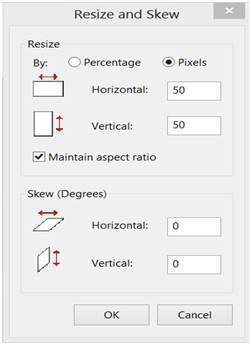
Result

Smaller image , but with same balance.

You have probably seen aspect ratios in the video players, where you can adjust the video according to your screen resolution.

Finding the dimensions of the image from aspect ratio:

Aspect ratio tells us many things. With the aspect ratio, you can calculate the dimensions of the image along with the size of the image.

For example

If you are given an image with aspect ratio of 6:2 of an image of pixel resolution of 480000 pixels given the image is an gray scale image.

And you are asked to calculate two things.

• Resolve pixel resolution to calculate the dimensions of image

• Calculate the size of the image

Solution:

Given:

Aspect ratio: c:r = 6:2

Pixel resolution: c * r = 480000

Bits per pixel: grayscale image = 8bpp

Find:

Number of rows = ?

Number of cols = ?

Solving first part:

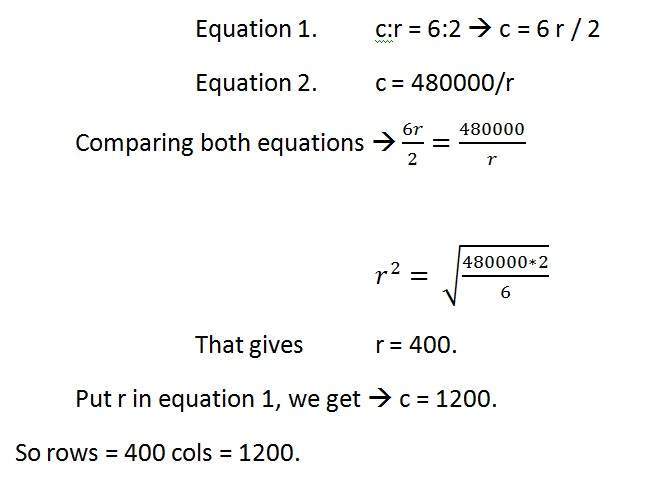
Solving 2nd part:

Size = rows * cols * bpp

Size of image in bits = 400 * 1200 * 8 = 3840000 bits

Size of image in bytes = 480000 bytes

Size of image in kilo bytes = 48 kb (approx).

In this tutorial we are going to introduce the concept of zooming , and the common techniques that are used to zoom an image.

Zooming

Zooming simply means enlarging a picture in a sense that the details in the image became more visible and clear. Zooming an image has many wide applications ranging from zooming through a camera lens , to zoom an image on internet e.t.c.

For example

is zoomed into

You can zoom something at two different steps.

The first step includes zooming before taking an particular image. This is known as pre processing zoom. This zoom involves hardware and mechanical movement.

The second step is to zoom once an image has been captured. It is done through many different algorithms in which we manipulate pixels to zoom in the required portion.

We will discuss them in detail in the next tutorial.

Optical Zoom vs digital Zoom

These two types of zoom are supported by the cameras.

Optical Zoom:

The optical zoom is achieved using the movement of the lens of your camera. An optical zoom is actually a true zoom. The result of the optical zoom is far better then that of digital zoom. In optical zoom , an image is magnified by the lens in such a way that the objects in the image appear to be closer to the camera. In optical zoom the lens is physically extend to zoom or magnify an object.

Digital Zoom:

Digital zoom is basically image processing within a camera. During a digital zoom , the center of the image is magnified and the edges of the picture got crop out. Due to magnified center , it looks like that the object is closer to you.

During a digital zoom , the pixels got expand , due to which the quality of the image is compromised.

The same effect of digital zoom can be seen after the image is taken through your computer by using an image processing toolbox / software, such as Photoshop.

The following picture is the result of digital zoom done through one of the following methods given below in the zooming methods.

Now since we are leaning digital image processing , we will not focus , on how an image can be zoomed optically using lens or other stuff. Rather we will focus on the methods, that enable to zoom a digital image.

Zooming methods:

Although there are many methods that does this job , but we are going to discuss the most common of them here.

They are listed below.

• Pixel replication or (Nearest neighbor interpolation)

• Zero order hold method

• Zooming K times

All these three methods are formally introduced in the next tutorial.

In this tutorial we are going to formally introduce three methods of zooming that were introduced in the tutorial of Introduction to zooming.

Methods

• Pixel replication or (Nearest neighbor interpolation)

• Zero order hold method

• Zooming K times

Each of the methods have their own advantages and disadvantages. We will start by discussing pixel replication.

Method 1: Pixel replication:

Introduction:

It is also known as Nearest neighbor interpolation. As its name suggest , in this method , we just replicate the neighboring pixels. As we have already discussed in the tutorial of Sampling , that zooming is nothing but increase amount of sample or pixels. This algorithm works on the same principle.

Working:

In this method we create new pixels form the already given pixels. Each pixel is replicated in this method n times row wise and column wise and you got a zoomed image. Its as simple as that.

For example:

if you have an image of 2 rows and 2 columns and you want to zoom it twice or 2 times using pixel replication, here how it can be done.

For a better understanding , the image has been taken in the form of matrix with the pixel values of the image.

1	2
3	4

The above image has two rows and two columns, we will first zoom it row wise.

Row wise zooming:

When we zoom it row wise , we will just simple copy the rows pixels to its adjacent new cell.

Here how it would be done.

1	1	2	2
3	3	4	4

As you can that in the above matrix , each pixel is replicated twice in the rows.

Column size zooming:

The next step is to replicate each of the pixel column wise, that we will simply copy the column pixel to its adjacent new column or simply below it.

Here how it would be done.

1	1	2	2
1	1	2	2
3	3	4	4
3	3	4	4

New image size:

As it can be seen from the above example , that an original image of 2 rows and 2 columns has been converted into 4 rows and 4 columns after zooming. That means the new image has a dimensions of

(Original image rows * zooming factor, Original Image cols * zooming factor)

Advantage and disadvantage:

One of the advantage of this zooming technique is , it is very simple. You just have to copy the pixels and nothing else.

The disadvantage of this technique is that image got zoomed but the output is very blurry. And as the zooming factor increased , the image got more and more blurred. That would eventually result in fully blurred image.

Method 2: Zero order hold

Introduction

Zero order hold method is another method of zooming. It is also known as zoom twice. Because it can only zoom twice. We will see in the below example that why it does that.

Working

In zero order hold method , we pick two adjacent elements from the rows respectively and then we add them and divide the result by two, and place their result in between those two elements. We first do this row wise and then we do this column wise.

For example

Lets take an image of the dimensions of 2 rows and 2 columns and zoom it twice using zero order hold.

1	2
3	4

First we will zoom it row wise and then column wise.

Row wise zooming

1	1	2
3	3	4

As we take the first two numbers : (2 + 1) = 3 and then we divide it by 2, we get 1.5 which is approximated to 1. The same method is applied in the row 2.

Column wise zooming

1	1	2
2	2	3
3	3	4

We take two adjacent column pixel values which are 1 and 3. We add them and got 4. 4 is then divided by 2 and we get 2 which is placed in between them. The same method is applied in all the columns.

New image size

As you can see that the dimensions of the new image are 3 x 3 where the original image dimensions are 2 x 2. So it means that the dimensions of the new image are based on the following formula

(2(number of rows) minus 1) X (2(number of columns) minus 1)

Advantages and disadvantage.

One of the advantage of this zooming technique , that it does not create as blurry picture as compare to the nearest neighbor interpolation method. But it also has a disadvantage that it can only run on the power of 2. It can be demonstrated here.

Reason behind twice zooming:

Consider the above image of 2 rows and 2 columns. If we have to zoom it 6 times , using zero order hold method , we can not do it. As the formula shows us this.

It could only zoom in the power of 2 2,4,8,16,32 and so on.

Even if you try to zoom it, you can not. Because at first when you will zoom it two times, and the result would be same as shown in the column wise zooming with dimensions equal to 3x3. Then you will zoom it again and you will get dimensions equal to 5 x 5. Now if you will do it again, you will get dimensions equal to 9 x 9.

Whereas according to the formula of yours the answer should be 11x11. As (6(2) minus 1) X (6(2) minus 1) gives 11 x 11.

Method 3: K-Times zooming

Introduction:

K times is the third zooming method we are going to discuss. It is one of the most perfect zooming algorithm discussed so far. It caters the challenges of both twice zooming and pixel replication. K in this zooming algorithm stands for zooming factor.

Working:

It works like this way.

First of all , you have to take two adjacent pixels as you did in the zooming twice. Then you have to subtract the smaller from the greater one. We call this output (OP).

Divide the output(OP) with the zooming factor(K). Now you have to add the result to the smaller value and put the result in between those two values.

Add the value OP again to the value you just put and place it again next to the previous putted value. You have to do it till you place k-1 values in it.

Repeat the same step for all the rows and the columns , and you get a zoomed images.

For example:

Suppose you have an image of 2 rows and 3 columns , which is given below. And you have to zoom it thrice or three times.

15	30	15
30	15	30

K in this case is 3. K = 3.

The number of values that should be inserted is k-1 = 3-1 = 2.

Row wise zooming

Take the first two adjacent pixels. Which are 15 and 30.

Subtract 15 from 30. 30-15 = 15.

Divide 15 by k. 15/k = 15/3 = 5. We call it OP.(where op is just a name)

Add OP to lower number. 15 + OP = 15 + 5 = 20.

Add OP to 20 again. 20 + OP = 20 + 5 = 25.

We do that 2 times because we have to insert k-1 values.

Now repeat this step for the next two adjacent pixels. It is shown in the first table.

After inserting the values , you have to sort the inserted values in ascending order, so there remains a symmetry between them.

It is shown in the second table

Table 1.

15	20	25	30	20	25	15
30	20	25	15	20	25	30

Table 2.

Column wise zooming

The same procedure has to be performed column wise. The procedure include taking the two adjacent pixel values, and then subtracting the smaller from the bigger one. Then after that , you have to divide it by k. Store the result as OP. Add OP to smaller one, and then again add OP to the value that comes in first addition of OP. Insert the new values.

Here what you got after all that.

15	20	25	30	25	20	15
20	21	21	25	21	21	20
25	22	22	20	22	22	25
30	25	20	15	20	25	30

New image size

The best way to calculate the formula for the dimensions of a new image is to compare the dimensions of the original image and the final image. The dimensions of the original image were 2 X 3. And the dimensions of the new image are 4 x 7.

The formula thus is:

(K (number of rows minus 1) + 1) X (K (number of cols minus 1) + 1)

Advantages and disadvantages

The one of the clear advantage that k time zooming algorithm has that it is able to compute zoom of any factor which was the power of pixel replication algorithm , also it gives improved result (less blurry) which was the power of zero order hold method. So hence It comprises the power of the two algorithms.

The only difficulty this algorithm has that it has to be sort in the end , which is an additional step , and thus increases the cost of computation.

Image resolution

Image resolution can be defined in many ways. One type of it which is pixel resolution that has been discussed in the tutorial of pixel resolution and aspect ratio.

In this tutorial, we are going to define another type of resolution which is spatial resolution.

Spatial resolution:

Spatial resolution states that the clarity of an image cannot be determined by the pixel resolution. The number of pixels in an image does not matter.

Spatial resolution can be defined as the

smallest discernible detail in an image. (Digital Image Processing - Gonzalez, Woods - 2nd Edition)

Or in other way we can define spatial resolution as the number of independent pixels values per inch.

In short what spatial resolution refers to is that we cannot compare two different types of images to see that which one is clear or which one is not. If we have to compare the two images , to see which one is more clear or which has more spatial resolution , we have to compare two images of the same size.

For example:

You cannot compare these two images to see the clarity of the image.

Although both images are of the same person , but that is not the condition we are judging on. The picture on the left is zoomed out picture of Einstein with dimensions of 227 x 222. Whereas the picture on the right side has the dimensions of 980 X 749 and also it is a zoomed image. We cannot compare them to see that which one is more clear. Remember the factor of zoom does not matter in this condition, the only thing that matters is that these two pictures are not equal.

So in order to measure spatial resolution , the pictures below would server the purpose.

Agora você pode comparar essas duas fotos. Ambas as imagens têm as mesmas dimensões que são de 227 X 222. Agora quando você as compara, você verá que a imagem do lado esquerdo tem mais resolução espacial ou é mais clara do que a imagem do lado direito. Isso ocorre porque a imagem à direita é uma imagem borrada.

Medindo a resolução espacial:

Uma vez que a resolução espacial se refere à clareza, para diferentes dispositivos, diferentes medidas foram feitas para medi-la.

Por exemplo:

• Pontos por polegada

• Linhas por polegada

• Pixels por polegada

Eles são discutidos em mais detalhes no próximo tutorial, mas apenas uma breve introdução foi fornecida abaixo.

Pontos por polegada:

Os pontos por polegada ou DPI geralmente são usados ​​em monitores.

Linhas por polegada:

Linhas por polegada ou LPI geralmente são usadas em impressoras a laser.

Pixel por polegada:

Pixel por polegada ou PPI é medido para diferentes dispositivos, como tablets, telefones celulares, etc.

No tutorial anterior de resolução espacial, discutimos a breve introdução de PPI, DPI, LPI. Agora vamos discutir formalmente todos eles.

Pixels por polegada.

A densidade de pixels ou pixels por polegada é uma medida de resolução espacial para diferentes dispositivos que incluem tablets e telefones celulares.

Quanto maior for o PPI, maior será a qualidade. Para entender melhor, é assim que calcula. Vamos calcular o PPI de um telefone móvel.

Calculando pixels por polegada (PPI) do Samsung galaxy S4:

O Samsung galaxy s4 tem PPI ou densidade de pixel de 441. Mas como ele é calculado?

Em primeiro lugar, vamos teorema de Pitágoras para calcular a resolução diagonal em pixels.

Pode ser dado como:

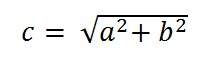
Onde aeb são as resoluções de altura e largura em pixels e c é a resolução diagonal em pixels.

Para Samsung galaxy s4, é 1080 x 1920 pixels.

Então, colocar esses valores na equação dá o resultado

C = 2202,90717

Agora vamos calcular PPI

PPI = c / tamanho diagonal em polegadas

O tamanho da diagonal em polegadas do Samsun galaxy s4 é de 5,0 polegadas, o que pode ser confirmado de qualquer lugar.

PPI = 2202.90717 / 5.0

PPI = 440,58

PPI = 441 (aprox)

Isso significa que a densidade de pixels do Samsung galaxy s4 é 441 PPI.

Pontos por polegada.

O dpi geralmente está relacionado ao PPI, embora haja uma diferença entre os dois. DPI ou pontos por polegada é uma medida da resolução espacial das impressoras. No caso de impressoras, dpi significa quantos pontos de tinta são impressos por polegada quando uma imagem é impressa na impressora.

Lembre-se de que não é necessário que cada Pixel por polegada seja impresso por um ponto por polegada. Pode haver muitos pontos por polegada usados ​​para imprimir um pixel. A razão por trás disso é que a maioria das impressoras coloridas usa o modelo CMYK. As cores são limitadas. A impressora tem que escolher entre essas cores para fazer a cor do pixel, enquanto no PC você tem centenas de milhares de cores.

Quanto maior for o dpi da impressora, maior será a qualidade do documento impresso ou imagem no papel.

Normalmente, algumas das impressoras a laser têm dpi de 300 e algumas têm 600 ou mais.

Linhas por polegada.

Quando dpi se refere a pontos por polegada, forro por polegada se refere a linhas de pontos por polegada. A resolução da tela de meio-tom é medida em linhas por polegada.

A tabela a seguir mostra algumas das linhas por polegada da capacidade das impressoras.

Impressora	LPI
Impressão de tela	45-65 lpi
Impressora laser (300 dpi)	65 lpi
Impressora laser (600 dpi)	85-105 lpi
Offset Press (papel jornal)	85 lpi
Offset Press (papel revestido)	85-185 lpi

Resolução de imagem:

Resolução de nível de cinza:

A resolução do nível de cinza refere-se à mudança previsível ou determinística nos tons ou níveis de cinza em uma imagem.

Resumindo, a resolução do nível de cinza é igual ao número de bits por pixel.

Já discutimos bits por pixel em nosso tutorial de bits por pixel e requisitos de armazenamento de imagem. Vamos definir o bpp aqui brevemente.

BPP:

O número de cores diferentes em uma imagem depende da profundidade da cor ou bits por pixel.

Matematicamente:

A relação matemática que pode ser estabelecida entre a resolução do nível de cinza e bits por pixel pode ser dada como.

Nesta equação, L se refere ao número de níveis de cinza. Também pode ser definido como tons de cinza. E k refere-se a bpp ou bits por pixel. Portanto, o aumento de 2 à potência de bits por pixel é igual à resolução do nível de cinza.

Por exemplo:

A imagem acima de Einstein é uma imagem em escala de cinza. Significa que é uma imagem com 8 bits por pixel ou 8bpp.

Agora, se fosse calcular a resolução do nível de cinza, aqui está como o faremos.

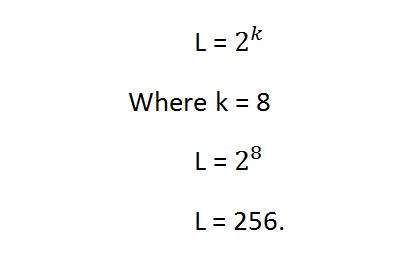
Isso significa que a resolução do nível de cinza é 256. Ou de outra forma, podemos dizer que esta imagem tem 256 tons diferentes de cinza.

Quanto maior for o número de bits por pixel de uma imagem, maior será a resolução do seu nível de cinza.

Definindo a resolução do nível de cinza em termos de bpp:

Não é necessário que uma resolução de nível de cinza seja definida apenas em termos de níveis. Também podemos defini-lo em termos de bits por pixel.

Por exemplo:

Se você receber uma imagem de 4 bpp e for solicitado a calcular sua resolução de nível de cinza. Existem duas respostas para essa pergunta.

A primeira resposta é 16 níveis.

A segunda resposta é de 4 bits.

Encontrar bpp a partir da resolução de nível de cinza:

Você também pode encontrar os bits por pixels da resolução de nível de cinza fornecida. Para isso, basta torcer um pouco a fórmula.

Equação 1.

Esta fórmula encontra os níveis. Agora, se formos encontrar os bits por pixel ou, neste caso, k, vamos simplesmente alterá-lo assim.

K = log base 2 (L) Equação (2)

Porque na primeira equação a relação entre Níveis (L) e bits por pixel (k) é exponencial. Agora temos que revertê-lo e, portanto, o inverso do exponencial é log.

Vamos dar um exemplo para encontrar bits por pixel da resolução de nível de cinza.

Por exemplo:

Se você receber uma imagem de 256 níveis. Quais são os bits por pixel necessários para isso.

Colocando 256 na equação, obtemos.

K = log de base 2 (256)

K = 8.

Portanto, a resposta é 8 bits por pixel.

Resolução e quantização do nível de cinza:

A quantização será introduzida formalmente no próximo tutorial, mas aqui vamos apenas explicar a relação entre a resolução do nível de cinza e a quantização.

A resolução do nível de cinza é encontrada no eixo y do sinal. No tutorial de Introdução aos sinais e sistema, estudamos que a digitalização de um sinal analógico requer duas etapas. Amostragem e quantização.

A amostragem é feita no eixo x. E a quantização é feita no eixo Y.

Isso significa que a digitalização da resolução do nível de cinza de uma imagem é feita na quantização.

Introduzimos a quantização em nosso tutorial de sinais e sistema. Iremos relacioná-lo formalmente com imagens digitais neste tutorial. Vamos discutir primeiro um pouco sobre a quantização.

Digitalizando um sinal.

Como vimos nos tutoriais anteriores, a digitalização de um sinal analógico em um digital requer duas etapas básicas. Amostragem e quantização. A amostragem é feita no eixo x. É a conversão do eixo x (valores infinitos) em valores digitais.

A figura abaixo mostra a amostragem de um sinal.

Amostragem em relação às imagens digitais:

O conceito de amostragem está diretamente relacionado ao zoom. Quanto mais amostras você tira, mais pixels você obtém. A sobreamostragem também pode ser chamada de zoom. Isso foi discutido no tutorial de amostragem e zoom.

Mas a história da digitalização de um sinal não termina na amostragem também, há outra etapa envolvida que é conhecida como Quantização.

O que é quantização.

A quantização é oposta à amostragem. Isso é feito no eixo y. Quando você está qunaitizing uma imagem, na verdade você está dividindo um sinal em quanta (partições).

No eixo x do sinal, estão os valores das coordenadas, e no eixo y, temos as amplitudes. Portanto, digitalizar as amplitudes é conhecido como Quantização.

Aqui como é feito

Você pode ver nesta imagem, que o sinal foi quantificado em três níveis diferentes. Isso significa que quando amostramos uma imagem, na verdade reunimos muitos valores e, na quantização, definimos níveis para esses valores. Isso pode ficar mais claro na imagem abaixo.

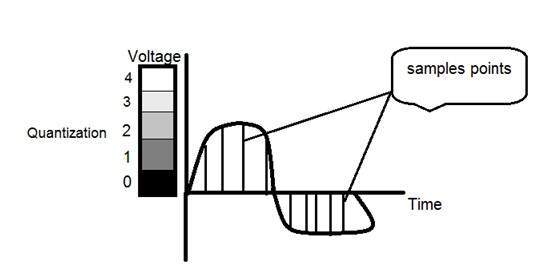
Na figura mostrada na amostragem, embora as amostras tenham sido tomadas, elas ainda estavam se estendendo verticalmente para uma faixa contínua de valores de nível de cinza. Na figura mostrada acima, esses valores de variação vertical foram quantizados em 5 níveis ou partições diferentes. Variando de 0 preto a 4 branco. Este nível pode variar de acordo com o tipo de imagem desejada.

A relação da quantização com os níveis de cinza foi discutida mais detalhadamente abaixo.

Relação de quantização com resolução de nível de cinza:

A figura quantizada mostrada acima possui 5 níveis diferentes de cinza. Isso significa que a imagem formada a partir desse sinal, teria apenas 5 cores diferentes. Seria uma imagem em preto e branco mais ou menos com algumas cores de cinza. Agora, se você quiser melhorar a qualidade da imagem, há uma coisa que você pode fazer aqui. Ou seja, para aumentar os níveis, ou aumentar a resolução do nível de cinza. Se você aumentar este nível para 256, significa que tem uma imagem em escala de cinza. O que é muito melhor do que a imagem em preto e branco simples.

Agora 256, ou 5 ou qualquer nível que você escolher é chamado de nível de cinza. Lembre-se da fórmula que discutimos no tutorial anterior de resolução de nível de cinza que é,

Discutimos que o nível de cinza pode ser definido de duas maneiras. Quais eram esses dois.

• Nível de cinza = número de bits por pixel (BPP). (K na equação)

• Nível de cinza = número de níveis por pixel.

Neste caso, temos o nível de cinza igual a 256. Se tivermos que calcular o número de bits, simplesmente colocaremos os valores na equação. No caso de 256 níveis, temos 256 tons diferentes de cinza e 8 bits por pixel, portanto, a imagem seria uma imagem em escala de cinza.

Reduzindo o nível de cinza

Agora vamos reduzir os níveis de cinza da imagem para ver o efeito na imagem.

Por exemplo:

Digamos que você tenha uma imagem de 8bpp, que tem 256 níveis diferentes. É uma imagem em tons de cinza e a imagem parece algo assim.

256 níveis de cinza

Agora vamos começar a reduzir os níveis de cinza. Primeiro, reduziremos os níveis de cinza de 256 para 128.

128 níveis de cinza

Não há muito efeito em uma imagem após diminuir os níveis de cinza para a metade. Vamos diminuir um pouco mais.

64 níveis de cinza

Ainda sem muito efeito, vamos reduzir mais os níveis.

32 níveis de cinza

Surpreso ao ver que ainda há um pouco de efeito. Pode ser por uma razão, que seja a foto do Einstein, mas vamos reduzir mais os níveis.

16 níveis de cinza

Boom aqui, vamos, a imagem finalmente revela, que é afetado pelos níveis.

8 níveis de cinza

4 níveis de cinza

Agora, antes de reduzi-lo, mais dois 2 níveis, você pode facilmente ver que a imagem foi muito distorcida ao reduzir os níveis de cinza. Agora vamos reduzi-lo para 2 níveis, o que nada mais é do que um simples nível de preto e branco. Isso significa que a imagem seria uma imagem simples em preto e branco.

2 níveis de cinza

Esse é o último nível que podemos alcançar, pois se reduzíssemos ainda mais, seria simplesmente uma imagem em preto, que não pode ser interpretada.

Contornando:

Há uma observação interessante aqui, que à medida que reduzimos o número de níveis de cinza, há um tipo especial de efeito que começa a aparecer na imagem, que pode ser visto claramente em uma imagem de 16 níveis de cinza. Este efeito é conhecido como Contorno.

Curvas de preferência Iso:

A resposta para esse efeito, e por isso que aparece, está nas curvas de preferência Iso. Eles são discutidos em nosso próximo tutorial de curvas de preferência de contorno e Iso.

O que é contorno?

À medida que diminuímos o número de níveis de cinza em uma imagem, algumas cores falsas ou bordas começam a aparecer em uma imagem. Isso foi mostrado em nosso último tutorial de Quantização.

Vamos dar uma olhada nisso.

Considere que temos uma imagem de 8bpp (uma imagem em tons de cinza) com 256 tons diferentes de cinza ou níveis de cinza.

A imagem acima tem 256 tons diferentes de cinza. Agora, quando reduzimos para 128 e reduzimos ainda mais para 64, a imagem é mais ou menos a mesma. Mas ao reduzir ainda mais para 32 níveis diferentes, temos uma imagem como esta

Se você olhar de perto, verá que os efeitos começam a aparecer na imagem. Esses efeitos são mais visíveis quando os reduzimos ainda mais para 16 níveis e obtivemos uma imagem como esta.

Essas linhas, que começam a aparecer nesta imagem são conhecidas como contornos, que são bem visíveis na imagem acima.

Aumento e diminuição do contorno

O efeito do contorno aumenta à medida que reduzimos o número de níveis de cinza e o efeito diminui à medida que aumentamos o número de níveis de cinza. Ambos são vice-versa

VS

Isso significa mais quantização, terá efeito em mais contorno e vice-versa. Mas é sempre assim. A resposta é Não. Isso depende de outra coisa que será discutida abaixo.

Curvas de isopreferência

Um estudo realizado sobre este efeito de nível de cinza e contorno, e os resultados foram apresentados no gráfico na forma de curvas, conhecidas como curvas de preferência Iso.

O fenômeno das curvas Isopreference mostra que o efeito do contorno não depende apenas da diminuição da resolução do nível de cinza, mas também do detalhe da imagem.

A essência do estudo é:

Se uma imagem tiver mais detalhes, o efeito de contorno passaria a aparecer nesta imagem posteriormente, ao comparar com uma imagem que tem menos detalhes, quando os níveis de cinza são quantizados.

De acordo com a pesquisa original, os pesquisadores pegaram essas três imagens e variaram a resolução do nível de cinza, nas três imagens.

As imagens eram

Nível de detalhe:

A primeira imagem tem apenas um rosto e, portanto, muito menos detalhes. A segunda imagem também possui alguns outros objetos na imagem, como o camera man, sua câmera, suporte da câmera e objetos de fundo, etc. Considerando que a terceira imagem tem mais detalhes do que todas as outras imagens.

Experimentar:

A resolução do nível de cinza foi variada em todas as imagens, e o público foi solicitado a avaliar essas três imagens subjetivamente. Após a classificação, foi traçado um gráfico de acordo com os resultados.

Resultado:

O resultado foi desenhado no gráfico. Cada curva do gráfico representa uma imagem. Os valores no eixo x representam o número de níveis de cinza e os valores no eixo y representam bits por pixel (k).

O gráfico é mostrado abaixo.

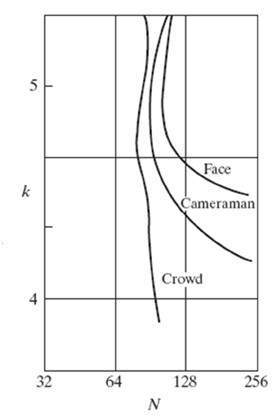
De acordo com este gráfico, podemos ver que a primeira imagem que era de rosto, foi sujeita a contornos logo no início que todas as outras duas imagens. A segunda imagem, que era do cameraman, foi sujeita a contornos um pouco depois da primeira imagem quando seus níveis de cinza são reduzidos. Isso porque ela tem mais detalhes do que a primeira imagem. E a terceira imagem ficou bastante contornada após as duas primeiras imagens ou seja: após 4 bpp. Isso porque, essa imagem tem mais detalhes.

Conclusão:

Portanto, para imagens mais detalhadas, as curvas de isopreferência tornam-se cada vez mais verticais. Isso também significa que, para uma imagem com muitos detalhes, são necessários poucos níveis de cinza.

Nos últimos dois tutoriais de quantização e contorno, vimos que reduzir o nível de cinza de uma imagem reduz o número de cores necessárias para denotar uma imagem. Se os níveis de cinza forem reduzidos em dois 2, a imagem que aparece não tem muita resolução espacial ou não é muito atraente.

Dithering:

Dithering é o processo pelo qual criamos ilusões da cor que não estão realmente presentes. Isso é feito pelo arranjo aleatório de pixels.

Por exemplo. Considere esta imagem.

Esta é uma imagem com apenas pixels em preto e branco. Seus pixels são organizados em uma ordem para formar outra imagem que é mostrada abaixo. Observe que a disposição dos pixels foi alterada, mas não a quantidade de pixels.

Por que hesitar?

Por que precisamos hesitar, a resposta está em sua relação com a quantização.

Dithering com quantização.

Quando realizamos a quantização, até o último nível, vemos que a imagem que vem no último nível (nível 2) é assim.

Agora, como podemos ver pela imagem aqui, a imagem não é muito clara, especialmente se você olhar para o braço esquerdo e atrás da imagem do Einstein. Também esta foto não contém muitas informações ou detalhes do Einstein.

Agora, se formos mudar esta imagem para alguma imagem que forneça mais detalhes do que isso, temos que executar o pontilhamento.

Executando dithering.

Em primeiro lugar, vamos trabalhar na trégua. O pontilhamento geralmente funciona para melhorar o limiar. Durante a retenção, as bordas nítidas aparecem onde os gradientes são suaves em uma imagem.

Na limiarização, simplesmente escolhemos um valor constante. Todos os pixels acima desse valor são considerados 1 e todos os valores abaixo dele são considerados 0.

Conseguimos essa imagem após o limite.

Pois não há muita mudança na imagem, pois os valores já são 0 e 1 ou preto e branco nesta imagem.

Agora nós executamos algum dithering aleatório nele. É algum arranjo aleatório de pixels.

Conseguimos uma imagem que dá mais detalhes, mas seu contraste é muito baixo.

Então, fazemos mais pontilhamento que aumentará o contraste. A imagem que obtivemos é esta:

Agora nós misturamos os conceitos de dithering aleatório, junto com o threshold e temos uma imagem como esta.

Agora você vê, nós temos todas essas imagens apenas reorganizando os pixels de uma imagem. Esse rearranjo pode ser aleatório ou de acordo com alguma medida.

Antes de discutir o uso de histogramas no processamento de imagens, veremos primeiro o que é histograma, como ele é usado e, a seguir, um exemplo de histogramas para entender melhor o histograma.

Histogramas:

Um histograma é um gráfico. Um gráfico que mostra a frequência de qualquer coisa. Normalmente, o histograma tem barras que representam a frequência de ocorrência de dados em todo o conjunto de dados.

Um histograma possui dois eixos, o eixo xeo eixo y.

O eixo x contém eventos cuja frequência você deve contar.

O eixo y contém a frequência.

As diferentes alturas de barra mostram diferentes frequências de ocorrência de dados.

Normalmente, um histograma se parece com isso.

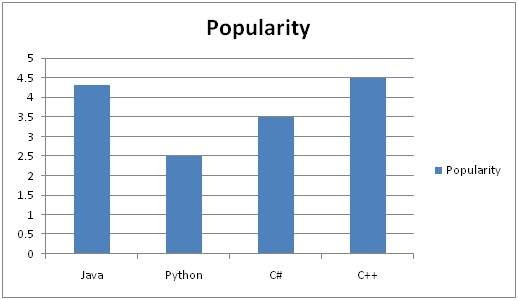
Agora veremos um exemplo deste histograma é construir

Exemplo:

Considere uma classe de alunos de programação e você estará ensinando Python para eles.

No final do semestre, você obteve esse resultado que está mostrado na tabela. Mas é muito confuso e não mostra o resultado geral da aula. Então você tem que fazer um histograma do seu resultado, mostrando a frequência geral de ocorrência das notas em sua classe. Veja como você vai fazer.

Folha de resultados:

Nome	Grau
John	UMA
Jack	D
Carter	B
Tommy	UMA
Lisa	C +
Derek	UMA-
Tom	B +

Histograma da folha de resultados:

Agora o que você vai fazer é descobrir o que vem nos eixos xey.

Há uma coisa a ter certeza: o eixo y contém a frequência, então o que vem no eixo x. O eixo X contém o evento cuja frequência deve ser calculada. Neste caso, o eixo x contém graus.

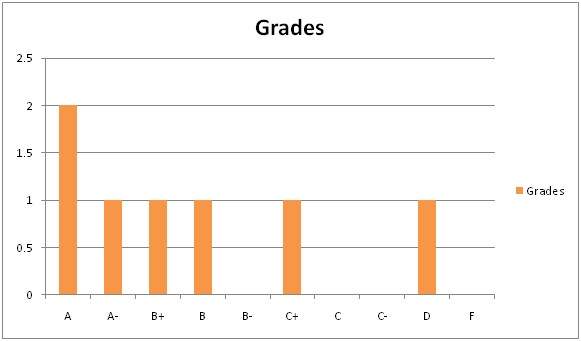
Agora veremos como usamos um histograma em uma imagem.

Histograma de uma imagem

O histograma de uma imagem, como outros histogramas, também mostra a frequência. Mas um histograma de imagem mostra a frequência dos valores de intensidade dos pixels. Em um histograma de imagem, o eixo x mostra as intensidades dos níveis de cinza e o eixo y mostra a frequência dessas intensidades.

Por exemplo:

O histograma da imagem acima do Einstein seria algo assim

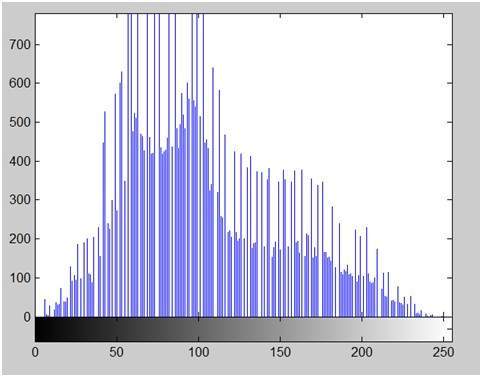
O eixo x do histograma mostra a faixa de valores de pixel. Como é uma imagem de 8 bpp, isso significa que tem 256 níveis de cinza ou tons de cinza. É por isso que o intervalo do eixo x começa em 0 e termina em 255 com um intervalo de 50. Enquanto no eixo y, está a contagem dessas intensidades.

Como você pode ver no gráfico, a maioria das barras que têm alta frequência fica na primeira metade, que é a parte mais escura. Isso significa que a imagem que obtivemos é mais escura. E isso também pode ser comprovado pela imagem.

Aplicações de histogramas:

Os histogramas têm muitos usos no processamento de imagens. O primeiro uso, como também foi discutido acima, é a análise da imagem. Podemos predizer sobre uma imagem apenas olhando seu histograma. É como olhar um raio-x de um osso de um corpo.

O segundo uso do histograma é para fins de brilho. Os histogramas têm ampla aplicação no brilho da imagem. Não apenas no brilho, mas os histogramas também são usados ​​para ajustar o contraste de uma imagem.

Outro uso importante do histograma é para equalizar uma imagem.

E por último, mas não menos importante, o histograma tem amplo uso em limiares. Isso é usado principalmente em visão computacional.

Brilho:

Brilho é um termo relativo. Depende da sua percepção visual. Como o brilho é um termo relativo, o brilho pode ser definido como a quantidade de energia produzida por uma fonte de luz em relação à fonte com a qual estamos comparando. Em alguns casos, podemos facilmente dizer que a imagem é brilhante e, em alguns casos, não é fácil de perceber.

Por exemplo:

Basta dar uma olhada em ambas as imagens e comparar qual delas é mais brilhante.

Podemos ver facilmente que a imagem do lado direito é mais brilhante do que a imagem da esquerda.

Mas se a imagem à direita ficar mais escura que a primeira, então podemos dizer que a imagem à esquerda é mais clara que a esquerda.

Como tornar uma imagem mais brilhante.

O brilho pode ser simplesmente aumentado ou diminuído por simples adição ou subtração à matriz da imagem.

Considere esta imagem preta de 5 linhas e 5 colunas

Como já sabemos, que cada imagem tem uma matriz atrás que contém os valores dos pixels. Esta matriz de imagem é fornecida abaixo.

0	0	0	0	0
0	0	0	0	0
0	0	0	0	0
0	0	0	0	0
0	0	0	0	0

Uma vez que toda a matriz é preenchida com zero, e a imagem é muito mais escura.

Agora vamos compará-la com outra mesma imagem preta para ver se esta imagem ficou mais brilhante ou não.

Mesmo assim as duas imagens são iguais, agora vamos realizar algumas operações na imagem1, devido a que ela se torna mais brilhante que a segunda.

O que faremos é simplesmente adicionar um valor de 1 a cada um dos valores da matriz da imagem 1. Depois de adicionar a imagem, 1 faria algo assim.

Agora iremos compará-lo novamente com a imagem 2 e ver qualquer diferença.

Vemos que ainda não podemos dizer qual imagem é mais brilhante, pois ambas as imagens parecem iguais.

Agora o que faremos, adicionaremos 50 a cada um dos valores de matriz da imagem 1 e veremos em que a imagem se tornou.

A saída é fornecida abaixo.

Agora, novamente, vamos compará-lo com a imagem 2.

Agora você pode ver que a imagem 1 é um pouco mais clara que a imagem 2. Seguimos e adicionamos outro valor 45 à sua matriz da imagem 1, e desta vez comparamos novamente as duas imagens.

Agora, ao comparar, você pode ver que esta imagem1 é claramente mais brilhante que a imagem 2.

Mesmo é mais brilhante do que a imagem antiga1. Neste ponto, a matriz da imagem1 contém 100 em cada índice, primeiro adicione 5, depois 50 e depois 45. Portanto, 5 + 50 + 45 = 100.

Contraste

O contraste pode ser explicado simplesmente como a diferença entre a intensidade máxima e mínima do pixel em uma imagem.

Por exemplo.

Considere a imagem final1 em brilho.

A matriz desta imagem é:

100	100	100	100	100
100	100	100	100	100
100	100	100	100	100
100	100	100	100	100
100	100	100	100	100

O valor máximo nesta matriz é 100.

O valor mínimo nesta matriz é 100.

Contraste = intensidade máxima do pixel (subtraída por) intensidade mínima do pixel

= 100 (subtraído por) 100

= 0

0 significa que esta imagem tem contraste 0.

Antes de discutirmos o que é transformação de imagem, discutiremos o que é transformação.

Transformação.

A transformação é uma função. Uma função que mapeia um conjunto para outro após realizar algumas operações.

Sistema de processamento digital de imagens:

Já vimos nos tutoriais introdutórios que no processamento digital de imagens, desenvolveremos um sistema cuja entrada seria uma imagem e a saída também seria uma imagem. E o sistema realizaria algum processamento na imagem de entrada e forneceria sua saída como uma imagem processada. É mostrado abaixo.

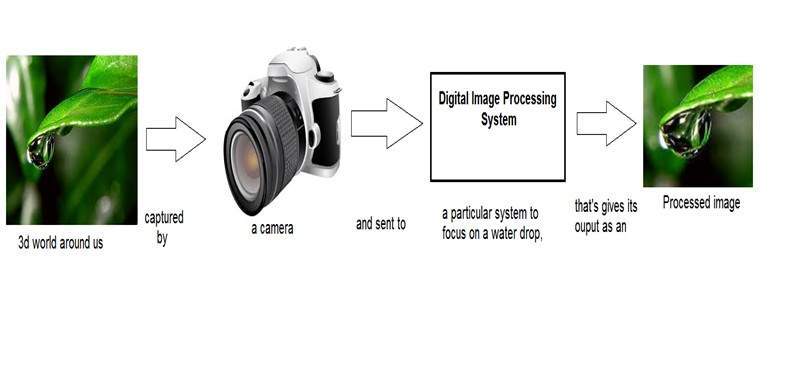
Agora a função aplicada dentro deste sistema digital que processa uma imagem e a converte em saída pode ser chamada de função de transformação.

Como mostra a transformação ou relação, é assim que uma imagem1 é convertida em imagem2.

Transformação de imagem.

Considere esta equação

G (x, y) = T {f (x, y)}

Nesta equação,

F (x, y) = imagem de entrada na qual a função de transformação deve ser aplicada.

G (x, y) = a imagem de saída ou imagem processada.

T é a função de transformação.

Essa relação entre a imagem de entrada e a imagem de saída processada também pode ser representada como.

s = T (r)

onde r é realmente o valor do pixel ou intensidade do nível de cinza de f (x, y) em qualquer ponto. E s é o valor do pixel ou intensidade do nível de cinza de g (x, y) em qualquer ponto.

A transformação básica de nível de cinza foi discutida em nosso tutorial de transformações básicas de nível de cinza.

Agora vamos discutir algumas das funções básicas de transformação.

Exemplos:

Considere esta função de transformação.

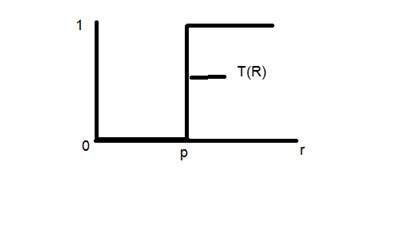
Vamos considerar o ponto r como 256 e o ​​ponto p como 127. Considere esta imagem como uma imagem de um bpp. Isso significa que temos apenas dois níveis de intensidades que são 0 e 1. Portanto, neste caso, a transformação mostrada pelo gráfico pode ser explicada como.

Todos os valores de intensidade de pixel que estão abaixo de 127 (ponto p) são 0, significa preto. E todos os valores de intensidade de pixel maiores que 127 são 1, o que significa branco. Mas, no ponto exato de 127, há uma mudança repentina na transmissão, então não podemos dizer que, naquele ponto exato, o valor seria 0 ou 1.

Matematicamente, essa função de transformação pode ser denotada como:

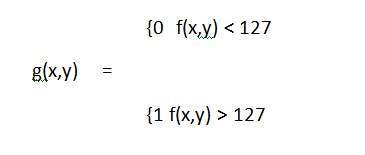
Considere outra transformação como esta:

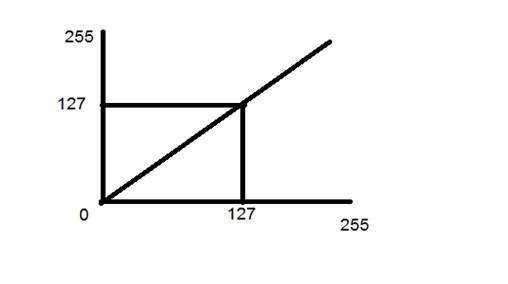
Agora, se você olhar este gráfico em particular, verá uma linha de transição reta entre a imagem de entrada e a imagem de saída.

Mostra que para cada pixel ou valor de intensidade da imagem de entrada, existe um mesmo valor de intensidade da imagem de saída. Isso significa que a imagem de saída é uma réplica exata da imagem de entrada.

Pode ser representado matematicamente como:

g (x, y) = f (x, y)

a imagem de entrada e saída seriam neste caso são mostradas abaixo.

O conceito básico de histogramas foi discutido no tutorial de Introdução aos histogramas. Mas vamos apresentar brevemente o histograma aqui.

Histograma:

O histograma nada mais é do que um gráfico que mostra a frequência de ocorrência dos dados. Os histogramas têm muitas utilidades no processamento de imagens, das quais iremos discutir um usuário aqui, que é chamado de deslizamento de histograma.

Deslizamento do histograma.

No deslizamento do histograma, simplesmente deslocamos um histograma completo para a direita ou para a esquerda. Devido ao deslocamento ou deslizamento do histograma para a direita ou esquerda, uma mudança clara pode ser vista na imagem. Neste tutorial, usaremos o deslizamento do histograma para manipular o brilho.

O termo isto é: Brilho foi discutido em nosso tutorial de introdução ao brilho e contraste. Mas vamos definir brevemente aqui.

Brilho:

Brilho é um termo relativo. O brilho pode ser definido como a intensidade da luz emitida por uma fonte de luz específica.

Contraste:

O contraste pode ser definido como a diferença entre a intensidade máxima e mínima do pixel em uma imagem.

Histogramas deslizantes

Aumentar o brilho usando deslizamento do histograma

O histograma desta imagem é mostrado abaixo.

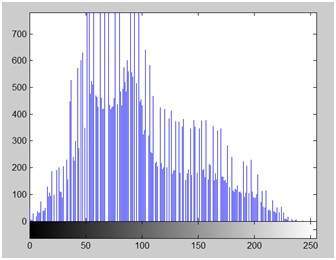
No eixo y deste histograma estão a frequência ou contagem. E no eixo x, temos valores de nível de cinza. Como você pode ver no histograma acima, as intensidades dos níveis de cinza, cuja contagem é superior a 700, estão na primeira metade, significam para a parte mais escura. É por isso que obtivemos uma imagem um pouco mais escura.

Para iluminá-lo, vamos deslizar seu histograma para a direita ou para a parte mais branca. Para fazer isso, precisamos adicionar pelo menos um valor de 50 a esta imagem. Porque podemos ver pelo histograma acima, que esta imagem também tem intensidade de 0 pixel, que é preto puro. Portanto, se adicionarmos 0 a 50, mudaremos todos os valores da intensidade 0 para a intensidade 50 e todos os demais valores serão alterados de acordo.

Vamos fazer isso.

Aqui está o que obtivemos após adicionar 50 a cada intensidade de pixel.

A imagem foi mostrada abaixo.

E seu histograma foi mostrado abaixo.

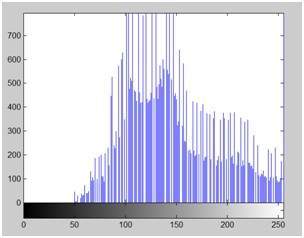
Vamos comparar essas duas imagens e seus histogramas para ver quais mudanças devem ocorrer.

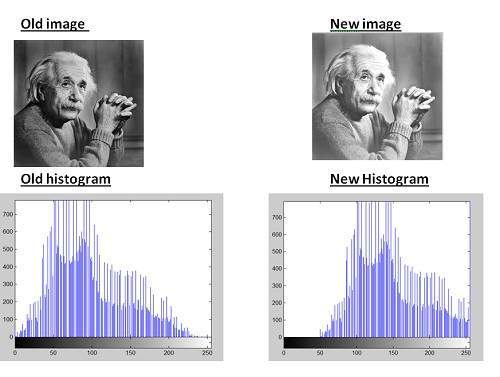
Conclusão:

Como podemos ver claramente no novo histograma, todos os valores dos pixels foram deslocados para a direita e seu efeito pode ser visto na nova imagem.

Diminuindo o brilho usando deslizamento do histograma

Agora, se tivéssemos que diminuir o brilho dessa nova imagem a tal ponto que a imagem antiga parecesse mais brilhante, teríamos que subtrair algum valor de toda a matriz da nova imagem. O valor que vamos subtrair é 80. Como já adicionamos 50 à imagem original e temos uma nova imagem mais clara, agora se quisermos torná-la mais escura, temos que subtrair pelo menos mais de 50 dela.

E foi isso que obtivemos depois de subtrair 80 da nova imagem.

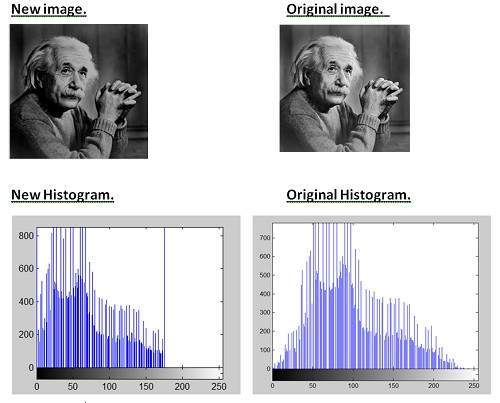
Conclusão:

É claro a partir do histograma da nova imagem, que todos os valores de pixel foram deslocados para a direita e, portanto, pode ser validado a partir da imagem que a nova imagem está mais escura e agora a imagem original parece mais brilhante em comparação com esta nova imagem.

Uma das outras vantagens dos histogramas que discutimos em nosso tutorial de introdução aos histogramas é o aprimoramento do contraste.

Existem dois métodos para aumentar o contraste. O primeiro é chamado de alongamento de histograma que aumenta o contraste. O segundo é chamado de equalização de histograma que aumenta o contraste e foi discutido em nosso tutorial de equalização de histograma.

Antes de discutirmos o alongamento do histograma para aumentar o contraste, definiremos brevemente o contraste.

Contraste.

O contraste é a diferença entre a intensidade máxima e mínima do pixel.

Considere esta imagem.

O histograma desta imagem é mostrado abaixo.

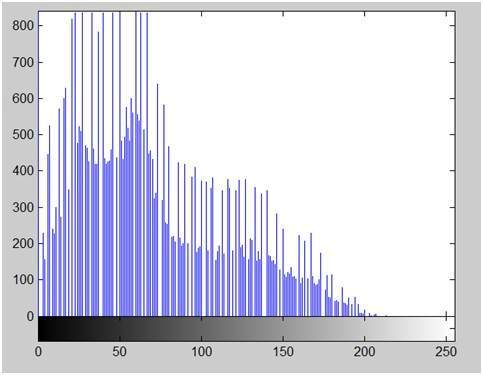
Agora calculamos o contraste a partir desta imagem.

Contraste = 225.

Agora vamos aumentar o contraste da imagem.

Aumentando o contraste da imagem:

A fórmula para esticar o histograma da imagem para aumentar o contraste é

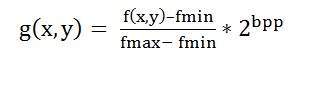
A fórmula requer encontrar a intensidade de pixel mínima e máxima multiplicada por níveis de cinza. Em nosso caso, a imagem tem 8bpp, então os níveis de cinza são 256.

O valor mínimo é 0 e o valor máximo é 225. Portanto, a fórmula em nosso caso é

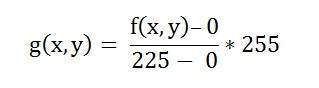
onde f (x, y) denota o valor de cada intensidade de pixel. Para cada f (x, y) em uma imagem, calcularemos esta fórmula.

Depois de fazer isso, seremos capazes de aumentar nosso contraste.

A imagem a seguir aparece após aplicar o alongamento do histograma.

O histograma ampliado desta imagem é mostrado abaixo.

Observe a forma e a simetria do histograma. O histograma agora está alongado ou, de outra forma, expandido. Dê uma olhada nisso.

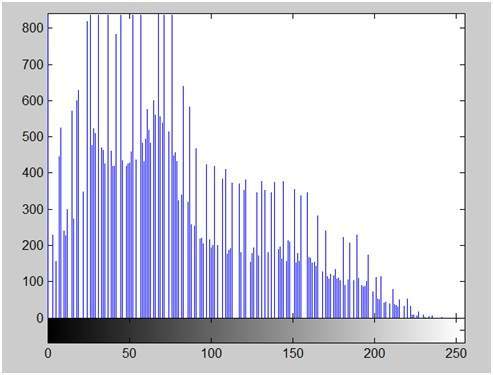
Neste caso, o contraste da imagem pode ser calculado como

Contraste = 240

Portanto, podemos dizer que o contraste da imagem é aumentado.

Nota: este método de aumentar o contraste nem sempre funciona, mas falha em alguns casos.

Falha de alongamento do histograma

Como já discutimos, o algoritmo falha em alguns casos. Esses casos incluem imagens com quando há intensidade de pixel 0 e 255 estão presentes na imagem

Porque quando as intensidades de pixel 0 e 255 estão presentes em uma imagem, então nesse caso elas se tornam a intensidade mínima e máxima do pixel, o que estraga a fórmula como esta.

Fórmula Original

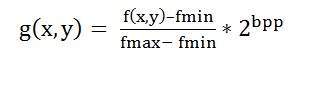
Colocando valores de caso de falha na fórmula:

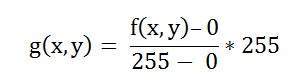
Simplifique que a expressão dá

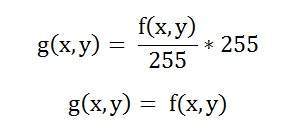
Isso significa que a imagem de saída é igual à imagem processada. Isso significa que não há efeito de alongamento do histograma feito nesta imagem.

Ambos os termos PMF e CDF pertencem à probabilidade e à estatística. Agora, a questão que deve surgir em sua mente é por que estamos estudando probabilidade. É porque esses dois conceitos de PMF e CDF serão usados ​​no próximo tutorial de equalização de histograma. Então, se você não sabe como calcular PMF e CDF, você não pode aplicar equalização de histograma em sua imagem

What is PMF?

PMF stands for probability mass function. As it name suggest , it gives the probability of each number in the data set or you can say that it basically gives the count or frequency of each element.

How PMF is calculated:

We will calculate PMF from two different ways. First from a matrix , because in the next tutorial , we have to calculate the PMF from a matrix , and an image is nothing more then a two dimensional matrix.

Then we will take another example in which we will calculate PMF from the histogram.

Consider this matrix.

1	2	7	5	6
7	2	3	4	5
0	1	5	7	3
1	2	5	6	7
6	1	0	3	4

Now if we were to calculate the PMF of this matrix , here how we are going to do it.

At first , we will take the first value in the matrix , and then we will count , how much time this value appears in the whole matrix. After count they can either be represented in a histogram , or in a table like this below.

PMF

0	2	2/25
1	4	4/25
2	3	3/25
3	3	3/25
4	2	2/25
5	4	4/25
6	3	3/25
7	4	4/25

Note that the sum of the count must be equal to total number of values.

Calculating PMF from histogram

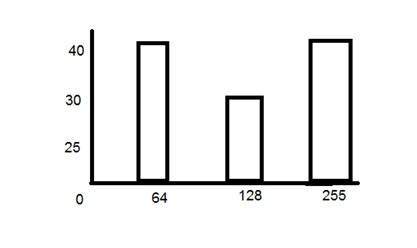
The above histogram shows frequency of gray level values for an 8 bits per pixel image.

Now if we have to calculate its PMF , we will simple look at the count of each bar from vertical axis and then divide it by total count.

So the PMF of the above histogram is this.

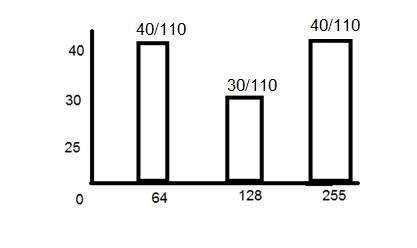
Another important thing to note in the above histogram is that it is not monotonically increasing. So in order to increase it monotonically, we will calculate its CDF.

What is CDF?

CDF stands for cumulative distributive function. It is a function that calculates the cumulative sum of all the values that are calculated by PMF. It basically sums the previous one.

How it is calculated?

We will calculate CDF using a histogram. Here how it is done. Consider the histogram shown above which shows PMF.

Since this histogram is not increasing monotonically , so will make it grow monotonically.

We will simply keep the first value as it is , and then in the 2nd value , we will add the first one and so on.

Here is the CDF of the above PMF function.

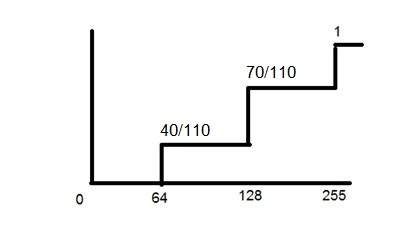
Now as you can see from the graph above , that the first value of PMF remain as it is. The second value of PMF is added in the first value and placed over 128. The third value of PMF is added in the second value of CDF , that gives 110/110 which is equal to 1.

And also now , the function is growing monotonically which is necessary condition for histogram equalization.

PMF and CDF usage in histogram equalization

Histogram equalization.

Histogram equalization is discussed in the next tutorial but a brief introduction of histogram equalization is given below.

Histogram equalization is used for enhancing the contrast of the images.

PMF and CDF are both use in histogram equalization as it is described in the beginning of this tutorial. In the histogram equalization , the first and the second step are PMF and CDF. Since in histogram equalization , we have to equalize all the pixel values of an image. So PMF helps us calculating the probability of each pixel value in an image. And CDF gives us the cumulative sum of these values. Further on , this CDF is multiplied by levels , to find the new pixel intensities , which are mapped into old values , and your histogram is equalized.

We have already seen that contrast can be increased using histogram stretching. In this tutorial we will see that how histogram equalization can be used to enhance contrast.

Before performing histogram equalization, you must know two important concepts used in equalizing histograms. These two concepts are known as PMF and CDF.

They are discussed in our tutorial of PMF and CDF. Please visit them in order to successfully grasp the concept of histogram equalization.

Histogram Equalization:

Histogram equalization is used to enhance contrast. It is not necessary that contrast will always be increase in this. There may be some cases were histogram equalization can be worse. In that cases the contrast is decreased.

Lets start histogram equalization by taking this image below as a simple image.

Image

Histogram of this image:

The histogram of this image has been shown below.

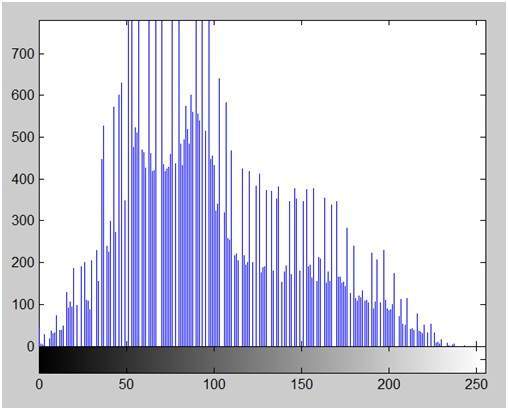
Now we will perform histogram equalization to it.

PMF:

First we have to calculate the PMF (probability mass function) of all the pixels in this image. If you donot know how to calculate PMF, please visit our tutorial of PMF calculation.

CDF:

Our next step involves calculation of CDF (cumulative distributive function). Again if you donot know how to calculate CDF , please visit our tutorial of CDF calculation.

Calculate CDF according to gray levels

Lets for instance consider this , that the CDF calculated in the second step looks like this.

Gray Level Value	CDF
0	0.11
1	0.22
2	0.55
3	0.66
4	0.77
5	0.88
6	0.99
7	1

Then in this step you will multiply the CDF value with (Gray levels (minus) 1) .

Considering we have an 3 bpp image. Then number of levels we have are 8. And 1 subtracts 8 is 7. So we multiply CDF by 7. Here what we got after multiplying.

Gray Level Value	CDF	CDF * (Levels-1)
0	0.11	0
1	0.22	1
2	0.55	3
3	0.66	4
4	0.77	5
5	0.88	6
6	0.99	6
7	1	7

Now we have is the last step , in which we have to map the new gray level values into number of pixels.

Lets assume our old gray levels values has these number of pixels.

Gray Level Value	Frequency
0	2
1	4
2	6
3	8
4	10
5	12
6	14
7	16

Now if we map our new values to , then this is what we got.

Gray Level Value	New Gray Level Value	Frequency
0	0	2
1	1	4
2	3	6
3	4	8
4	5	10
5	6	12
6	6	14
7	7	16

Now map these new values you are onto histogram , and you are done.

Lets apply this technique to our original image. After applying we got the following image and its following histogram.

Histogram Equalization Image

Cumulative Distributive function of this image

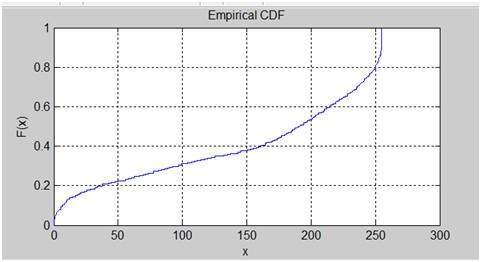
Histogram Equalization histogram

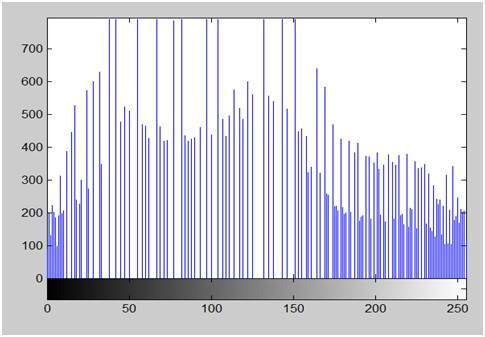
Comparing both the histograms and images

Conclusion

As you can clearly see from the images that the new image contrast has been enhanced and its histogram has also been equalized. There is also one important thing to be note here that during histogram equalization the overall shape of the histogram changes, where as in histogram stretching the overall shape of histogram remains same.

We have discussed some of the basic transformations in our tutorial of Basic transformation. In this tutorial we will look at some of the basic gray level transformations.

Image enhancement

Enhancing an image provides better contrast and a more detailed image as compare to non enhanced image. Image enhancement has very applications. It is used to enhance medical images , images captured in remote sensing , images from satellite e.t.c

The transformation function has been given below

s = T ( r )

where r is the pixels of the input image and s is the pixels of the output image. T is a transformation function that maps each value of r to each value of s. Image enhancement can be done through gray level transformations which are discussed below.

Gray level transformation

There are three basic gray level transformation.

• Linear

• Logarithmic

• Power – law

The overall graph of these transitions has been shown below.

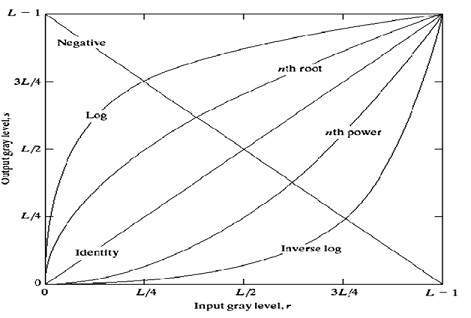
Linear transformation

First we will look at the linear transformation. Linear transformation includes simple identity and negative transformation. Identity transformation has been discussed in our tutorial of image transformation, but a brief description of this transformation has been given here.

Identity transition is shown by a straight line. In this transition, each value of the input image is directly mapped to each other value of output image. That results in the same input image and output image. And hence is called identity transformation. It has been shown below

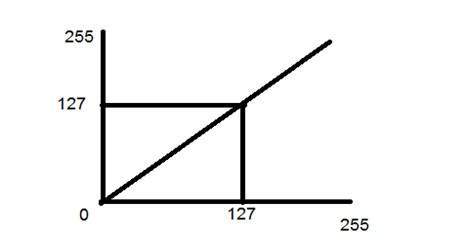
Negative transformation

The second linear transformation is negative transformation, which is invert of identity transformation. In negative transformation, each value of the input image is subtracted from the L-1 and mapped onto the output image.

The result is somewhat like this.

Input Image

Output Image

In this case the following transition has been done.

s = (L – 1) – r

since the input image of Einstein is an 8 bpp image , so the number of levels in this image are 256. Putting 256 in the equation, we get this

s = 255 – r

So each value is subtracted by 255 and the result image has been shown above. So what happens is that , the lighter pixels become dark and the darker picture becomes light. And it results in image negative.

It has been shown in the graph below.

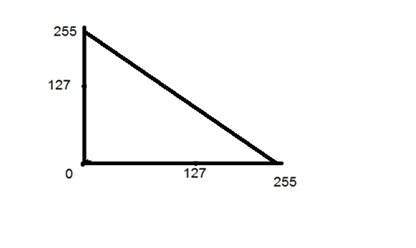
Logarithmic transformations:

Logarithmic transformation further contains two type of transformation. Log transformation and inverse log transformation.

Log transformation

The log transformations can be defined by this formula

s = c log(r + 1).

Where s and r are the pixel values of the output and the input image and c is a constant. The value 1 is added to each of the pixel value of the input image because if there is a pixel intensity of 0 in the image, then log (0) is equal to infinity. So 1 is added , to make the minimum value at least 1.

During log transformation , the dark pixels in an image are expanded as compare to the higher pixel values. The higher pixel values are kind of compressed in log transformation. This result in following image enhancement.

The value of c in the log transform adjust the kind of enhancement you are looking for.

Imagem de entrada

Log Tranform Image

A transformação de log inversa é oposta à transformação de log.

Poder - transformações de lei

Existem mais duas transformações, as transformações de lei de potência, que incluem a enésima potência e a enésima transformação da raiz. Essas transformações podem ser dadas pela expressão:

s = cr ^ γ

Este símbolo γ é denominado gama, devido ao qual esta transformação também é conhecida como transformação gama.

A variação no valor de γ varia o realce das imagens. Dispositivos / monitores de exibição diferentes têm sua própria correção de gama, é por isso que exibem sua imagem em intensidades diferentes.

Este tipo de transformação é usado para aprimorar imagens para diferentes tipos de dispositivos de exibição. A gama de diferentes dispositivos de exibição é diferente. Por exemplo, Gama de CRT está entre 1,8 e 2,5, o que significa que a imagem exibida no CRT está escura.

Corrigindo gama.

s = cr ^ γ

s = cr ^ (1 / 2,5)

A mesma imagem, mas com diferentes valores gama, foi mostrada aqui.

Por exemplo:

Gamma = 10

Gamma = 8

Gamma = 6

Este tutorial é sobre um dos conceitos muito importantes de sinais e sistema. Discutiremos completamente a convolução. O que é isso? Porque é isso? O que podemos conseguir com isso?

Começaremos discutindo a convolução a partir dos fundamentos do processamento de imagem.

O que é processamento de imagem.

Como discutimos na introdução aos tutoriais de processamento de imagem e no sinal e sistema, esse processamento de imagem é mais ou menos o estudo de sinais e sistemas porque uma imagem nada mais é do que um sinal bidimensional.

Também discutimos que, no processamento de imagens, estamos desenvolvendo um sistema cuja entrada é uma imagem e a saída seria uma imagem. Isso é representado pictoricamente como.

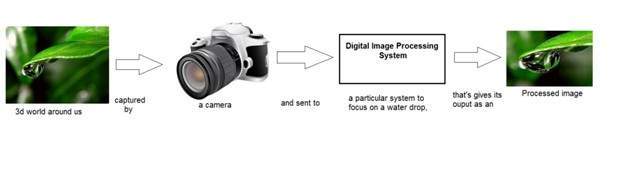
A caixa é a que é mostrada na figura acima rotulada como "Sistema de processamento de imagem digital" pode ser considerada como uma caixa preta

Pode ser melhor representado como:

Onde chegamos até agora

Até agora, discutimos dois métodos importantes para manipular imagens. Ou em outras palavras, podemos dizer que, nossa caixa preta funciona de duas maneiras diferentes até agora.

As duas maneiras diferentes de manipular imagens eram

Graphs (Histograms)

Este método é conhecido como processamento de histograma. Discutimos isso em detalhes em tutoriais anteriores para aumentar o contraste, aprimoramento de imagem, brilho etc.

Transformation functions

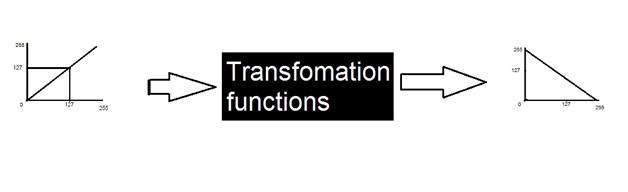
Este método é conhecido como transformações, em que discutimos diferentes tipos de transformações e algumas transformações de nível de cinza

Outra forma de lidar com imagens

Aqui vamos discutir outro método de lidar com imagens. Este outro método é conhecido como convolução. Normalmente, a caixa preta (sistema) usada para processamento de imagem é um sistema LTI ou sistema linear invariante no tempo. Por linear, queremos dizer que tal sistema onde a saída é sempre linear, nem log, nem expoente ou qualquer outro. E por invariante no tempo, queremos dizer um sistema que permanece o mesmo durante o tempo.

Portanto, agora vamos usar este terceiro método. Ele pode ser representado como.

Pode ser representado matematicamente de duas maneiras

g(x,y) = h(x,y) * f(x,y)

Isso pode ser explicado como a “máscara convolvida com uma imagem”.

Ou

g(x,y) = f(x,y) * h(x,y)

Pode ser explicado como “imagem convolvida com máscara”.

Existem duas maneiras de representar isso porque o operador de convolução (*) é comutativo. O h (x, y) é a máscara ou filtro.

O que é máscara?

A máscara também é um sinal. Ele pode ser representado por uma matriz bidimensional. A máscara é geralmente da ordem de 1x1, 3x3, 5x5, 7x7. Uma máscara deve estar sempre em número ímpar, porque do contrário você não conseguirá encontrar o meio da máscara. Por que precisamos encontrar o meio da máscara. A resposta está abaixo, no tópico de, como realizar a convolução?

Como fazer a convolução?

Para realizar a convolução em uma imagem, as seguintes etapas devem ser executadas.

• Vire a máscara (horizontal e verticalmente) apenas uma vez

• Deslize a máscara na imagem.

• Multiplique os elementos correspondentes e, em seguida, adicione-os

• Repita este procedimento até que todos os valores da imagem tenham sido calculados.

Exemplo de convolução

Vamos fazer alguma convolução. A etapa 1 é virar a máscara.

Mascarar:

Vamos usar nossa máscara para ser isso.

1	2	3
4	5	6
7	8	9

Virando a máscara horizontalmente

3	2	1
6	5	4
9	8	7

Virando a máscara verticalmente

9	8	7
6	5	4
3	2	1

Imagem:

Vamos considerar uma imagem como esta

2	4	6
8	10	12
14	16	18

Convolução

Máscara convolvente sobre imagem. É feito dessa maneira. Coloque o centro da máscara em cada elemento de uma imagem. Multiplique os elementos correspondentes e, em seguida, adicione-os e cole o resultado no elemento da imagem em que você posiciona o centro da máscara.

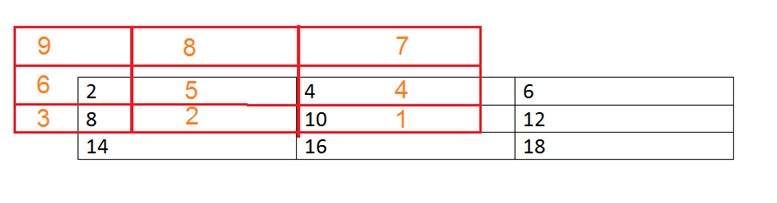
A caixa em vermelho é a máscara e os valores em laranja são os valores da máscara. A caixa preta e os valores pertencem à imagem. Agora, para o primeiro pixel da imagem, o valor será calculado como

Primeiro pixel = (5 * 2) + (4 * 4) + (2 * 8) + (1 * 10)

= 10 + 16 + 16 + 10

= 52

Coloque 52 na imagem original no primeiro índice e repita este procedimento para cada pixel da imagem.

Por que convolução

A convolução pode realizar algo que os dois métodos anteriores de manipulação de imagens não conseguem. Isso inclui desfoque, nitidez, detecção de bordas, redução de ruído, etc.

O que é uma máscara.

Uma máscara é um filtro. O conceito de mascaramento também é conhecido como filtragem espacial. O mascaramento também é conhecido como filtragem. Neste conceito tratamos apenas da operação de filtragem que é realizada diretamente na imagem.

Um exemplo de máscara foi mostrado abaixo

-1	0	1
-1	0	1
-1	0	1

O que é filtragem.

O processo de filtragem também é conhecido como convolução de uma máscara com uma imagem. Como este processo é igual ao da convolução, as máscaras de filtro também são conhecidas como máscaras de convolução.

Como isso é feito.

O processo geral de filtragem e aplicação de máscaras consiste em mover a máscara de filtro de ponto a ponto em uma imagem. Em cada ponto (x, y) da imagem original, a resposta de um filtro é calculada por uma relação pré-definida. Todos os valores dos filtros são pré-definidos e são um padrão.

Tipos de filtros

Geralmente, existem dois tipos de filtros. Um é chamado de filtros lineares ou filtros de suavização e outros são chamados de filtros de domínio de frequência.

Por que filtros são usados?

Os filtros são aplicados na imagem para várias finalidades. Os dois usos mais comuns são os seguintes:

• Filtros são usados ​​para desfoque e redução de ruído

• Filtros são usados ​​ou detecção de borda e nitidez

Desfoque e redução de ruído:

Os filtros são mais comumente usados ​​para desfoque e redução de ruído. O desfoque é usado nas etapas de pré-processamento, como a remoção de pequenos detalhes de uma imagem antes da extração de objetos grandes.

Máscaras para desfoque.

As máscaras comuns para desfoque são.

• Filtro de caixa

• Filtro de média ponderada

No processo de desfoque, reduzimos o conteúdo da borda em uma imagem e tentamos fazer as transições entre diferentes intensidades de pixel o mais suaves possível.

A redução de ruído também é possível com a ajuda de desfoque.

Detecção de bordas e nitidez:

Máscaras ou filtros também podem ser usados ​​para detecção de bordas em uma imagem e para aumentar a nitidez de uma imagem.

Quais são as arestas.

Também podemos dizer que mudanças repentinas de descontinuidades em uma imagem são chamadas de arestas. As transições significativas em uma imagem são chamadas de bordas. Uma imagem com bordas é mostrada abaixo.

Imagem original.

Mesma imagem com bordas

Uma breve introdução sobre desfoque foi discutida em nosso tutorial anterior sobre o conceito de máscaras, mas vamos discutir isso formalmente aqui.

Borrar

No desfoque, simplesmente desfocamos uma imagem. Uma imagem parece mais nítida ou detalhada se formos capazes de perceber todos os objetos e suas formas corretamente. Por exemplo. Uma imagem com um rosto, parece nítida quando conseguimos identificar olhos, orelhas, nariz, lábios, testa etc muito nítidos. Esta forma de um objeto se deve às suas bordas. Assim, no desfoque, simplesmente reduzimos o conteúdo da borda e tornamos a transição de uma cor para a outra muito suave.

Desfoque vs zoom.

Você pode ter visto uma imagem borrada ao ampliar uma imagem. Quando você aplica zoom em uma imagem usando replicação de pixels e o fator de zoom é aumentado, você vê uma imagem borrada. Esta imagem também tem menos detalhes, mas não é um borrão verdadeiro.

Porque no zoom, você adiciona novos pixels a uma imagem, o que aumenta o número geral de pixels em uma imagem, enquanto no desfoque, o número de pixels de uma imagem normal e de uma imagem desfocada permanece o mesmo.

Exemplo comum de imagem desfocada.

Tipos de filtros.

O desfoque pode ser obtido de várias maneiras. Os tipos comuns de filtros usados ​​para desfocar são.

• Filtro médio

• Filtro de média ponderada

• Filtro gaussiano

Destes três, vamos discutir os dois primeiros aqui e Gaussiano será discutido mais tarde nos próximos tutoriais.

Filtro médio.

O filtro de média também é conhecido como filtro de caixa e filtro de média. Um filtro médio possui as seguintes propriedades.

• Deve ser pedido estranho

• A soma de todos os elementos deve ser 1

• Todos os elementos devem ser iguais

Se seguirmos esta regra, então para uma máscara de 3x3. Obtemos o seguinte resultado.

1/9	1/9	1/9
1/9	1/9	1/9
1/9	1/9	1/9

Por ser uma máscara 3x3, isso significa que tem 9 células. A condição de que toda a soma do elemento seja igual a 1 pode ser alcançada dividindo cada valor por 9. Como

1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 + 1/9 = 9/9 = 1

O resultado de uma máscara de 3x3 em uma imagem é mostrado abaixo.

Imagem original:

Imagem borrada

Pode ser que os resultados não sejam muito claros. Vamos aumentar o desfoque. O desfoque pode ser aumentado aumentando o tamanho da máscara. Quanto maior for o tamanho da máscara, maior será o desfoque. Porque com uma máscara maior, um maior número de pixels é fornecido e uma transição suave é definida.

O resultado de uma máscara de 5x5 em uma imagem é mostrado abaixo.

Imagem original:

Imagem borrada:

Da mesma forma, se aumentarmos a máscara, o desfoque seria maior e os resultados são mostrados abaixo.

O resultado de uma máscara de 7x7 em uma imagem é mostrado abaixo.

Imagem original:

Imagem borrada:

O resultado de uma máscara de 9x9 em uma imagem é mostrado abaixo.

Imagem original:

Imagem borrada:

O resultado de uma máscara de 11x11 em uma imagem é mostrado abaixo.

Imagem original:

Imagem borrada:

Filtro de média ponderada.

No filtro de média ponderada, atribuímos mais peso ao valor central. Devido a que a contribuição do centro se torna mais do que o resto dos valores. Devido à filtragem de média ponderada, podemos realmente controlar o desfoque.

As propriedades do filtro de média ponderada são.

• Deve ser pedido estranho

• A soma de todos os elementos deve ser 1

• O peso do elemento central deve ser mais do que todos os outros elementos

Filtro 1

1	1	1
1	2	1
1	1	1

As duas propriedades são satisfeitas, que são (1 e 3). Mas a propriedade 2 não está satisfeita. Então, para satisfazer isso, vamos simplesmente dividir o filtro inteiro por 10, ou multiplicá-lo por 1/10.

Filtro 2

1	1	1
1	10	1
1	1	1

Fator de divisão = 18.

Discutimos brevemente sobre a detecção de bordas em nosso tutorial de introdução às máscaras. Discutiremos formalmente a detecção de bordas aqui.

Quais são as arestas.

Também podemos dizer que mudanças repentinas de descontinuidades em uma imagem são chamadas de arestas. As transições significativas em uma imagem são chamadas de bordas.

Tipos de arestas.

Geralmente as bordas são de três tipos:

• Arestas horizontais

• Bordas Verticais

• Bordas Diagonais

Por que detectar bordas.

A maior parte das informações de formato de uma imagem é delimitada por bordas. Portanto, primeiro detectamos essas bordas em uma imagem e usando esses filtros e, em seguida, aprimorando as áreas da imagem que contêm bordas, a nitidez da imagem aumentará e a imagem se tornará mais clara.

Aqui estão algumas das máscaras para detecção de bordas que discutiremos nos próximos tutoriais.

• Operador Prewitt

• Operador Sobel

• Robinson Compass Masks

• Krisch Compass Masks

• Operador Laplaciano.

Acima mencionados, todos os filtros são filtros lineares ou filtros de suavização.

Operador Prewitt

O operador Prewitt é usado para detectar bordas horizontalmente e verticalmente.

Operador Sobel

O operador sobel é muito semelhante ao operador Prewitt. Também é uma máscara derivada e é usada para detecção de bordas. Ele também calcula arestas nas direções horizontal e vertical.

Robinson Compass Masks

Este operador também é conhecido como máscara de direção. Neste operador, pegamos uma máscara e a giramos em todas as 8 direções principais da bússola para calcular as bordas de cada direção.

Máscaras Kirsch Compass

Kirsch Compass Mask também é uma máscara derivada que é usada para encontrar bordas. A máscara de Kirsch também é usada para calcular arestas em todas as direções.

Operador Laplaciano.

Operador Laplaciano também é um operador derivado que é usado para localizar bordas em uma imagem. Laplaciano é uma máscara derivada de segunda ordem. Ele pode ser dividido em laplaciano positivo e laplaciano negativo.

Todas essas máscaras encontram bordas. Alguns encontram horizontalmente e verticalmente, alguns encontram em apenas uma direção e alguns encontram em todas as direções. O próximo conceito que vem depois disso é o de nitidez, que pode ser feito assim que as bordas forem extraídas da imagem

Nitidez:

A nitidez é oposta ao embaçamento. No desfoque, reduzimos o conteúdo da borda e, em sharpneng, aumentamos o conteúdo da borda. Portanto, para aumentar o conteúdo das bordas em uma imagem, temos que encontrar as bordas primeiro.

As bordas podem ser encontradas por um dos métodos descritos acima, usando qualquer operador. Depois de encontrar as bordas, adicionaremos essas bordas a uma imagem e, assim, a imagem terá mais bordas e parecerá mais nítida.

Esta é uma forma de tornar uma imagem mais nítida.

A imagem nítida é mostrada abaixo.

Imagem original

Imagem Nítida

O operador Prewitt é usado para detecção de bordas em uma imagem. Ele detecta dois tipos de bordas:

• Arestas horizontais

• Bordas Verticais

As bordas são calculadas usando a diferença entre as intensidades de pixel correspondentes de uma imagem. Todas as máscaras usadas para detecção de bordas também são conhecidas como máscaras derivadas. Porque, como afirmamos muitas vezes antes nesta série de tutoriais, essa imagem também é um sinal, então as mudanças em um sinal só podem ser calculadas usando a diferenciação. É por isso que esses operadores também são chamados de operadores derivados ou máscaras derivadas.

Todas as máscaras derivadas devem ter as seguintes propriedades:

• O sinal oposto deve estar presente na máscara.

• A soma da máscara deve ser igual a zero.

• Mais peso significa mais detecção de bordas.

O operador Prewitt nos fornece duas máscaras, uma para detectar bordas na direção horizontal e outra para detectar bordas na direção vertical.

Direção vertical:

-1	0	1
-1	0	1
-1	0	1

Acima da máscara encontrará as arestas na direção vertical e é porque a coluna de zeros na direção vertical. Quando você vai convolver esta máscara em uma imagem, ela lhe dará as bordas verticais em uma imagem.

Como funciona:

Quando aplicamos esta máscara na imagem, ela destaca bordas verticais. Ele simplesmente funciona como uma derivada de primeira ordem e calcula a diferença de intensidades de pixel em uma região de borda. Como a coluna central é zero, ela não inclui os valores originais de uma imagem, mas sim calcula a diferença entre os valores dos pixels direito e esquerdo em torno dessa borda. Isso aumenta a intensidade da borda e torna-se melhorada comparativamente à imagem original.

Direção horizontal:

-1	-1	-1
0	0	0
1	1	1

A máscara acima encontrará arestas na direção horizontal e é porque essa coluna de zeros está na direção horizontal. Quando você vai convolver esta máscara em uma imagem, ela criaria bordas horizontais proeminentes na imagem.

Como funciona:

Essa máscara destacará as bordas horizontais de uma imagem. Ele também funciona com o princípio da máscara acima e calcula a diferença entre as intensidades de pixel de uma borda específica. Como a linha central da máscara consiste em zeros, ela não inclui os valores originais da borda da imagem, mas sim calcula a diferença das intensidades de pixel acima e abaixo da borda particular. Aumentando assim a mudança repentina de intensidades e tornando a borda mais visível. Ambas as máscaras acima seguem o princípio da máscara derivada. Ambas as máscaras têm sinal oposto e a soma de ambas as máscaras é igual a zero. A terceira condição não será aplicável neste operador, pois ambas as máscaras acima são padronizadas e não podemos alterar o valor nelas.

Agora é hora de ver essas máscaras em ação:

Imagem de amostra:

A seguir está um exemplo de imagem na qual aplicaremos as duas máscaras acima, uma de cada vez.

Depois de aplicar a Máscara Vertical:

Após aplicar a máscara vertical na imagem de amostra acima, a imagem a seguir será obtida. Esta imagem contém bordas verticais. Você pode julgá-lo mais corretamente comparando com a imagem de bordas horizontais.

Depois de aplicar a máscara horizontal:

Depois de aplicar a máscara horizontal na imagem de amostra acima, a imagem a seguir será obtida.

Comparação:

Como você pode ver, na primeira imagem em que aplicamos a máscara vertical, todas as arestas verticais são mais visíveis do que a imagem original. Da mesma forma, na segunda imagem aplicamos a máscara horizontal e, como resultado, todas as arestas horizontais são visíveis. Portanto, desta forma você pode ver que podemos detectar as bordas horizontais e verticais de uma imagem.

O operador sobel é muito semelhante ao operador Prewitt. Também é uma máscara derivada e é usada para detecção de bordas. Como o operador Prewitt, o operador sobel também é usado para detectar dois tipos de bordas em uma imagem:

• Direção vertical

• Direção horizontal

Diferença com o operador Prewitt:

A principal diferença é que no operador sobel os coeficientes das máscaras não são fixos e podem ser ajustados de acordo com nossa exigência, a menos que não violem nenhuma propriedade das máscaras derivadas.

A seguir está a máscara vertical do Operador Sobel:

-1	0	1
-2	0	2
-1	0	1

Esta máscara funciona exatamente da mesma forma que a máscara vertical do operador Prewitt. Há apenas uma diferença: ele possui valores “2” e “-2” no centro da primeira e da terceira colunas. Quando aplicada a uma imagem, essa máscara destacará as bordas verticais.

Como funciona:

Quando aplicamos esta máscara na imagem, ela destaca bordas verticais. Ele simplesmente funciona como uma derivada de primeira ordem e calcula a diferença de intensidades de pixel em uma região de borda.

Como a coluna central é zero, ela não inclui os valores originais de uma imagem, mas sim calcula a diferença entre os valores dos pixels direito e esquerdo em torno dessa borda. Além disso, os valores centrais da primeira e da terceira coluna são 2 e -2, respectivamente.

Isso dá mais peso aos valores de pixel ao redor da região da borda. Isso aumenta a intensidade da borda e torna-se melhorada comparativamente à imagem original.

A seguir está a máscara horizontal do Operador Sobel:

-1	-2	-1
0	0	0
1	2	1

A máscara acima encontrará arestas na direção horizontal e é porque essa coluna de zeros está na direção horizontal. Quando você vai convolver esta máscara em uma imagem, ela criaria bordas horizontais proeminentes na imagem. A única diferença entre ele é que ele tem 2 e -2 como um elemento central da primeira e terceira linhas.

Como funciona:

Essa máscara destacará as bordas horizontais de uma imagem. Ele também funciona com o princípio da máscara acima e calcula a diferença entre as intensidades de pixel de uma borda específica. Como a linha central da máscara consiste em zeros, ela não inclui os valores originais da borda da imagem, mas sim calcula a diferença das intensidades de pixel acima e abaixo da borda particular. Aumentando assim a mudança repentina de intensidades e tornando a borda mais visível.

Agora é hora de ver essas máscaras em ação:

Imagem de amostra:

A seguir está um exemplo de imagem na qual aplicaremos as duas máscaras acima, uma de cada vez.

Depois de aplicar a Máscara Vertical:

Após aplicar a máscara vertical na imagem de amostra acima, a imagem a seguir será obtida.

Depois de aplicar a máscara horizontal:

Depois de aplicar a máscara horizontal na imagem de amostra acima, a imagem a seguir será obtida

Comparação:

Como você pode ver, na primeira imagem em que aplicamos a máscara vertical, todas as arestas verticais são mais visíveis do que a imagem original. Da mesma forma, na segunda imagem aplicamos a máscara horizontal e, como resultado, todas as arestas horizontais são visíveis.

Portanto, desta forma você pode ver que podemos detectar as bordas horizontais e verticais de uma imagem. Além disso, se você comparar o resultado do operador sobel com o operador Prewitt, descobrirá que o operador sobel encontra mais arestas ou torna as arestas mais visíveis em comparação com o operador Prewitt.

Isso ocorre porque no operador sobel atribuímos mais peso às intensidades de pixel ao redor das bordas.

Aplicando mais peso à máscara

Agora também podemos ver que, se aplicarmos mais peso à máscara, mais arestas ela terá para nós. Além disso, conforme mencionado no início do tutorial, não há coeficientes fixos no operador sobel, então aqui está outro operador ponderado

-1	0	1
-5	0	5
-1	0	1

Se você puder comparar o resultado desta máscara com o da máscara vertical de Prewitt, é claro que esta máscara apresentará mais arestas em comparação com a de Prewitt apenas porque colocamos mais peso na máscara.

As máscaras de bússola Robinson são outro tipo de máscara derrivate que é usada para detecção de bordas. Este operador também é conhecido como máscara de direção. Neste operador, pegamos uma máscara e a giramos em todas as 8 direções principais da bússola que são as seguintes:

• North

• noroeste

• West

• Sudoeste

• South

• Sudeste

• East

• Nordeste

Não há máscara fixa. Você pode pegar qualquer máscara e girá-la para encontrar as bordas em todas as direções mencionadas acima. Todas as máscaras são giradas com base na direção de colunas zero.

Por exemplo, vamos ver a seguinte máscara que está na Direção Norte e depois girá-la para fazer todas as máscaras de direção.

Máscara de direção norte

-1	0	1
-2	0	2
-1	0	1

Máscara de direção noroeste

0	1	2
-1	0	1
-2	-1	0

Máscara de direção oeste

1	2	1
0	0	0
-1	-2	-1

Máscara de direção sudoeste

2	1	0
1	0	-1
0	-1	-2

Máscara de direção sul

1	0	-1
2	0	-2
1	0	-1

Máscara de direção sudeste

0	-1	-2
1	0	-1
2	1	0

Máscara de direção leste

-1	-2	-1
0	0	0
1	2	1

Máscara de direção nordeste

-2	-1	0
-1	0	1
0	1	2

Como você pode ver, todas as direções são abordadas com base na direção de zeros. Cada máscara fornecerá as bordas em sua direção. Agora vamos ver o resultado de todas as máscaras acima. Suponha que temos uma imagem de amostra da qual temos que encontrar todas as arestas. Aqui está nossa imagem de exemplo:

Imagem de amostra:

Agora vamos aplicar todos os filtros acima nesta imagem e obter o seguinte resultado.

Bordas de direção norte

Bordas de direção noroeste

Bordas de direção oeste

Bordas de direção sudoeste

Bordas da direção sul

Bordas de direção sudeste

Bordas da direção leste

Bordas de direção nordeste

Como você pode ver, ao aplicar todas as máscaras acima, você obterá bordas em todas as direções. O resultado também depende da imagem. Suponha que haja uma imagem, que não tem nenhuma borda de direção Nordeste, então essa máscara será ineficaz.

Kirsch Compass Mask também é uma máscara derivada que é usada para encontrar bordas. Isso também é como a bússola de Robinson encontrar bordas em todas as oito direções de uma bússola. A única diferença entre as máscaras de bússola Robinson e kirsch é que em Kirsch temos uma máscara padrão, mas em Kirsch mudamos a máscara de acordo com nossos próprios requisitos.

Com a ajuda de Kirsch Compass Masks, podemos encontrar arestas nas seguintes oito direções.

• North

• noroeste

• West

• Sudoeste

• South

• Sudeste

• East

• Nordeste

Pegamos uma máscara padrão que segue todas as propriedades de uma máscara derivada e a giramos para encontrar as arestas.

Por exemplo, vamos ver a seguinte máscara que está na Direção Norte e depois girá-la para fazer todas as máscaras de direção.

Máscara de direção norte

-3	-3	5
-3	0	5
-3	-3	5

Máscara de direção noroeste

-3	5	5
-3	0	5
-3	-3	-3

Máscara de direção oeste

5	5	5
-3	0	-3
-3	-3	-3

Máscara de direção sudoeste

5	5	-3
5	0	-3
-3	-3	-3

Máscara de direção sul

5	-3	-3
5	0	-3
5	-3	-3

Máscara de direção sudeste

-3	-3	-3
5	0	-3
5	5	-3

Máscara de direção leste

-3	-3	-3
-3	0	-3
5	5	5

Máscara de direção nordeste

-3	-3	-3
-3	0	5
-3	5	5

Como você pode ver, todas as direções estão cobertas e cada máscara fornecerá as bordas de sua própria direção. Agora, para ajudá-lo a entender melhor o conceito dessas máscaras, vamos aplicá-lo em uma imagem real. Suponha que temos uma imagem de amostra da qual temos que encontrar todas as arestas. Aqui está nossa imagem de exemplo:

Imagem de amostra

Agora vamos aplicar todos os filtros acima nesta imagem e obter o seguinte resultado.

Bordas de direção norte

Bordas de direção noroeste

Bordas de direção oeste

Bordas de direção sudoeste

Bordas da direção sul

Bordas de direção sudeste

Bordas da direção leste

Bordas de direção nordeste

Como você pode ver, ao aplicar todas as máscaras acima, você obterá bordas em todas as direções. O resultado também depende da imagem. Suponha que haja uma imagem, que não tem nenhuma borda de direção Nordeste, então essa máscara será ineficaz.

Operador Laplaciano também é um operador derivado que é usado para localizar bordas em uma imagem. A principal diferença entre o Laplaciano e outros operadores como Prewitt, Sobel, Robinson e Kirsch é que todos são máscaras derivadas de primeira ordem, mas o Laplaciano é uma máscara derivada de segunda ordem. Nesta máscara, temos duas classificações adicionais, uma é Operador Laplaciano Positivo e a outra é Operador Laplaciano Negativo.

Outra diferença entre o Laplaciano e outros operadores é que, ao contrário de outros operadores, o Laplaciano não remove arestas em nenhuma direção específica, mas remove arestas na classificação seguinte.

• Bordas Internas

• Bordas Externas

Vamos ver como funciona o operador Laplaciano.

Operador Laplaciano Positivo:

No Laplaciano Positivo, temos uma máscara padrão em que o elemento central da máscara deve ser negativo e os elementos de canto da máscara devem ser zero.

0	1	0
1	-4	1
0	1	0

O Operador Laplaciano Positivo é usado para remover as bordas externas de uma imagem.

Operador Laplaciano Negativo:

No operador Laplaciano negativo, também temos uma máscara padrão, na qual o elemento central deve ser positivo. Todos os elementos no canto devem ser zero e o restante de todos os elementos na máscara deve ser -1.

0	-1	0
-1	4	-1
0	-1	0

O operador Laplaciano negativo é usado para retirar as bordas internas de uma imagem

Como funciona:

Laplaciano é um operador derivado; seus usos destacam as descontinuidades de nível de cinza em uma imagem e tentam diminuir a ênfase nas regiões com níveis de cinza que variam lentamente. Esta operação em resultado produz tais imagens que têm linhas de borda acinzentadas e outras descontinuidades em um fundo escuro. Isso produz bordas internas e externas em uma imagem

O importante é como aplicar esses filtros na imagem. Lembre-se de que não podemos aplicar o operador Laplaciano positivo e negativo na mesma imagem. temos que aplicar apenas um, mas o que devemos lembrar é que, se aplicarmos o operador Laplaciano positivo à imagem, subtrairemos a imagem resultante da imagem original para obter a imagem mais nítida. Da mesma forma, se aplicarmos o operador Laplaciano negativo, temos que adicionar a imagem resultante na imagem original para obter a imagem mais nítida.

Vamos aplicar esses filtros a uma imagem e ver como eles nos levarão para dentro e para fora de uma imagem. Suponha que temos uma imagem de amostra a seguir.

Imagem de amostra

After applying Positive Laplacian Operator:

Depois de aplicar o operador Laplaciano positivo, obteremos a seguinte imagem.

After applying Negative Laplacian Operator:

Depois de aplicar o operador Laplaciano negativo, obteremos a seguinte imagem.

Temos lidado com imagens em muitos domínios. Agora estamos processando sinais (imagens) no domínio da frequência. Como esta série de Fourier e o domínio da frequência são puramente matemáticos, tentaremos minimizar a parte matemática e nos concentrar mais em seu uso no DIP.

Análise de domínio de frequência

Até agora, todos os domínios em que analisamos um sinal, o analisamos em relação ao tempo. Mas no domínio da frequência não analisamos o sinal em relação ao tempo, mas sim em relação à frequência.

Diferença entre domínio espacial e domínio da frequência.

No domínio espacial, lidamos com as imagens como elas são. O valor dos pixels da imagem muda em relação à cena. Enquanto no domínio da frequência, lidamos com a taxa na qual os valores dos pixels estão mudando no domínio espacial.

Para simplificar, vamos colocar desta forma.

Spatial domain

No domínio espacial simples, lidamos diretamente com a matriz da imagem. Já no domínio da frequência, lidamos com uma imagem como esta.

Domínio de frequência

Primeiro transformamos a imagem em sua distribuição de frequência. Em seguida, nosso sistema de caixa preta executa todo o processamento que precisa ser executado, e a saída da caixa preta, neste caso, não é uma imagem, mas uma transformação. Após realizar a transformação inversa, ele é convertido em uma imagem que é então visualizada no domínio espacial.

Pode ser visto pictoricamente como

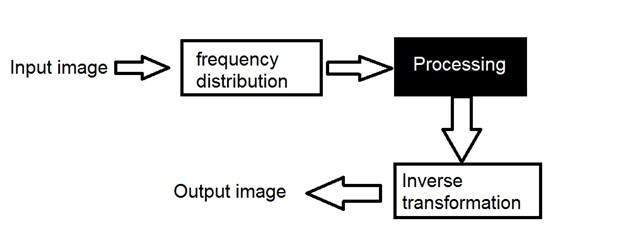
Aqui, usamos a palavra transformação. O que isso realmente significa?

Transformação.

Um sinal pode ser convertido do domínio do tempo para o domínio da frequência usando operadores matemáticos chamados de transformações. Existem muitos tipos de transformação que fazem isso. Alguns deles são fornecidos abaixo.

• Séries de Fourier

• Transformação de Fourier

• Transformada de Laplace

• Transformada Z

De tudo isso, discutiremos exaustivamente a série Fourier e a transformação de Fourier em nosso próximo tutorial.

Componentes de freqüência

Qualquer imagem no domínio espacial pode ser representada no domínio da frequência. Mas o que essas frequências realmente significam.

Vamos dividir os componentes de frequência em dois componentes principais.

High frequency components

Os componentes de alta frequência correspondem às bordas de uma imagem.

Low frequency components

Os componentes de baixa frequência em uma imagem correspondem a regiões suaves.

No último tutorial de análise no domínio da frequência, discutimos que a série de Fourier e a transformada de Fourier são usadas para converter um sinal no domínio da frequência.

Fourier

Fourier foi um matemático em 1822. Ele deu a série de Fourier e a transformada de Fourier para converter um sinal no domínio da frequência.

Fourier Series

A série de Fourier simplesmente afirma que os sinais periódicos podem ser representados na soma de senos e cossenos quando multiplicados por um certo peso. Além disso, afirma que os sinais periódicos podem ser divididos em outros sinais com as seguintes propriedades.

• Os sinais são senos e cossenos

• Os sinais são harmônicos entre si

Pode ser visto pictoricamente como

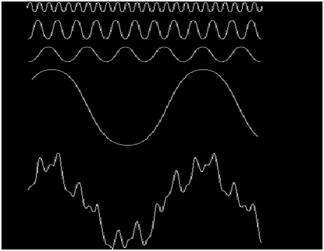
No sinal acima, o último sinal é na verdade a soma de todos os sinais acima. Essa foi a ideia do Fourier.

Como é calculado.

Já que, como vimos no domínio da frequência, para processar uma imagem no domínio da frequência, precisamos primeiro convertê-la usando no domínio da frequência e temos que tomar o inverso da saída para convertê-la de volta no domínio espacial. É por isso que a série de Fourier e a transformação de Fourier têm duas fórmulas. Um para conversão e outro para convertê-lo de volta ao domínio espacial.

Séries de Fourier

A série de Fourier pode ser denotada por esta fórmula.

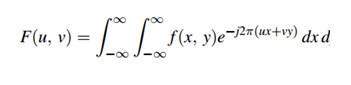
O inverso pode ser calculado por esta fórmula.

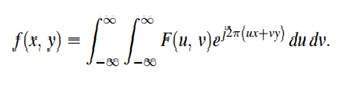
transformada de Fourier

A transformada de Fourier simplesmente afirma que os sinais não periódicos cuja área sob a curva é finita também podem ser representados em integrais dos senos e cossenos após serem multiplicados por um certo peso.

A transformada de Fourier tem muitas aplicações amplas que incluem compressão de imagem (por exemplo, compressão JPEG), filtragem e análise de imagem.

Diferença entre a série de Fourier e a transformada

Embora a série de Fourier e a transformada de Fourier sejam fornecidas por Fourier, a diferença entre elas é que a série de Fourier é aplicada em sinais periódicos e a transformada de Fourier é aplicada em sinais não periódicos

Qual deles é aplicado nas imagens.

Agora a questão é qual deles é aplicado às imagens, a série de Fourier ou a transformada de Fourier. Bem, a resposta a esta pergunta reside no fato de que o que são as imagens. As imagens não são periódicas. E como as imagens não são periódicas, a transformada de Fourier é usada para convertê-las no domínio da frequência.

Transformada discreta de Fourier.

Como estamos lidando com imagens, e de fato imagens digitais, para imagens digitais estaremos trabalhando com transformada discreta de Fourier

Considere o termo de Fourier acima para uma sinusóide. Inclui três coisas.

• Frequência Espacial

• Magnitude

• Phase

A frequência espacial se relaciona diretamente com o brilho da imagem. A magnitude da sinusóide está diretamente relacionada com o contraste. O contraste é a diferença entre a intensidade máxima e mínima do pixel. Fase contém as informações de cor.

A fórmula para a transformada discreta de Fourier bidimensional é fornecida abaixo.

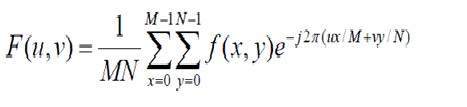
A transformada discreta de Fourier é, na verdade, a transformada de Fourier amostrada, portanto, contém algumas amostras que denotam uma imagem. Na fórmula acima, f (x, y) denota a imagem e F (u, v) denota a transformada discreta de Fourier. A fórmula para a transformada discreta inversa de Fourier bidimensional é fornecida abaixo.

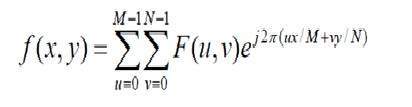
A transformada discreta de Fourier inversa converte a transformada de Fourier de volta à imagem

Considere este sinal.

Agora veremos uma imagem, da qual calcularemos o espectro de magnitude FFT e, em seguida, o espectro de magnitude FFT deslocado e então tomaremos o Log desse espectro deslocado.

Imagem original

O espectro de magnitude da transformada de Fourier

A transformada deslocada de Fourier

O Espectro de Magnitude Deslocado

No último tutorial, discutimos sobre as imagens no domínio da frequência. Neste tutorial, vamos definir uma relação entre o domínio da frequência e as imagens (domínio espacial).

Por exemplo:

Considere este exemplo.

A mesma imagem no domínio da frequência pode ser representada como.

Agora, qual é a relação entre imagem ou domínio espacial e domínio da frequência. Esta relação pode ser explicada por um teorema que é chamado de teorema da convolução.

Teorema da Convolução

A relação entre o domínio espacial e o domínio da frequência pode ser estabelecida pelo teorema da convolução.

O teorema da convolução pode ser representado como.

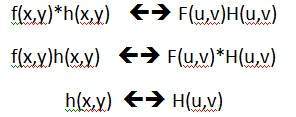
Pode-se afirmar que a convolução no domínio espacial é igual à filtragem no domínio da frequência e vice-versa.

A filtragem no domínio da frequência pode ser representada da seguinte forma:

The steps in filtering are given below.

• Na primeira etapa temos que fazer um pré-processamento de uma imagem no domínio espacial, para aumentar seu contraste ou brilho

• Em seguida, tomaremos a transformada discreta de Fourier da imagem

• Em seguida, centralizaremos a transformada discreta de Fourier, pois traremos a transformada discreta de Fourier no centro dos cantos

• Então vamos aplicar a filtragem, significa que vamos multiplicar a transformada de Fourier por uma função de filtro

• Em seguida, iremos novamente deslocar o DFT do centro para os cantos

• A última etapa seria realizar a transformada discreta de Fourier inversa, para trazer o resultado de volta do domínio da frequência para o domínio espacial

• E essa etapa do pós-processamento é opcional, assim como o pré-processamento, no qual apenas aumentamos a aparência da imagem.

Filtros

O conceito de filtro no domínio da frequência é igual ao conceito de máscara em convolução.

Depois de converter uma imagem para o domínio da frequência, alguns filtros são aplicados no processo de filtragem para realizar diferentes tipos de processamento em uma imagem. O processamento inclui borrar uma imagem, aumentar a nitidez de uma imagem, etc.

Os tipos comuns de filtros para essas finalidades são:

• Filtro passa-alto ideal

• Filtro passa-baixo ideal

• Filtro passa-alto gaussiano

• Filtro passa-baixo gaussiano

No próximo tutorial, discutiremos sobre filtro em detalhes.

No último tutorial, discutimos brevemente sobre filtros. Neste tutorial, discutiremos detalhadamente sobre eles. Antes de discutir, vamos primeiro falar sobre máscaras. O conceito de máscara foi discutido em nosso tutorial de convolução e máscaras.

Máscaras borradas vs máscaras derivadas.

Faremos uma comparação entre máscaras de desfoque e máscaras derivadas.

Máscaras embaçadas:

Uma máscara de desfoque tem as seguintes propriedades.

• Todos os valores nas máscaras de desfoque são positivos

• A soma de todos os valores é igual a 1

• O conteúdo da borda é reduzido usando uma máscara de desfoque

• Conforme o tamanho da máscara aumenta, mais efeito de suavização ocorrerá

Máscaras Derrivativas:

Uma máscara derivada possui as seguintes propriedades.

• Uma máscara derivada tem valores positivos e negativos

• A soma de todos os valores em uma máscara derivada é igual a zero

• O conteúdo da borda é aumentado por uma máscara derivada

• Conforme o tamanho da máscara aumenta, mais conteúdo de borda é aumentado

Relação entre máscara de desfoque e máscara derivada com filtros passa-altas e filtros passa-baixas.

A relação entre a máscara de desfoque e a máscara derivada com um filtro passa-alta e um filtro passa-baixa pode ser definida simplesmente como.

• Máscaras de borrão também são chamadas de filtro passa-baixo

• Máscaras derivadas também são chamadas de filtro passa-alto

Componentes de frequência passa-alto e componentes de frequência passa-baixo

The high pass frequency components denotes edges whereas the low pass frequency components denotes smooth regions.

Ideal low pass and Ideal High pass filters

This is the common example of low pass filter.

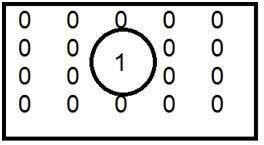
When one is placed inside and the zero is placed outside , we got a blurred image. Now as we increase the size of 1, blurring would be increased and the edge content would be reduced.

This is a common example of high pass filter.

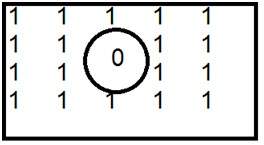
When 0 is placed inside, we get edges , which gives us a sketched image. An ideal low pass filter in frequency domain is given below

The ideal low pass filter can be graphically represented as

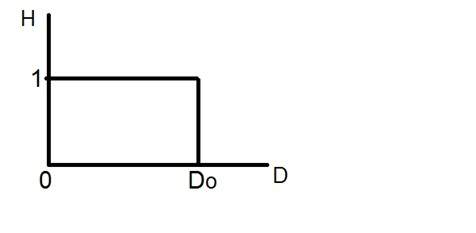
Now let’s apply this filter to an actual image and let’s see what we got.

Sample image.

Image in frequency domain

Applying filter over this image

Resultant Image

With the same way , an ideal high pass filter can be applied on an image. But obviously the results would be different as , the low pass reduces the edged content and the high pass increase it.

Gaussian Low pass and Gaussian High pass filter

Gaussian low pass and Gaussian high pass filter minimize the problem that occur in ideal low pass and high pass filter.

This problem is known as ringing effect. This is due to reason because at some points transition between one color to the other cannot be defined precisely, due to which the ringing effect appears at that point.

Have a look at this graph.

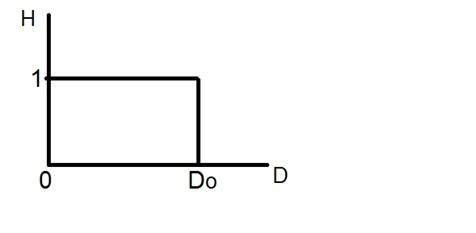
This is the representation of ideal low pass filter. Now at the exact point of Do , you cannot tell that the value would be 0 or 1. Due to which the ringing effect appears at that point.

So in order to reduce the effect that appears is ideal low pass and ideal high pass filter , the following Gaussian low pass filter and Gaussian high pass filter is introduced.

Gaussian Low pass filter

The concept of filtering and low pass remains the same, but only the transition becomes different and become more smooth.

The Gaussian low pass filter can be represented as

Note the smooth curve transition, due to which at each point, the value of Do , can be exactly defined.

Gaussian high pass filter

Gaussian high pass filter has the same concept as ideal high pass filter , but again the transition is more smooth as compared to the ideal one.

In this tutorial, we are going to talk about color spaces.

What are color spaces?

Color spaces are different types of color modes, used in image processing and signals and system for various purposes. Some of the common color spaces are:

• RGB

• CMY’K

• Y’UV

• YIQ

• Y’CbCr

• HSV

RGB

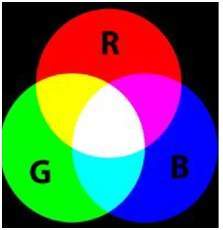
RGB is the most widely used color space , and we have already discussed it in the past tutorials. RGB stands for red green and blue.

What RGB model states , that each color image is actually formed of three different images. Red image , Blue image , and black image. A normal grayscale image can be defined by only one matrix, but a color image is actually composed of three different matrices.

One color image matrix = red matrix + blue matrix + green matrix

This can be best seen in this example below.

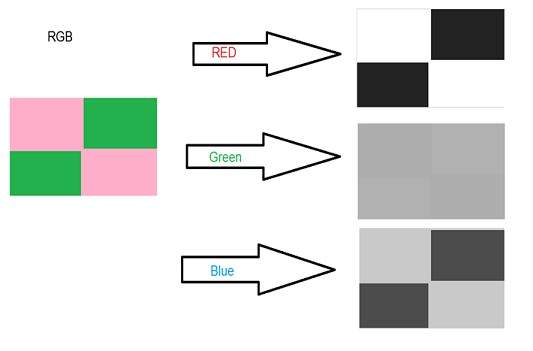
Applications of RGB

The common applications of RGB model are

• Cathode ray tube (CRT)

• Liquid crystal display (LCD)

• Plasma Display or LED display such as a television

• A compute monitor or a large scale screen

CMYK

RGB to CMY conversion

The conversion from RGB to CMY is done using this method.

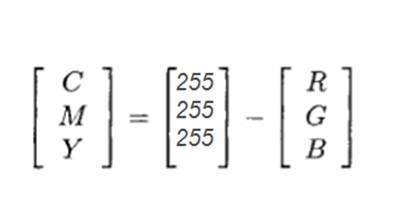
Consider you have an color image , means you have three different arrays of RED , GREEN and BLUE. Now if you want to convert it into CMY , here’s what you have to do. You have to subtract it by the maximum number of levels – 1. Each matrix is subtracted and its respective CMY matrix is filled with result.

Y’UV

Y’UV defines a color space in terms of one luma (Y’) and two chrominance (UV) components. The Y’UV color model is used in the following composite color video standards.

• NTSC ( National Television System Committee)

• PAL (Phase Alternating Line)

• SECAM (Sequential couleur a amemoire, French for “sequential color with memory)

Y’CbCr

Y’CbCr color model contains Y’ , the luma component and cb and cr are the blue-differnece and red difference chroma components.

It is not an absolute color space. It is mainly used for digital systems

Suas aplicações comuns incluem compressão JPEG e MPEG.

Y'UV é freqüentemente usado como o termo para Y'CbCr, no entanto, eles são formatos totalmente diferentes. A principal diferença entre os dois é que o primeiro é analógico, enquanto o último é digital.

Em nosso último tutorial de compressão de imagem, discutimos algumas das técnicas usadas para compressão

Vamos discutir a compactação JPEG, que é uma compactação com perdas, já que alguns dados são perdidos no final.

Vamos discutir primeiro o que é compactação de imagem.

Compressão de imagem

A compressão de imagem é o método de compressão de dados em imagens digitais.

O objetivo principal na compressão da imagem é:

• Armazene dados de forma eficiente

• Transmita dados de forma eficiente

A compressão da imagem pode ser com ou sem perdas.

Compressão JPEG

JPEG significa Joint photographic experts group. É o primeiro padrão interanacional em compressão de imagens. É amplamente utilizado hoje. Pode ser tanto com perdas quanto sem perdas. Mas a técnica que vamos discutir aqui hoje é a técnica de compressão com perdas.

Como funciona a compactação jpeg:

O primeiro passo é dividir uma imagem em blocos com cada um tendo dimensões de 8 x 8.

Vamos para o registro, digamos que esta imagem 8x8 contenha os seguintes valores.

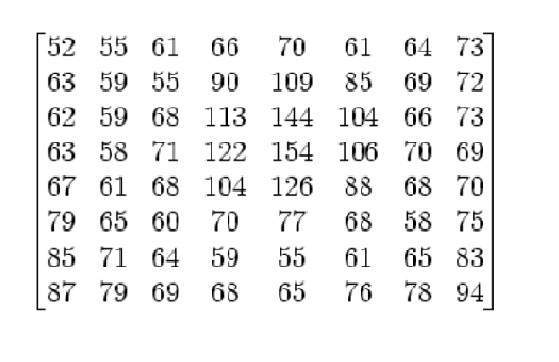
A faixa de intensidades de pixels agora é de 0 a 255. Iremos alterar a faixa de -128 a 127.

Subtraindo 128 de cada valor de pixel produz o valor de pixel de -128 a 127. Depois de subtrair 128 de cada valor de pixel, obtivemos os seguintes resultados.

Agora vamos calcular usando esta fórmula.

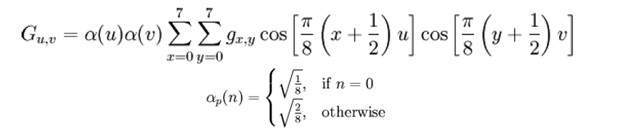
O resultado vem disso é armazenado em uma matriz, digamos A (j, k).

Existe uma matriz padrão que é usada para calcular a compressão JPEG, que é fornecida por uma matriz chamada matriz de luminância.

Esta matriz é dada abaixo

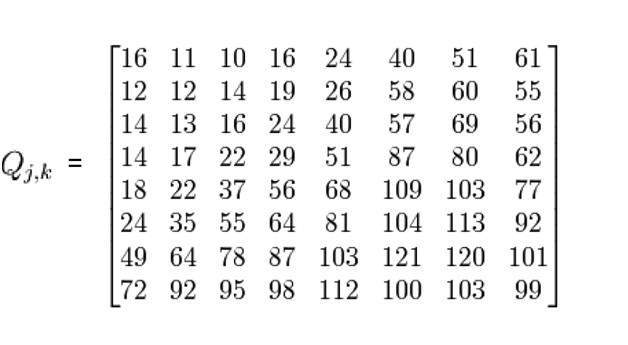
Aplicando a seguinte fórmula

Obtivemos esse resultado após a aplicação.

Agora vamos realizar o truque real que é feito na compressão JPEG, que é o movimento ZIG-ZAG. A seqüência de ziguezague para a matriz acima é mostrada abaixo. Você deve executar o zig zag até encontrar todos os zeros à frente. Portanto, nossa imagem agora está compactada.

Summarizing JPEG compression

O primeiro passo é converter uma imagem em Y'CbCr e apenas escolher o canal Y 'e dividi-la em blocos de 8 x 8. Então, começando do primeiro bloco, mapeie o intervalo de -128 a 127. Depois disso, você deve encontrar a transformada de Fourier discreta da matriz. O resultado disso deve ser quantizado. A última etapa é aplicar a codificação em zigue-zague e fazer isso até encontrar zero.

Salve esta matriz unidimensional e pronto.

Note. You have to repeat this procedure for all the block of 8 x 8.

O reconhecimento óptico de caracteres geralmente é abreviado como OCR. Inclui a conversão mecânica e elétrica de imagens digitalizadas de texto manuscrito e datilografado em texto de máquina. É um método comum de digitalização de textos impressos para que possam ser pesquisados ​​eletronicamente, armazenados de forma mais compacta, exibidos on-line e usados ​​em processos de máquina, como tradução automática, texto em fala e mineração de texto.

Nos últimos anos, a tecnologia OCR (Optical Character Recognition) tem sido aplicada em todo o espectro de indústrias, revolucionando o processo de gerenciamento de documentos. O OCR permitiu que documentos digitalizados se tornassem mais do que apenas arquivos de imagem, transformando-se em documentos totalmente pesquisáveis ​​com conteúdo de texto reconhecido por computadores. Com a ajuda do OCR, as pessoas não precisam mais redigitar manualmente documentos importantes ao inseri-los em bancos de dados eletrônicos. Em vez disso, o OCR extrai informações relevantes e as insere automaticamente. O resultado é um processamento de informações preciso e eficiente em menos tempo.

O reconhecimento óptico de caracteres tem várias áreas de pesquisa, mas as áreas mais comuns são as seguintes:

Banking:

Os usos do OCR variam em diferentes campos. Uma aplicação amplamente conhecida é no setor bancário, onde OCR é usado para processar cheques sem envolvimento humano. Um cheque pode ser inserido em uma máquina, a escrita nele é digitalizada instantaneamente e a quantia correta de dinheiro é transferida. Essa tecnologia foi quase aperfeiçoada para cheques impressos e é bastante precisa também para cheques manuscritos, embora às vezes exija confirmação manual. No geral, isso reduz o tempo de espera em muitos bancos.

Blind and visually impaired persons:

Um dos principais fatores no início da pesquisa por trás do OCR é que os cientistas querem fazer um computador ou dispositivo que possa ler livros para pessoas cegas em voz alta. Nesta pesquisa, o cientista fez um scanner de mesa que é mais comumente conhecido por nós como scanner de documentos.

Legal department:

No setor jurídico, também houve um movimento significativo para digitalizar documentos em papel. Para economizar espaço e eliminar a necessidade de vasculhar caixas de arquivos em papel, os documentos estão sendo digitalizados e inseridos em bancos de dados de computador. O OCR simplifica ainda mais o processo, tornando os documentos pesquisáveis ​​por texto, para que sejam mais fáceis de localizar e trabalhar uma vez no banco de dados. Profissionais jurídicos agora têm acesso rápido e fácil a uma enorme biblioteca de documentos em formato eletrônico, que podem encontrar simplesmente digitando algumas palavras-chave.

Retail Industry:

A tecnologia de reconhecimento de código de barras também está relacionada ao OCR. Vemos o uso dessa tecnologia em nosso uso diário comum.

Other Uses:

OCR é amplamente utilizado em muitos outros campos, incluindo educação, finanças e agências governamentais. O OCR disponibiliza inúmeros textos online, economizando dinheiro para os alunos e permitindo que o conhecimento seja compartilhado. Os aplicativos de geração de imagens de faturas são usados ​​em muitas empresas para controlar os registros financeiros e evitar o acúmulo de pagamentos em atraso. Em agências governamentais e organizações independentes, o OCR simplifica a coleta e análise de dados, entre outros processos. À medida que a tecnologia continua a se desenvolver, mais e mais aplicativos são encontrados para a tecnologia OCR, incluindo maior uso de reconhecimento de manuscrito.

Visão Computacional

A visão computacional se preocupa com a modelagem e a replicação da visão humana usando software e hardware de computador. Formalmente, se definirmos visão computacional, então sua definição seria que a visão computacional é uma disciplina que estuda como reconstruir, interromper e compreender uma cena 3D a partir de suas imagens 2D em termos das propriedades da estrutura presente na cena.

Necessita de conhecimento das seguintes áreas, a fim de compreender e estimular o funcionamento do sistema de visão humana.

• Ciência da Computação

• Engenharia elétrica

• Mathematics

• Physiology

• Biology

• Ciência cognitiva

Hierarquia de visão computacional:

A visão computacional é dividida em três categorias básicas que são as seguintes:

Visão de baixo nível: inclui imagem de processo para extração de recursos.

Visão de nível intermediário: inclui reconhecimento de objeto e interpretação de cena 3D

Visão de alto nível: inclui a descrição conceitual de uma cena como atividade, intenção e comportamento.

Campos relacionados:

A visão computacional se sobrepõe significativamente aos seguintes campos:

Processamento de imagens: enfoca a manipulação de imagens.

Reconhecimento de padrões: estuda várias técnicas de classificação de padrões.

Fotogrametria: preocupa-se em obter medidas precisas de imagens.

Visão computacional versus processamento de imagem:

O processamento de imagens estuda a transformação de imagem em imagem. A entrada e a saída do processamento de imagem são imagens.

A visão computacional é a construção de descrições explícitas e significativas de objetos físicos a partir de sua imagem. A saída da visão computacional é uma descrição ou interpretação de estruturas em cena 3D.

Aplicativos de exemplo:

• Robotics

• Medicine

• Security

• Transportation

• Automação industrial

Aplicação de robótica:

• Localização - determina a localização do robô automaticamente

• Navigation

• Evitar obstáculos

• Montagem (peg-in-hole, soldagem, pintura)

• Manipulação (por exemplo, robô manipulador PUMA)

• Human Robot Interaction (HRI): robótica inteligente para interagir e servir as pessoas

Aplicação de medicamento:

• Classificação e detecção (por exemplo, lesão ou classificação de células e detecção de tumor)

• Segmentação 2D / 3D

• Reconstrução 3D de órgãos humanos (ressonância magnética ou ultrassom)

• Cirurgia robótica guiada pela visão

Aplicação de automação industrial:

• Inspeção industrial (detecção de defeito)

• Assembly

• Leitura do código de barras e etiqueta da embalagem

• Classificação de objetos

• Compreensão de documentos (por exemplo, OCR)

Aplicação de segurança:

• Biometria (íris, impressão digital, reconhecimento facial)

• Vigilância - detecção de certas atividades ou comportamentos suspeitos

Aplicação de transporte:

• Veículo autônomo

• Segurança, por exemplo, monitoramento de vigilância do motorista

Computação Gráfica

Os gráficos de computador são gráficos criados usando computadores e a representação de dados de imagem por um computador especificamente com a ajuda de hardware e software gráfico especializado. Formalmente, podemos dizer que Computação Gráfica é criação, manipulação e armazenamento de objetos geométricos (modelagem) e suas imagens (Rendering).

O campo da computação gráfica se desenvolveu com o surgimento do hardware de computação gráfica. Hoje, a computação gráfica é usada em quase todos os campos. Muitas ferramentas poderosas foram desenvolvidas para visualizar dados. O campo da computação gráfica se tornou mais popular quando as empresas começaram a usá-lo em videogames. Hoje é uma indústria multibilionária e a principal força motriz por trás do desenvolvimento de computação gráfica. Algumas áreas de aplicativos comuns são as seguintes:

• Design Assistido por Computador (CAD)

• Apresentação Gráfica

• Animação 3D

• Educação e treinamento

• Interfaces Gráficas do Usuário

Projeto auxiliado por computador:

• Usado em projetos de edifícios, automóveis, aeronaves e muitos outros produtos

• Use para fazer sistema de realidade virtual.

Gráficos de apresentação:

• Normalmente usado para resumir dados financeiros e estatísticos

• Use para gerar slides

Animação 3D:

• Muito usado na indústria cinematográfica por empresas como Pixar, DresmsWorks

• Para adicionar efeitos especiais em jogos e filmes.

Educação e treinamento:

• Modelos de sistemas físicos gerados por computador

• Visualização Médica

• Ressonância magnética 3D

• Exames dentários e ósseos

• Estimuladores para treinamento de pilotos etc.

Interfaces gráficas do usuário:

• É usado para fazer objetos de interface gráfica do usuário como botões, ícones e outros componentes