Финансовый анализ данных Excel
Вы можете легко выполнять финансовый анализ с помощью Excel. Excel предоставляет вам несколько финансовых функций, таких как PMT, PV, NPV, XNPV, IRR, MIRR, XIRR и т. Д., Которые позволяют быстро получить результаты финансового анализа.
В этой главе вы узнаете, где и как можно использовать эти функции для анализа.
Что такое аннуитет?
Аннуитет - это серия постоянных денежных выплат, производимых в течение непрерывного периода. Например, накопления на пенсию, страховые выплаты, жилищный заем, ипотека и т. Д. В функциях аннуитета -
- Положительное число представляет собой полученные денежные средства.
- Отрицательное число означает выплату наличных.
Текущая стоимость серии будущих платежей
Приведенная стоимость - это общая сумма, которую сейчас стоит серия будущих платежей. Вы можете рассчитать приведенную стоимость с помощью функций Excel -
PV- Рассчитывает приведенную стоимость инвестиции с использованием процентной ставки и ряда будущих платежей (отрицательные значения) и дохода (положительные значения). По крайней мере один из денежных потоков должен быть положительным и хотя бы один должен быть отрицательным.
NPV - Рассчитывает чистую приведенную стоимость инвестиции с использованием ставки дисконтирования и серии периодических будущих платежей (отрицательные значения) и дохода (положительные значения).
XNPV - Рассчитывает чистую приведенную стоимость для графика денежных потоков, который не обязательно является периодическим.
Note that -
Денежные потоки PV должны быть постоянными, тогда как денежные потоки NPV могут быть переменными.
Денежные потоки PV могут быть в начале или в конце периода, тогда как денежные потоки NPV должны быть в конце периода.
Денежные потоки NPV должны быть периодическими, тогда как денежные потоки XNPV не должны быть периодическими.
В этом разделе вы поймете, как работать с PV. Вы узнаете о NPV в следующем разделе.
пример
Предположим, вы покупаете холодильник. Продавец сообщает вам, что цена холодильника 32000, но у вас есть возможность выплатить эту сумму через 8 лет с процентной ставкой 13% годовых и ежегодными платежами в размере 6000. У вас также есть возможность производить платежи. либо в начале, либо в конце каждого года.
Вы хотите знать, какой из этих вариантов вам подходит.
Вы можете использовать функцию Excel PV -
PV (rate, nper, pmt, [fv ], [type])Чтобы рассчитать приведенную стоимость с выплатами в конце каждого года, опустите тип или укажите 0 в качестве типа.
Чтобы рассчитать приведенную стоимость с выплатами в конце каждого года, укажите 1 для типа.

Вы получите следующие результаты -

Следовательно,
- Если вы произведете оплату сейчас, вам нужно будет заплатить 32 000 от текущей стоимости.
- Если вы выберете ежегодные платежи с оплатой в конце года, вам необходимо заплатить 28 793 приведенной стоимости.
- Если вы выберете ежегодные платежи с оплатой в конце года, вам нужно будет заплатить 32 536 от текущей стоимости.
Вы можете ясно видеть, что вариант 2 выгоден для вас.
Что такое EMI?
Выравниваемый ежемесячный платеж (EMI) определяется Investopedia как «фиксированная сумма платежа, производимая заемщиком кредитору в указанную дату каждый календарный месяц. Уравненные ежемесячные платежи используются для выплаты как процентов, так и основной суммы каждый месяц, чтобы через указанное количество лет ссуда выплачивается полностью ».
EMI в ссуде
В Excel вы можете рассчитать EMI по ссуде с помощью функции PMT.
Допустим, вы хотите взять жилищный заем в размере 5000000 с годовой процентной ставкой 11,5% и сроком кредита на 25 лет. Вы можете найти свой EMI следующим образом -
- Рассчитайте процентную ставку в месяц (процентная ставка в год / 12)
- Рассчитать количество ежемесячных платежей (Кол-во лет * 12)
- Используйте функцию PMT для расчета EMI

Как вы заметили,
- Текущая стоимость (PV) - это сумма кредита.
- Будущая стоимость (FV) равна 0, так как в конце срока сумма кредита должна быть 0.
- Тип - 1, так как EMI выплачиваются в начале каждого месяца.
Вы получите следующие результаты -

Ежемесячный платеж основной суммы и процентов по ссуде
EMI включает как проценты, так и частичную выплату основной суммы долга. По мере увеличения времени эти два компонента EMI будут изменяться, уменьшая баланс.
Получить
Процентную часть ваших ежемесячных платежей вы можете использовать с помощью функции Excel IPMT.
Для оплаты основной части ваших ежемесячных платежей вы можете использовать функцию Excel PPMT.
Например, если вы взяли ссуду в размере 1 000 000 на срок 8 месяцев по ставке 16% годовых. Вы можете получить значения EMI, уменьшающихся сумм процентов, увеличивающихся выплат основной суммы и уменьшающегося остатка кредита в течение 8 месяцев. По истечении 8 месяцев остаток по кредиту будет равен 0.
Следуйте процедуре, приведенной ниже.
Step 1 - Рассчитайте EMI следующим образом.

Это приводит к EMI рупий. 13261,59.

Step 2 - Затем рассчитайте процентную и основную часть EMI за 8 месяцев, как показано ниже.

Вы получите следующие результаты.

Выплата процентов и основной суммы в период между двумя периодами
Вы можете вычислить проценты и основную сумму, выплаченные между двумя периодами включительно.
Вычислите совокупные проценты, выплаченные между 2- м и 3- м месяцами, с помощью функции CUMIPMT.
Проверить результат, суммируя значения процентов за 2- й и 3- й месяц.
Рассчитайте совокупную основную сумму, выплаченную между 2- м и 3- м месяцами, с помощью функции CUMPRINC.
Проверьте результат , заключающий главные значения для 2 - го и 3 - го месяца.

Вы получите следующие результаты.

Вы можете видеть, что ваши расчеты совпадают с результатами проверки.
Расчет процентной ставки
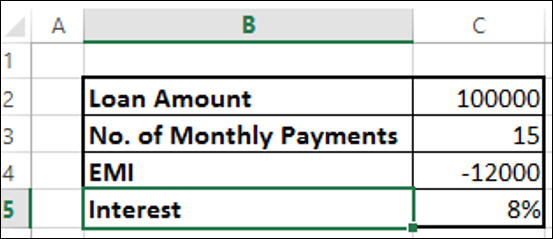
Предположим, вы берете ссуду в размере 100 000 и хотите выплатить ее в течение 15 месяцев с максимальным ежемесячным платежом в 12 000. Возможно, вы захотите узнать процентную ставку, по которой вы должны платить.
Найдите процентную ставку с помощью функции Excel RATE -

Вы получите результат 8%.
Расчет срока кредита
Допустим, вы берете ссуду на сумму 100 000 под процентную ставку 10%. Вам нужен максимальный ежемесячный платеж в размере 15000. Возможно, вы захотите узнать, сколько времени вам понадобится, чтобы погасить ссуду.
Найдите количество платежей с помощью функции Excel NPER

Результат будет через 12 месяцев.

Решения по инвестициям
Если вы хотите инвестировать, вы сравниваете различные варианты и выбираете тот, который приносит больше прибыли. Чистая приведенная стоимость полезна для сравнения денежных потоков за определенный период времени и принятия решения о том, какой из них лучше. Денежные потоки могут происходить с регулярными, периодическими интервалами или нерегулярными интервалами.
Сначала рассмотрим случай regular, periodical cash flows.
Чистая приведенная стоимость последовательности денежных потоков, полученных в разные моменты времени через n лет (n может быть дробью), равна 1/(1 + r)n, где r - годовая процентная ставка.
Рассмотрим следующие две инвестиции в течение 3 лет.
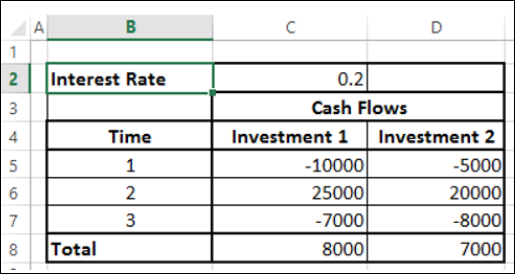
На первый взгляд, инвестиция 1 выглядит лучше, чем инвестиция 2. Однако вы можете решить, какая инвестиция лучше, только если вы знаете истинную стоимость инвестиций на сегодняшний день. Вы можете использовать функцию NPV для расчета прибыли.
Денежные потоки могут возникать
- В конце каждого года.
- В начале каждого года.
- В середине каждого года.
Функция NPV предполагает, что денежные потоки приходятся на конец года. Если денежные потоки происходят в разное время, вы должны принять во внимание этот конкретный фактор вместе с расчетом с использованием NPV.
Предположим, денежные потоки происходят в конце года. Тогда вы можете сразу использовать функцию NPV.
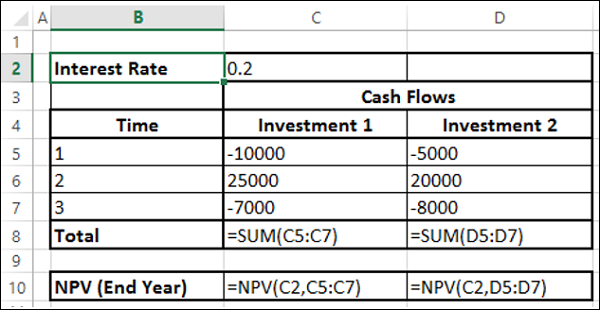
Вы получите следующие результаты -

Как вы видите, NPV для инвестиции 2 выше, чем для инвестиции 1. Следовательно, инвестиция 2 - лучший выбор. Вы получили этот результат, так как потоки денежных средств для инвестиции 2 находятся в более поздних периодах по сравнению с потоком денежных средств для инвестиции 1.
Денежные потоки на начало года
Предположим, денежные потоки возникают в начале каждого года. В таком случае вы не должны включать первый денежный поток в расчет NPV, поскольку он уже представляет текущее значение. Чтобы получить чистую приведенную стоимость, вам нужно добавить первый денежный поток к чистой приведенной стоимости, полученной от остальных денежных потоков.

Вы получите следующие результаты -

Денежные потоки в середине года
Предположим, денежные потоки возникают в середине каждого года. В таком случае вам нужно умножить NPV, полученную от денежных потоков, на $ \ sqrt {1 + r} $, чтобы получить чистую приведенную стоимость.

Вы получите следующие результаты -

Денежные потоки с нерегулярными интервалами
Если вы хотите рассчитать чистую приведенную стоимость с нерегулярными денежными потоками, то есть денежными потоками, возникающими в случайные моменты времени, расчет будет немного сложным.
Однако в Excel вы можете легко выполнить такой расчет с помощью функции XNPV.
- Организуйте свои данные с указанием дат и денежных потоков.
Note- Первая дата в ваших данных должна быть самой ранней из всех дат. Остальные даты могут встречаться в любом порядке.
- Используйте функцию XNPV для расчета чистой приведенной стоимости.
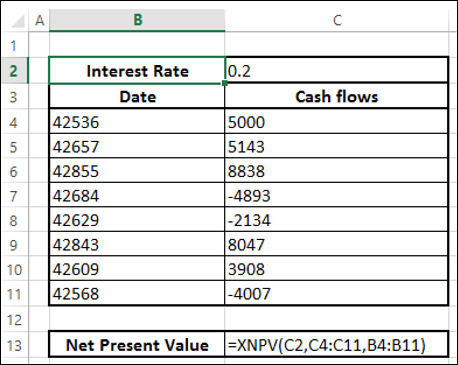
Вы получите следующие результаты -

Предположим , что текущая дата 15 - го марта 2015 г. Как вы заметили, все даты потоков денежных средств в более поздние сроки. Если вы хотите найти чистую приведенную стоимость на сегодняшний день, включите ее в данные вверху и укажите 0 для денежного потока.

Вы получите следующие результаты -

Внутренняя норма доходности (IRR)
Внутренняя норма доходности (IRR) инвестиций - это процентная ставка, при которой NPV равна 0. Это значение ставки, при котором текущие значения положительных денежных потоков в точности компенсируют отрицательные. Когда ставкой дисконтирования является IRR, вложения совершенно безразличны, то есть инвестор не получает и не теряет деньги.
Рассмотрим следующие денежные потоки, различные процентные ставки и соответствующие значения NPV.

Как вы можете заметить, между значениями процентной ставки 10% и 11% знак NPV меняется. Когда вы настраиваете процентную ставку на 10,53%, NPV составляет почти 0. Следовательно, IRR составляет 10,53%.
Определение IRR денежных потоков по проекту
Вы можете рассчитать IRR денежных потоков с помощью функции Excel IRR.

IRR составляет 10,53%, как вы видели в предыдущем разделе.
Для данных денежных потоков IRR может:
- существуют и уникальны
- существуют и множественные
- не существует
Уникальный IRR
Если IRR существует и уникален, его можно использовать для выбора наилучшего вложения из нескольких возможных.
Если первый денежный поток отрицательный, это означает, что у инвестора есть деньги и он хочет инвестировать. Тогда чем выше IRR, тем лучше, поскольку она представляет процентную ставку, которую получает инвестор.
Если первый денежный поток положительный, это означает, что инвестору нужны деньги и он ищет ссуду. Чем ниже IRR, тем лучше, поскольку она представляет собой процентную ставку, которую платит инвестор.
Чтобы определить, является ли IRR уникальным или нет, измените предполагаемое значение и рассчитайте IRR. Если IRR остается постоянным, то он уникален.

Как вы заметили, IRR имеет уникальное значение для разных предполагаемых значений.

Множественные IRR
В некоторых случаях у вас может быть несколько IRR. Рассмотрим следующие денежные потоки. Рассчитайте IRR с различными предполагаемыми значениями.

Вы получите следующие результаты -

Вы можете заметить, что существует две IRR - -9,59% и 216,09%. Вы можете проверить эти две IRR, вычислив NPV.

И для -9,59%, и для 216,09% ЧПС равно 0.
Нет IRR
В некоторых случаях у вас может не быть IRR. Рассмотрим следующие денежные потоки. Рассчитайте IRR с различными предполагаемыми значениями.

Вы получите результат как # ЧИСЛО для всех предполагаемых значений.

Результат # ЧИСЛО означает, что IRR для рассматриваемых денежных потоков отсутствует.
Модели денежных потоков и IRR
Если в денежных потоках меняется только один знак, например, с отрицательного на положительный или с положительного на отрицательный, то гарантируется уникальная внутренняя норма доходности. Например, при капитальных вложениях первый денежный поток будет отрицательным, а остальные денежные потоки будут положительными. В таких случаях существует уникальный IRR.
Если в денежных потоках происходит более одного изменения знака, IRR может не существовать. Даже если он существует, он не может быть уникальным.
Решения на основе IRR
Многие аналитики предпочитают использовать IRR, и это популярный показатель рентабельности, потому что в процентах его легко понять и легко сравнить с требуемой доходностью. Однако есть определенные проблемы при принятии решений с IRR. Если вы оцениваете IRR и принимаете решения на основе этих рейтингов, вы можете принять неправильные решения.
Вы уже видели, что NPV позволит вам принимать финансовые решения. Однако IRR и NPV не всегда приводят к одному и тому же решению, когда проекты являются взаимоисключающими.
Mutually exclusive projectsэто те проекты, для которых выбор одного проекта исключает принятие другого. Когда сравниваемые проекты являются взаимоисключающими, может возникнуть конфликт ранжирования между NPV и IRR. Если вам нужно выбрать между проектом A и проектом B, NPV может предложить принятие проекта A, тогда как IRR может предложить проект B.
Этот тип конфликта между NPV и IRR может возникнуть по одной из следующих причин:
- Проекты бывают самых разных размеров, или
- Сроки денежных потоков разные.
Проекты значительной разницы в размерах
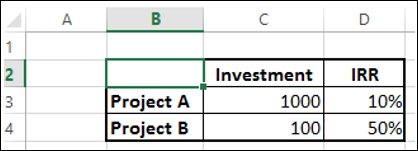
Если вы хотите принять решение по IRR, проект A даст доходность 100, а проект B - 50. Следовательно, инвестиции в проект A выглядят прибыльными. Однако это неправильное решение из-за разницы в масштабах проектов.
Учтите -
У вас есть 1000 для инвестирования.
Если вы инвестируете целые 1000 долларов в проект А, вы получите 100 прибыли.
Если вы инвестируете 100 в проект B, у вас все равно будет 900 в ваших руках, которые вы можете инвестировать в другой проект, скажем, в проект C. Предположим, вы получаете доходность 20% по проекту C, тогда общая прибыль по проекту B и проекту C составляет 230, что намного выше по рентабельности.
Таким образом, NPV - лучший способ принятия решений в таких случаях.
Проекты с разными сроками движения денежных средств

Опять же, если вы рассматриваете IRR, чтобы решить, проект B будет выбором. Однако проект A имеет более высокую NPV и является идеальным выбором.
IRR нерегулярных денежных потоков (XIRR)
Иногда ваши денежные потоки могут быть неравномерными. В таком случае вы не можете использовать IRR, поскольку IRR требует равных интервалов времени. Вместо этого вы можете использовать XIRR, который учитывает даты денежных потоков вместе с денежными потоками.

Полученная в результате внутренняя норма доходности составляет 26,42%.

Модифицированная IRR (MIRR)
Рассмотрим случай, когда ваша ставка финансирования отличается от ставки реинвестирования. Если вы рассчитываете внутреннюю норму прибыли с помощью IRR, предполагается, что она одинакова как для финансирования, так и для реинвестирования. Кроме того, вы также можете получить несколько IRR.
Например, рассмотрим денежные потоки, приведенные ниже -

Как вы заметили, NPV больше одного раза равна 0, что приводит к множеству IRR. Далее не учитывается ставка реинвестирования. В таких случаях вы можете использовать модифицированный IRR (MIRR).

Вы получите результат 7%, как показано ниже -

Note - В отличие от IRR, MIRR всегда будет уникальным.