Сигналы Основные операции
Обычно существует два переменных параметра:
- Amplitude
- Time
The following operation can be performed with amplitude:
Масштабирование амплитуды
C x (t) представляет собой масштабированную по амплитуде версию x (t), амплитуда которой масштабируется с коэффициентом C.

Дополнение
Сложение двух сигналов есть не что иное, как сложение их соответствующих амплитуд. Лучше всего это можно объяснить на следующем примере:

Как видно из диаграммы выше,
-10 <t <-3 амплитуда z (t) = x1 (t) + x2 (t) = 0 + 2 = 2
-3 <t <3 амплитуда z (t) = x1 (t) + x2 (t) = 1 + 2 = 3
3 <t <10 амплитуда z (t) = x1 (t) + x2 (t) = 0 + 2 = 2
Вычитание
вычитание двух сигналов есть не что иное, как вычитание их соответствующих амплитуд. Лучше всего это можно объяснить на следующем примере:

Как видно из диаграммы выше,
-10 <t <-3 амплитуда z (t) = x1 (t) - x2 (t) = 0-2 = -2
-3 <t <3 амплитуда z (t) = x1 (t) - x2 (t) = 1-2 = -1
3 <t <10 амплитуда z (t) = x1 (t) + x2 (t) = 0-2 = -2
Умножение
Умножение двух сигналов есть не что иное, как умножение соответствующих им амплитуд. Лучше всего это можно объяснить на следующем примере:
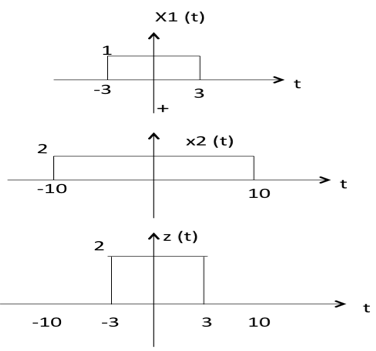
Как видно из диаграммы выше,
-10 <t <-3 амплитуда z (t) = x1 (t) × x2 (t) = 0 × 2 = 0
-3 <t <3 амплитуда z (t) = x1 (t) × x2 (t) = 1 × 2 = 2
3 <t <10 амплитуда z (t) = x1 (t) × x2 (t) = 0 × 2 = 0
Временной сдвиг
x (t $ \ pm $ t 0 ) - это версия сигнала x (t) со сдвигом во времени.
x (t + t 0 ) $ \ to $ отрицательный сдвиг
x (t - t 0 ) $ \ to $ положительный сдвиг

Масштабирование времени
x (At) - масштабированная по времени версия сигнала x (t). где A всегда положительно.
| A | > 1 $ \ to $ Сжатие сигнала
| A | <1 $ \ to $ Расширение сигнала

Примечание: u (at) = u (t) масштабирование времени не применимо для функции единичного шага.
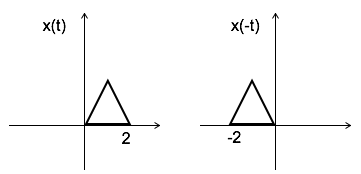
Обратное время
x (-t) - обращение времени сигнала x (t).